1. Правая часть

а) Тогда, если α – не является корнем характеристического уравнения α ≠ k₁ и α ≠ k₂, то

y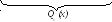_частн. = Q_n(x)*e ^αx = (b₀ + b₁x + b₂x² + . . . + b_nxⁿ)*e ^αx .

б) Если α – один из корней характеристического уравнения α = k₁ и α ≠ k₂, то

y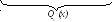_частн. = Q_n(x)*x*e ^αx = (b₀ + b₁x + b₂x² + . . . + b_nxⁿ)*x*e ^αx .

в) Если α = k₁ = k₂, то

y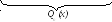_частн. = Q_n(x)*x²*e ^αx = (b₀ + b₁x + b₂x² + . . . + b_nxⁿ)*x²*e ^αx .

Многочлен Q_n (x) (его коэффициенты b₀, b₁, b₂ . . . b_n) находят методом неопределённых коэффициентов.

2. Правая часть

а) Если k₁≠ 0 и k₂ ≠ 0, то

y_частн. = Q_n(x) = (b₀ + b₁x + b₂x² + . . . + b_nxⁿ) .

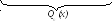
б) Если k₁= 0 и k₁ ≠ k₂, то

y_частн. = x*Q_n(x) = x*(b₀ + b₁x + b₂x² + . . . + b_nxⁿ) .

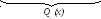
в) Если k₁= k₂ = 0, то

y_частн. = x²*Q_n(x) =x²* (b₀ + b₁x + b₂x² + . . . + b_nxⁿ) .

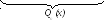
Многочлен Q_n (x) (его коэффициенты b₀, b₁, b₂ . . . b_n) находят методом неопределённых коэффициентов.

3. П

   f(x) = e ^αx * (A*cosβx + B*sinβx)

   равая часть

а) Если α ± βi не являются корнями характеристического уравнения, то

y_частн.= e ^αx * (M*cosβx + N*sinβx).

б) Если α ± βi являются корнями характеристического уравнения, то

y_частн.= x*e ^αx * (M*cosβx + N*sinβx).

M, N находят методом неопределённых коэффициентов.

4. П

   f(x) = A*cosβx + B*sinβx

   равая часть

а) Если βi не является корнем характеристического уравнения, то

y_частн.= M*cosβx + N*sinβx.

б) Если βi является корнем характеристического уравнения, то

y_частн.= x*(M*cosβx + N*sinβx).

M, N находят методом неопределённых коэффициентов.

= .

РЯДЫ

10. Числовые ряды. Определения числового ряда, частичной суммы ряда. Понятие сходящихся и расходящихся рядов.

Определение 1

Числовым рядом называется бесконечная числовая последовательность, соединенная знаком сложения.

Числа - числа числового ряда.

Ряд считается заданным, если задана формула (правило), по которой для любого номера n можно вычислить соответствующий член ряда.

- формула общего члена ряда.

Числовые и функциональные ряды находят широкое применение в различных вычислениях, когда сложную функцию представляют в виде суммы простых функций, т.к. в виде ряда.

Такой подход широко применяют в вычислительной технике.

Определение 2

Пусть задан числовой ряд , тогда выражение вида - частичные суммы ряда.

S_n – частичная сумма ряда.

Определение 3 Если для ряда существует конечный предел , то такие ряды называют сходящимися, а s – сумма ряда.

Если конечного предела таких сумм не существует, то ряд называют расходящимся.

10. Ряд, образованный из членов бесконечной геометрической прогрессии, условия его сходимости и расходимости.

Рассмотрим ряд, составленный из членов геометрической прогрессии.

Геометрическая прогрессия , b – первый член, q – знаменатель.

Ряд

Исследуем этот ряд на сходимость. Как известно, сумма первых n-членов геометр. прогрессии . Найдем Sn, когда .

, (*)

При исследовании рядов наиболее важным является вопрос о сходимости (установление факта сходимости и расходимости). Для этого используют признак сходимсоти.