
- •Дифференциальные уравнения первого порядка. Теорема существования и единственности решения. Основные понятия и определения – общее и частное решение, начальные условия, задача Коши.
- •Дифференциальные уравнения с разделяющимися переменными . Алгоритм решения.
- •Однородные дифференциальные уравнения первого порядка . Решение однородных уравнений.
- •Линейные дифференциальные уравнения первого порядка . Метод Бернулли решения линейных дифференциальных уравнений первого порядка.
- •5. Дифференциальные уравнения второго порядка, основные понятия. Уравнения второго порядка, допускающие понижение порядка вида .
- •Решение дифференциальных уравнений второго порядка, допускающих понижение порядка вида .
- •Решение дифференциальных уравнений второго порядка, допускающих понижение порядка вида .
- •Правая часть
- •Правая часть
- •Определение 1
- •Определение 2
- •Определение 3 Если для ряда существует конечный предел , то такие ряды называют сходящимися, а s – сумма ряда.
- •Ряд, образованный из членов бесконечной геометрической прогрессии, условия его сходимости и расходимости.
- •Необходимый признак сходимости числовых рядов. Свойства сходящихся рядов.
- •Признаки сравнения знакоположительных числовых рядов. Первый и второй признак сравнения.
- •Интегральный признак Коши.
- •Признак Даламбера.
- •Знакочередующиеся числовые ряды (определение, примеры). Признак Лейбница.
- •Абсолютная и условная сходимость знакочередующихся числовых рядов.
- •Степенные ряды. Теорема Абеля. Понятие области сходимости степенных рядов.
- •Алгоритм исследования степенных рядов на сходимость.
- •Ряд Маклорена. Разложение в ряд Маклорена функции .
- •Теория вероятностей
- •22. Классификация событий. Пространство элементарных событий, случайное событие. Сумма и произведение событий. Противоположное событие. Несовместные события.
- •2 События: а и в называют несовместными, если
- •23. Классическое и статистическое определение вероятности случайного события. Непосредственный подсчет вероятности событий для простейших опытов.
- •Если - конечномерное пространство элем.Событий, каждое из которых равновозможное, то вероятностью события а называется отношение числа исходов, благопрепятствующих событию а к общему числу исходов.
- •25. Теоремы сложения вероятностей для несовместных и совместных событий.
- •27. Формула полной вероятности (формула Байеса).
ПРИМЕЧАНИЯ: Этим цветом выделен материал, который может и не понадобиться при ответе на данный экзаменационный билет. А может и понадобится =)
Дифференциальные уравнения
-
Дифференциальные уравнения первого порядка. Теорема существования и единственности решения. Основные понятия и определения – общее и частное решение, начальные условия, задача Коши.
Д.у. называется уравнение, содержащее производные, функцию и независимую переменную. Порядком д.у. называется порядок наивысшей степени. Решением д.у. называется всякая функция, которая при подстановке в это уравнение обращает его в тождество.
Д.у. 1го порядка называется уравнение
![]() .
Если это уравнение можно представить
в виде
.
Если это уравнение можно представить
в виде
![]() (1), то уравнение называется уравнением,
разрешенным относительно производной.
Теорема Коши: теорема существования и
единственности:
(1), то уравнение называется уравнением,
разрешенным относительно производной.
Теорема Коши: теорема существования и
единственности:
Если в уравнении (1), функция f(x,y)
и её частная производная
![]() непрерывны
в некоторой области, содержащей т.(
непрерывны
в некоторой области, содержащей т.(![]() ),
то существует и при этом единственное
решение уравнения (1), проходящее через
данную точку.
),
то существует и при этом единственное
решение уравнения (1), проходящее через
данную точку.
Примечание! 1. Задача, в которой помимо
нахождения решения д.у. требуется найти
решение, проходящее через точку (![]() )
называются задачей КОШИ. 2. Задача Коши
формулируется след-м образом:
)
называются задачей КОШИ. 2. Задача Коши
формулируется след-м образом:
Дано: - дифференциал
![]() *
*
-
начальное условие
 **
**
Требуется: найти решение, удовлетворяющее как *, так и **.
Решение, в котором С – произвольная постоянная, называется ОБЩИМ решением.
Решения, в которых С(const) конкретизирована, называют ЧАСТНЫМИ решениями.
-
Дифференциальные уравнения с разделяющимися переменными . Алгоритм решения.
(Д.у. называется ур-м с р/п
если
![]() (1). Решение основано на следующем:
выражения, стоящие слева и справа можно
рассм-ть как дифференциалы от некоторой
функции -
(1). Решение основано на следующем:
выражения, стоящие слева и справа можно
рассм-ть как дифференциалы от некоторой
функции -
![]() ,
,
![]() ,
,
![]() .
Если диф-ы ф-и равны, то сами ф-и отличаются
на С. Чтобы найти сами ф-и по диф-у их
необходимо проинтегрировать.
.
Если диф-ы ф-и равны, то сами ф-и отличаются
на С. Чтобы найти сами ф-и по диф-у их
необходимо проинтегрировать.
![]() ,
,
![]() .
Поэтому уравнение (1) решают интегрированием
обеих частей. Если в полученном решении
у явно не выражен через х или это трудно
сделать, то решение в таком виде называют
общим интегралом.)
.
Поэтому уравнение (1) решают интегрированием
обеих частей. Если в полученном решении
у явно не выражен через х или это трудно
сделать, то решение в таком виде называют
общим интегралом.)
Д.у. вида
![]() (2) называют ур-м с разделяющимися
переменными. Решение таких уравнений:
1)
(2) называют ур-м с разделяющимися
переменными. Решение таких уравнений:
1)
![]() записываем
как
записываем
как
![]() ,
,![]() ,
,
![]() - ур-е с р/п; 2) интегрируем обе части этого
равенства
- ур-е с р/п; 2) интегрируем обе части этого
равенства
![]()
![]()
![]()
![]() -
общее решение.
-
общее решение.
-
Однородные дифференциальные уравнения первого порядка . Решение однородных уравнений.
Если д.у. можно представить в виде
![]() (1), то его называют однородным. Термин
«однородность» связан с понятием так
называемых однородных функций f(x,y),
таких что
(1), то его называют однородным. Термин
«однородность» связан с понятием так
называемых однородных функций f(x,y),
таких что
![]() .
Для решения таких уравнений используют
замену переменной (подстановку). Чтобы
решить, обозначают
.
Для решения таких уравнений используют
замену переменной (подстановку). Чтобы
решить, обозначают
![]() ,
тогда
,
тогда
![]() .
Получ. выражение подставляем в исходное
(1). Интегрируем обе части. Найдем u
= F(x,С) или
.
Получ. выражение подставляем в исходное
(1). Интегрируем обе части. Найдем u
= F(x,С) или
![]() -
общее решение.
-
общее решение.
-
Линейные дифференциальные уравнения первого порядка . Метод Бернулли решения линейных дифференциальных уравнений первого порядка.
Линейным д.у.1порядка называют ур-я вида
![]() (1), где P(x),
Q(x) –
известные и непрерывные функции.
(1), где P(x),
Q(x) –
известные и непрерывные функции.
-
Если P(x)=0
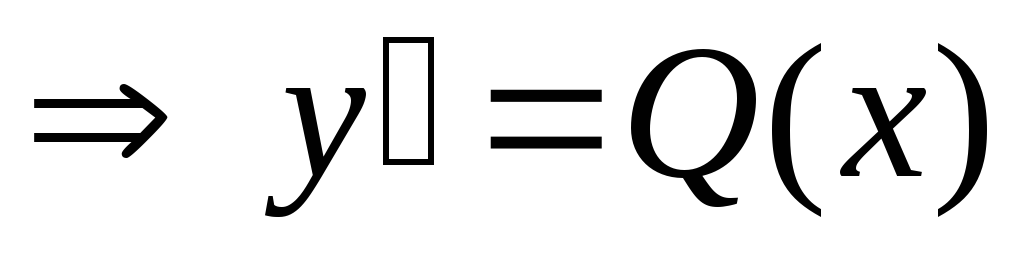 -
ур-е с разделяющимися переменными.
-
ур-е с разделяющимися переменными.
![]()
-
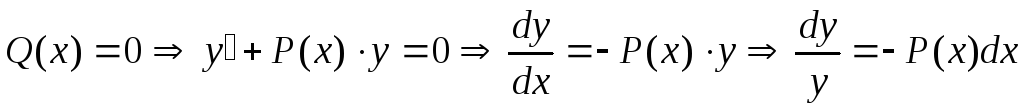 ,
Интегрируем обе части:
,
Интегрируем обе части:
 ;
;
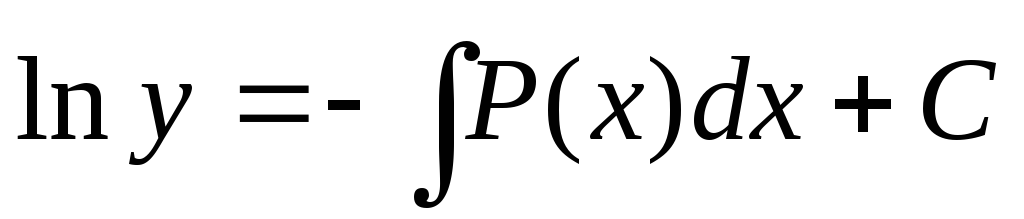
-
 - ПОЛНОЕ уравнение.
- ПОЛНОЕ уравнение.
Для решения полных уравнений используют два метода
-
метод вариации произвольной постоянной
-
метод Бернулли.
Суть метода БЕРНУЛЛИ закл.в том, что
искомое решение ищут в виде произведения
двух заранее неизвестных функций,
полагая что
![]() ,
где u и v –
пока нам неизвестные функции. Тогда
,
где u и v –
пока нам неизвестные функции. Тогда
![]() .
Подставляем в исх-е уравнение y
и
.
Подставляем в исх-е уравнение y
и
![]() ,
получаем
,
получаем
![]() *
*
Так как нас интересует результат
![]() ,
а не отдельные сомножители, то на один
их них можно наложить какое-либо условие.
Пусть будет таким, что
,
а не отдельные сомножители, то на один
их них можно наложить какое-либо условие.
Пусть будет таким, что
![]() .
Тогда,
.
Тогда,
![]()
![]()
![]() (const при нахождении полагают
равной 0).
(const при нахождении полагают
равной 0).
Подставляем найденное V
в уравнение *, тогда
![]() .
.
![]()
![]()
![]() .
.
Окончательное решение:
![]()
