
- •Раздел 1 элементы линейной алгебры и аналитической геометрии
- •Контрольные вопросы
- •1.1. Элементы линейной алгебры
- •1.2. Действия над векторами
- •1.3. Прямая на плоскости
- •1.4. Кривые второго порядка
- •1.5. Прямая в пространстве и плоскость
- •Контрольные задания по теме "Элементы линейной алгебры"
- •Контрольные задания по теме " Действия над векторами"
- •Контрольные задания по теме "Кривые второго порядка"
- •Контрольные задания по теме "Прямая в пространстве и плоскость"
- •Раздел 2 Пределы и непрерывность функции
- •Контрольные вопросы
- •Контрольные задания по теме "Пределы и непрерывность функции"
- •Раздел 3 Дифференциальное исчисление функции одной переменной
- •Контрольные вопросы
- •Контрольные задания по теме "Дифференциальное исчисление функции одной переменной"
Контрольные задания по теме "Пределы и непрерывность функции"
Задание 2.1
Найти область определения функции.
1.
![]() 2.
2.
![]()
![]()
3.
![]() 4.
4.
![]()
5.
 6.
6.
![]()
7.
 8.
8.
![]()
9.
 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.

17.
![]() 18.
18.

19.
![]() 20.
20.

21.
 22.
22.

23.
![]() 24.
24.
![]()
25.
![]() 26.
26.

27.
![]() 28.
28.
![]()
29.
![]() 30.
30.

Задание 2.2
Найти пределы.
1.
а)
 б)
б)
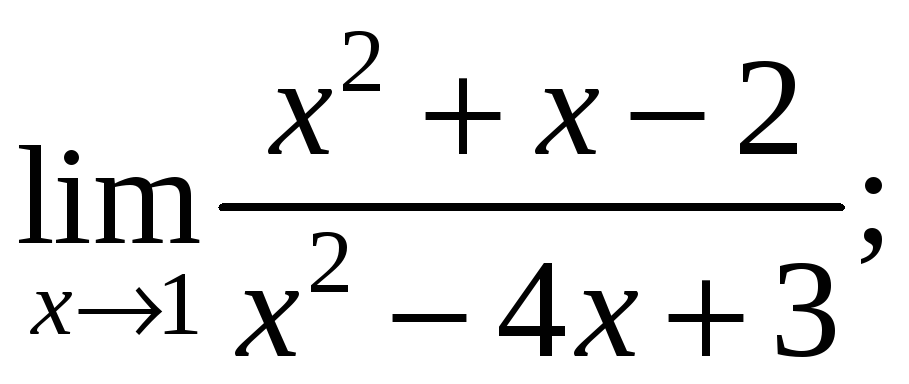 в)
в)

г)

2.
а)
 б)
б)
 ;
в)
;
в)
![]() ;
;
г)

3.
а)
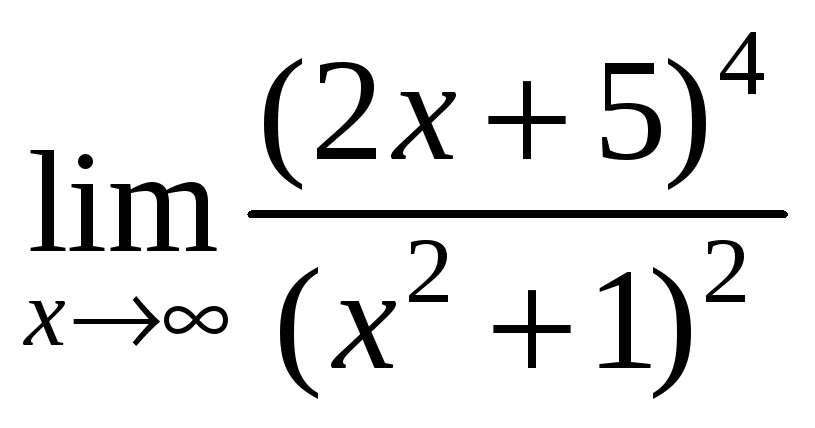 ;
б)
;
б)
 ;
в)
;
в)
![]() ;
г)
;
г)
![]()
4.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

5.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

6.
а)
 ;
б)
;
б)
 ;
в)
;
в)
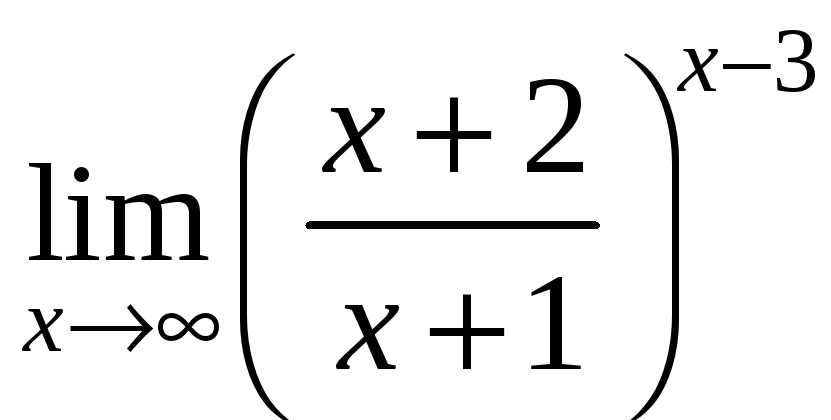 ;
;
г)

7.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
![]()
8.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)

9.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)

10.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)

11.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
![]()
12.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)

13.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)

14.
а) ;
б)
;
б) ;
в)
;
в)![]() ;
;
г)
15.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)![]()
16.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

17.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)

18.
а)
 ;
б)
;
б)
 ;
в)
;
в)
![]() ;
;
г)

19.
а) ;
б)
;
б) ;
в)
;
в)![]() ;
;
г)
![]()
20.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)

21.
а) ;
б)
;
б) ;
в)
;
в) ;
;
г)

22.
а)
 ;
б)
;
б)
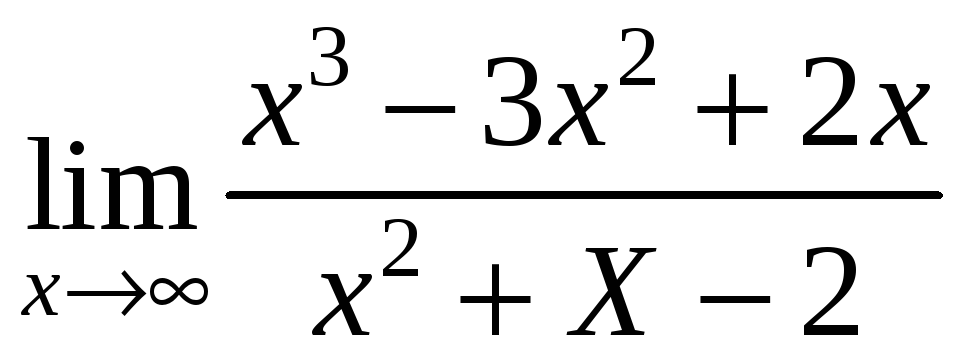 ;
в)
;
в)
 ;
;
г)

23.
а)
 ;
б)
;
б)
 ;
в)
;
в)
![]() ;
;
г)
![]() ;
;
24.
а)
 ;
б)
;
б)
 ;
в)
;
в) ;
;
г)

25.
а)
 ;
б)
;
б)
 ;
в)
;
в)
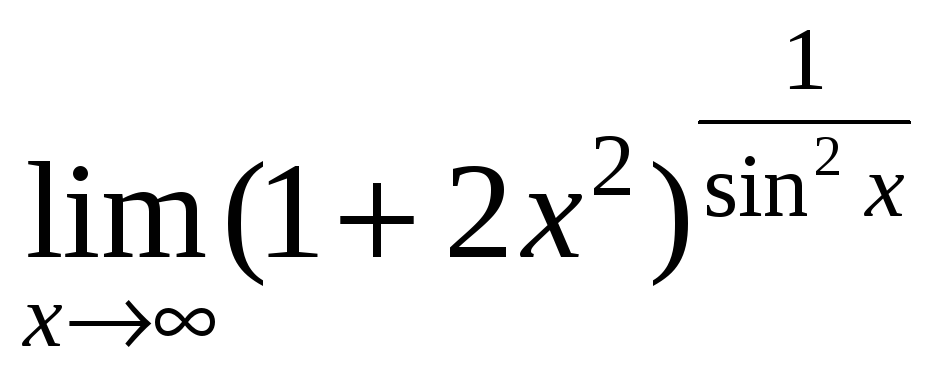 ;
;
г)
![]()
26.
а)
 ;
б)
;
б)
 ;
в)
;
в)
![]() ;
;
г)

27.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
![]()
28.
а)
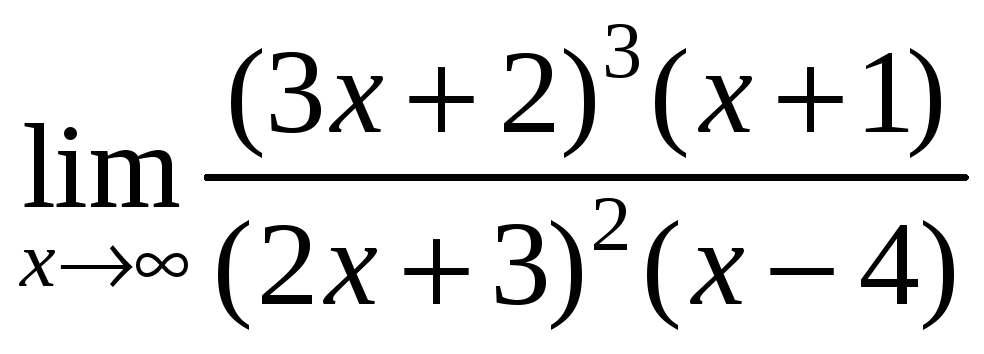 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
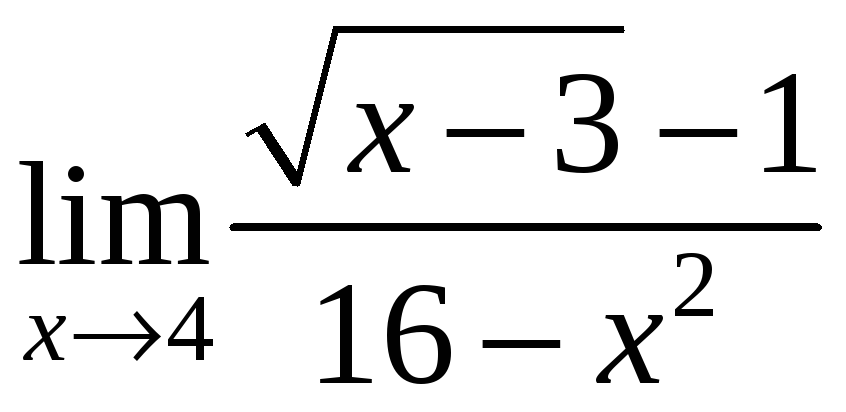
29.
а)
 ;
б)
;
б)
 ;
в)
;
в)
![]() ;
;
г)
![]()
30.
 ;
б)
;
б)
 ;
в)
;
в)
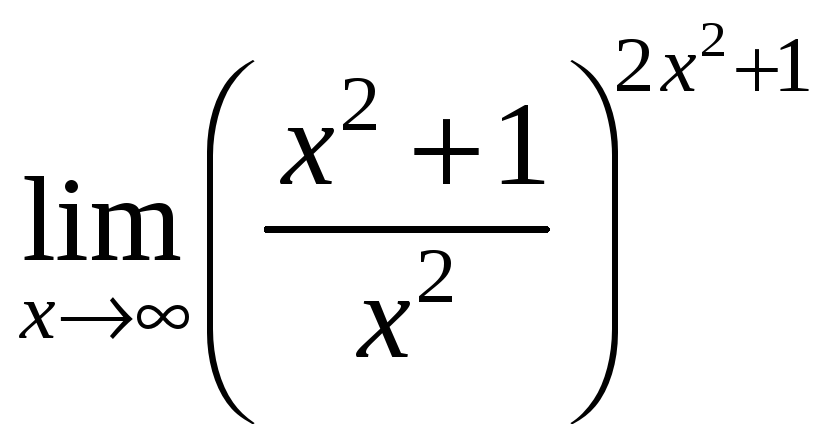 ;
;
г)

Задание 2.3
Исследовать функцию на непрерывность и изобразить схематически ее график в окрестности точек разрыва.
1.
 ;
2.
;
2.
 ;
3.
;
3.
![]() ;
4.
;
4.
![]() ;
5.
;
5.
![]() ;
;
6.
![]() ;
7.
;
7.
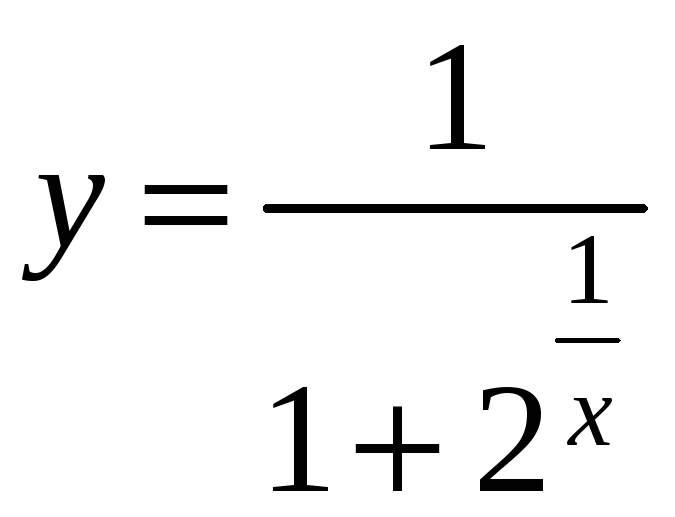 ;
8.
;
8.
![]() ;
9.
;
9.
![]() ;
;
10.
![]() ;
11.
;
11.
![]() ;
12.
;
12.
 ;
13.
;
13.
![]() ;
;
14.
![]() ;
15.
;
15.
 ;
16.
;
16.
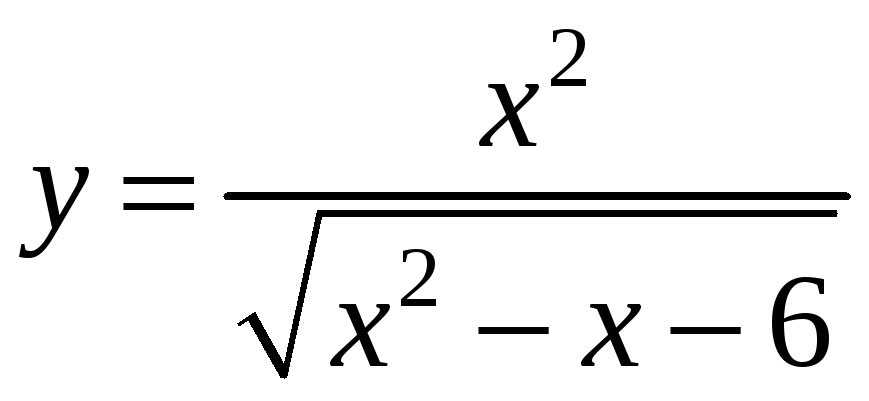 ;
17.
;
17.
![]() ;
;
18.
![]() ;
19.
;
19.
![]() ;
20.
;
20.
 ;
21.
;
21.
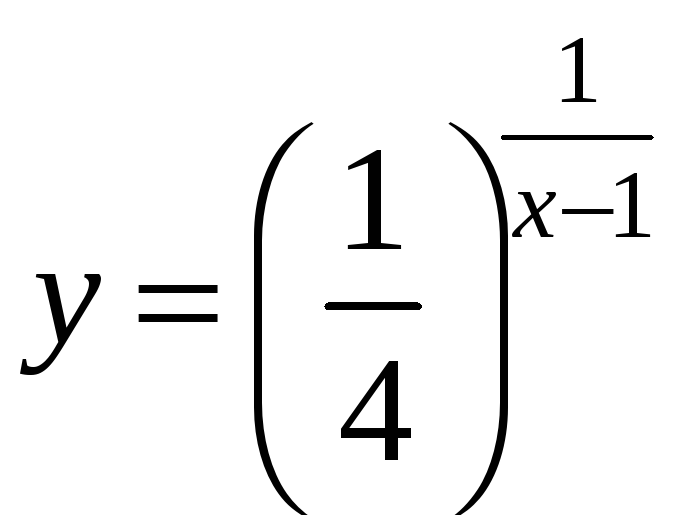 ;
;
22.
![]() ;
23.
;
23.
![]() ;
24.
;
24.
 ;
25.
;
25.
![]() ;
;
26.
 ;
27.
;
27.
![]() ;
28.
;
28.
![]() ;
29.
;
29.
![]() ;
;
30.
 .
.
Задание 2.4
Сравнить бесконечно малые величины.
1.
![]() 2.
2.
![]()
3.
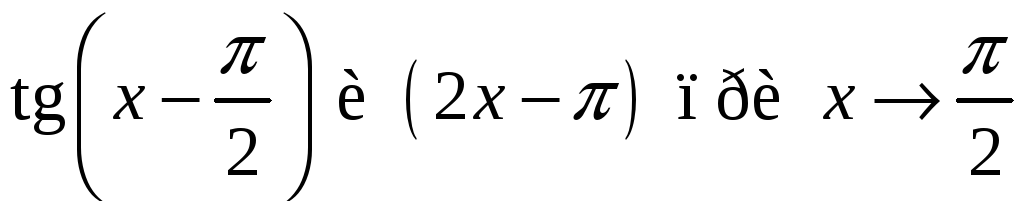 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]()
23.
 24.
24.
![]()
25.
![]() 26.
26.
![]()
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
Раздел 3 Дифференциальное исчисление функции одной переменной
Перед выполнением контрольных заданий по этой теме необходимо изучить теоретический материал по учебникам: [1] (гл.III пар.1, 2, 3(п.47), 4, 5; гл.IV пар. 1, 2, 3); [2] (гл.VI пар. 1-7).
Контрольные вопросы
1. Производная. Геометрический смысл.
2. Дифференцирование суммы, произведения и частного двух функций.
3. Производные основных элементарных функций.
4. Производная сложной и обратной функции.
5. Производная функции, заданной в параметрической форме.
6. Дифференциал, геометрический смысл, свойства.
7. Производные высших порядков.
8. Уравнения касательной и нормали к плоской кривой.
9. Монотонность функции. Необходимый и достаточный признаки монотонности.
10. Экстремум функции. Необходимый и достаточный признаки экстремума функции.
11. Наименьшие и наибольшие значения функции на отрезке.
12. Выпуклость и вогнутость графика функции. Точки перегиба.
Асимптоты.
13. Общий план исследования функции.
Рассмотрим типичные задачи по этой теме.
Задание 3.1
Найти производную заданной функции.
При дифференцировании функции необходимо руководствоваться приведенными ниже правилами.
а) Таблица производных основных элементарных функций:

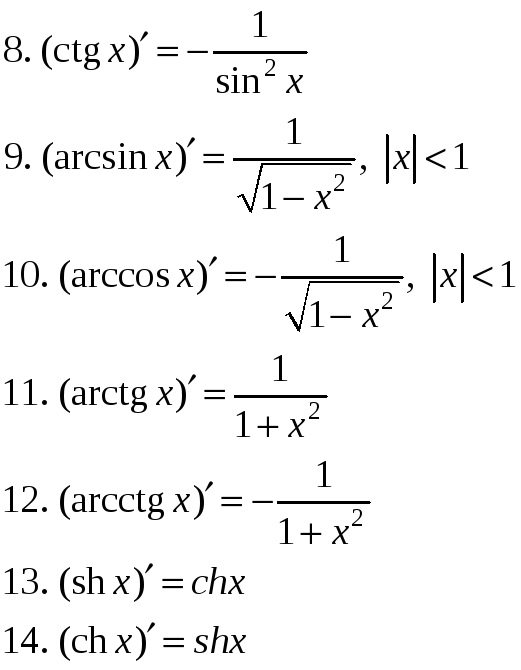
б)
Правила дифференцирования (здесь
![]() – постоянная;
– постоянная;
![]() ,
,
![]() – дифференцируемые функции):
– дифференцируемые функции):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
 ;
;
![]() ;
;
 ;
;
 .
.
Пример 3.1
![]() .
.
![]()





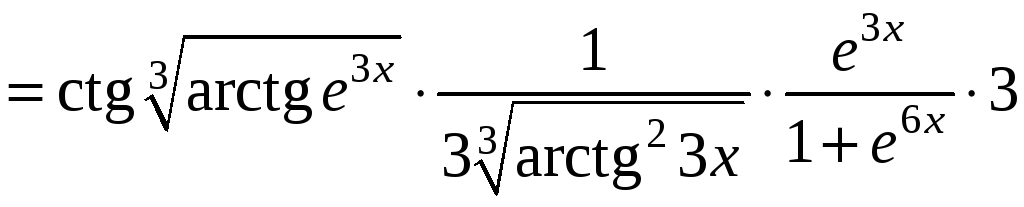 .
.
Пример решен очень подробно для демонстрации правил дифференцирования. Желательно сократить все промежуточные вычисления, тогда решение будет иметь вид:
 .
.
Задание 3.2
Найти
производные
![]() для функции, заданной в параметрической
форме.
для функции, заданной в параметрической
форме.
Пусть
 – параметрически заданная функция.
Тогда
– параметрически заданная функция.
Тогда
 .
.
Обозначим
![]() и рассмотрим следующую параметрически
заданную функцию:
и рассмотрим следующую параметрически
заданную функцию:
 Для вычисления ее производной применяется
правило (*):
Для вычисления ее производной применяется
правило (*):
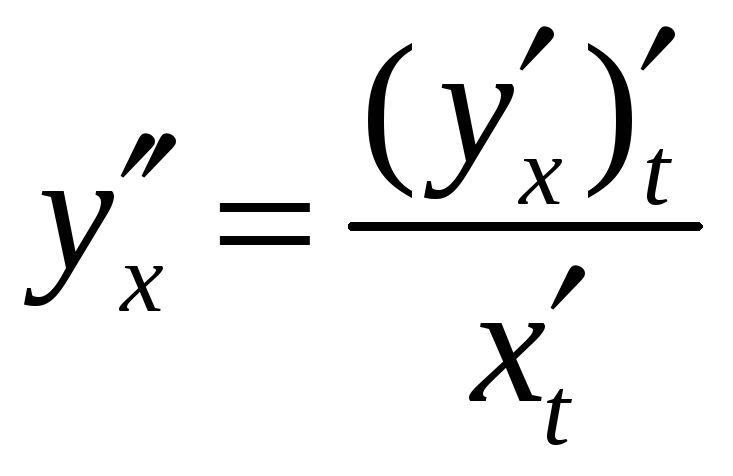 .
.
Повторяя его многократно, можно найти производную любого порядка, если она существует.
Пример 3.2

 .
.
Рассмотрим
функцию
 По формуле (*) находим:
По формуле (*) находим:
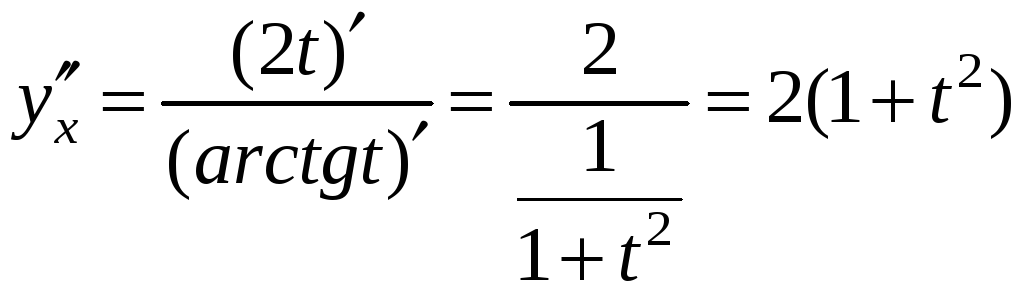 .
.
Задание 3.3
Составить уравнение касательной и нормали к графику функции.
Пусть
![]() – некоторая кривая и
– некоторая кривая и
![]() – точка на ее графике. Тогда
– точка на ее графике. Тогда
 (**)
(**)
–
уравнения касательной и нормали,
соответственно, к графику этой функции
в точке
![]() .
.
Пример 3.3
Составить
уравнения касательной и нормали к кривой
![]() в точке с абсциссой
в точке с абсциссой
![]() .
.
Найдем
![]() ;
;
![]()
![]() – уравнение касательной;
– уравнение касательной;
![]() – уравнение нормали.
– уравнение нормали.
Пример 3.4
 при
при
![]() .
.
Прежде
всего, найдем
![]() ,
при котором
,
при котором
![]() :
:
![]() .
.
Тогда
![]()

![]() – уравнение касательной;
– уравнение касательной;
![]() – уравнение нормали.
– уравнение нормали.
Задание 3.4
Исследовать функцию и построить ее график.
При этом нужно руководствоваться общим планом исследования функции.
1. Найти область определения и точки разрыва функции.
2. Найти точки пересечения графика функции с осями координат.
3. Найти интервалы монотонности и экстремумы.
4. Найти интервалы выпуклости, вогнутости и точки перегиба.
5. Найти асимптоты.
При построении графика функции необходимо учесть ее четность, периодичность, если таковые свойства имеются.
Пример 3.5
Исследовать
функцию
 .
.
1.
Область определения:
![]() .
.
При
![]() функция не определена. Найдем левый и
правый пределы в этой точке:
функция не определена. Найдем левый и
правый пределы в этой точке:
 ;
;
 .
.
Следовательно,
![]() – точка разрыва II – го
рода.
– точка разрыва II – го
рода.
2. Найдем точки пересечения с осями координат.
При
![]()
![]() .
Ось
.
Ось
![]() функция не пересекает, т.к.
функция не пересекает, т.к.
![]() ни при каких
ни при каких
![]() .
.
3. Найдем интервалы монотонности и экстремумы.
 ;
при
;
при
![]() получаем
получаем
 .
.
Отсюда
критические точки:
![]()
Построим таблицу 3.1.
Таблица 3.1
|
|
|
0 |
0,1 |
1 |
1,2 |
2 |
|
|
|
+ |
0 |
– |
не сущ. |
– |
0 |
+ |
|
|
|
max |
|
не сущ. |
|
min |
|
Итак,
точка
![]() – точка максимума,
– точка максимума,
![]() – точка минимума,
– точка минимума,
![]()
4. Найдем интервалы выпуклости, вогнутости и точки перегиба.
 .
.
Критическая
точка
![]() ,
но перегиба в ней нет, так как функция
в этой точке не существует.
,
но перегиба в ней нет, так как функция
в этой точке не существует.
Построим таблицу 3.2.
Таблица 3.2
-

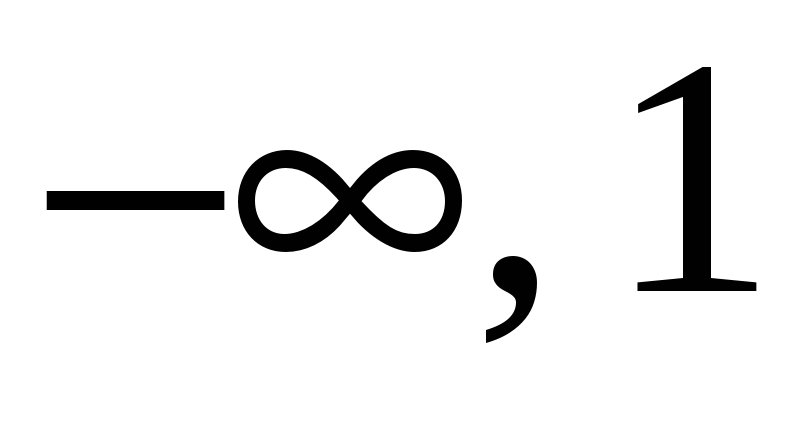
1


–
не сущ.
+


не сущ.

5. Найдем асимптоты функции.
Из
пункта 1 следует, что прямая
![]() – вертикальная асимптота. Рассмотрим
наличие наклонных асимптот:
– вертикальная асимптота. Рассмотрим
наличие наклонных асимптот:
![]() ,
где
,
где
![]()
 ,
,
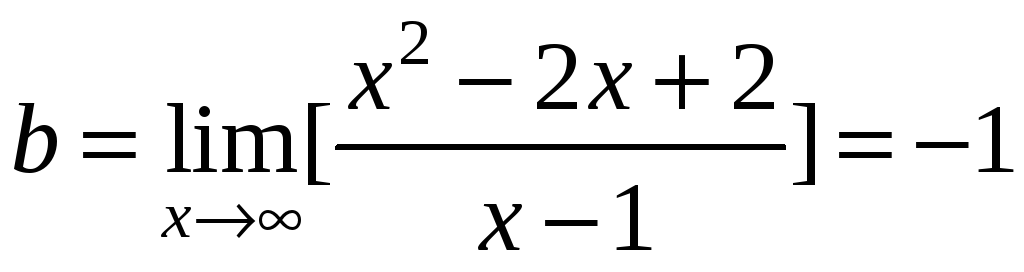 .
.
Наклонная
асимптота существует и ее уравнение
![]() .
.
Исследуемая функция общего характера, не периодическая, нет ни оси, ни центра симметрии.
По полученным результатам строим эскиз графика функции (см. рис. 3.1).

Рис. 3.1
Задание 3.5
Найти наибольшее и наименьшее значения функции на отрезке.
Эти значения непрерывная функция может принять либо в точках экстремума, либо на концах отрезка.
Пример 3.6
![]() .
.
Находим критические точки:
![]()
Вычисляем значения функции в критических точках и на концах отрезка:
![]()
![]() .
.
Сравнивая, их определяем:
![]() ;
;
![]() .
.
