Контрольные задания по теме "Кривые второго порядка"

Задание 1.8

Определить вид линии и построить ее (см. примеры 1.20, 1.21, 1.22):

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

Контрольные задания по теме "Прямая в пространстве и плоскость"

Задание 1.9

Даны три точки . Найти:

1. Уравнение прямой , каноническое и параметрическое (см. пример 1.23, а));

2. Уравнение плоскости (см. пример 123, б));

3. Угол между прямой и плоскостью (см. пример 1.23, в)).

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30. .

Раздел 2 Пределы и непрерывность функции

Перед выполнением контрольных заданий по этой теме необходимо изучить теоретический материал по учебникам [1] (гл.II) или [2] (гл.V).

Контрольные вопросы

1. Множества. Отображение. Функция.

2. Область определения и область значений функции.

3. Предел функции.

4. Предел числовой последовательности.

5. Бесконечно малые величины и бесконечно большие величины. Связь между ними.

6. Свойства бесконечно малых величин.

7. Связь между пределами и бесконечно малыми величинами.

8. Теоремы о пределе арифметических действий.

9. Признаки существования предела.

10. 1-й замечательный предел. Следствия.

11. 2-й замечательный предел. Следствия.

12. Непрерывность функции.

13. Теоремы о непрерывных функциях.

14. Непрерывность сложной функции.

15. Непрерывность обратной функции.

16. Свойства функций, непрерывных на отрезке.

17. Точки разрыва функции.

18. Сравнение бесконечно малых величин и бесконечно больших величин.

Приведем решение типичных задач контрольных заданий с краткими методическими указаниями.

Задание 2.1

При выполнении этого задания удобно пользоваться таблицей областей определения основных элементарных функций.

Таблица 2.1

Функция	Область определения
1. Многочлен: ,
2. Рациональная функция: ,	Определена везде, где
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.

Найти область определения функции.

Пример 2.1

.

Из таблицы 1 следует, что . На числовой оси определяем знаки левой части неравенства (рис. 2.1):

Рис. 2.1

Областью определения является объединение двух множеств:

Пример 2.2

.

Из таблицы 1 следует:

.

Областью определения является пересечение двух множеств: .

Изобразим графически (рис. 2.2):

Рис. 2.2

Задание 2.2

Вычислить пределы.

При нахождении пределов функций необходимо широко использовать следующие понятия:

а) 1-й замечательный предел и его следствия:

б) 2-й замечательный предел и его следствия:

в) понятия эквивалентных (или асимптотически равных) бесконечно малых величин и бесконечно больших величин.

Определение. Если - бесконечно малые или бесконечно большие величины при и то они называются эквивалентными величинам и это обозначается так: .

Предел выражения не изменится, если некоторые величины в нем заменить им эквивалентным. Наиболее часто встречаются следующие эквивалентные бесконечно малые величины при :

; ; ; ; ;

; ; ; ; .

Пример 2.3

.

Пример 2.4

.

Пример 2.5

=.

Пример 2.6

.

Пример 2.7

.

Пример 2.8

.

Пример 2.9

.

Пример 2.10

=.

Пример 2.11

.

Пример 2.12

.

Пример 2.13

.

Задание 2.3

Исследовать функцию на непрерывность.

Функция является непрерывной в точке , если она определена в некоторой окрестности этой точки и . В этом случае существуют лево- и правосторонние пределы:

.

Если в точке существуют левосторонний и правосторонний пределы, но функция не определена в этой точке, то она терпит в точке разрыв I–го рода. При условии равенства этих пределов называется точкой устранимого разрыва.

Если в точке не существует хотя бы один из односторонних пределов, то она называется точкой разрыва II – го рода.

Для исследования функции на непрерывность надо найти левосторонний и правосторонний пределы в точках, где функция не определена.

Пример 2.14

.

;

.

Лево- и правосторонний пределы не существуют, значит – точка разрыва II – го рода (см. рис. 2.3).

Рис. 2.3

Пример 2.15

.

Рассмотрим точку :

;

Левый и правый пределы существуют, и является точкой разрыва I – го рода (см. рис. 2.4).

Рис. 2.4

Пример 2.16

.

Функция не определена в точках

.

Пределы существуют и равны, значит – точка устранимого разрыва (см. рис. 2.5).

Рис. 2.5

;

.

Точка – точка разрыва II – го рода (см. рис. 2.5).

Пример 2.17

.

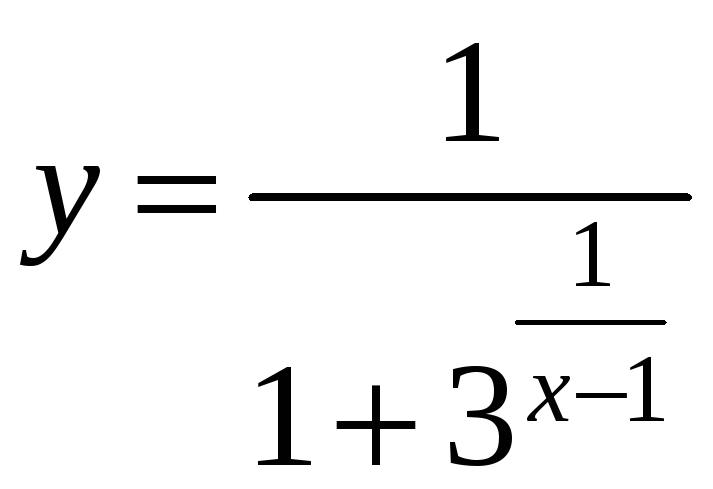Рассмотрим точку :

Пределы существуют, значит – точка разрыва I – го рода (см. рис. 2.6).

Рис. 2.6

Задание 2.4

Для сравнения бесконечно малых величин необходимо найти предел их отношения. Если

1) равен 0, то – бесконечно малая величина более высокого порядка малости, чем ;

2) равен , то – бесконечно малая величина более высокого порядка малости, чем ;

3) равен постоянной , то и - бесконечно малые величины одного порядка малости;

4) равен 1, то – эквивалентные бесконечно малые величины.

Пример 2.18

Сравнить бесконечно малые величины и при .

Составляем предел:

Следовательно, и - бесконечно малые величины одного порядка малости.

Пример 2.19

Сравнить бесконечно малые величины .

. Значит

Пример 2.20

Сравнить бесконечно малые величины при .

. Ответ: .