
- •Раздел 1 элементы линейной алгебры и аналитической геометрии
- •Контрольные вопросы
- •1.1. Элементы линейной алгебры
- •1.2. Действия над векторами
- •1.3. Прямая на плоскости
- •1.4. Кривые второго порядка
- •1.5. Прямая в пространстве и плоскость
- •Контрольные задания по теме "Элементы линейной алгебры"
- •Контрольные задания по теме " Действия над векторами"
- •Контрольные задания по теме "Кривые второго порядка"
- •Контрольные задания по теме "Прямая в пространстве и плоскость"
- •Раздел 2 Пределы и непрерывность функции
- •Контрольные вопросы
- •Контрольные задания по теме "Пределы и непрерывность функции"
- •Раздел 3 Дифференциальное исчисление функции одной переменной
- •Контрольные вопросы
- •Контрольные задания по теме "Дифференциальное исчисление функции одной переменной"
1.5. Прямая в пространстве и плоскость
1)
Общее уравнение плоскости
![]() .
Здесь
.
Здесь
![]() – координаты вектора, перпендикулярного
к данной плоскости:
– координаты вектора, перпендикулярного
к данной плоскости:
![]() .
.
2)
Уравнение плоскости, проходящей через
точку
![]() :
:
![]() .
.
3)
Уравнение плоскости, проходящей через
три точки
![]() ,
,
![]() и
и
![]() :
:
 .
.
4) Каноническое уравнение прямой в пространстве:
 ,
,
где
![]() точка, лежащая на прямой;
точка, лежащая на прямой;
![]() – координаты
направляющего вектора прямой
– координаты
направляющего вектора прямой
![]() .
.
5) Параметрическое уравнение прямой:
![]() ;
;
![]() ;
;
![]() .
.
6)
Уравнение прямой, проходящей через две
точки
![]() и
и
![]() :
:
 .
.
7) Угол между прямой и плоскостью:
 .
.
Пример 1.23
Дано:
![]() .
.
Найти:
а) уравнение прямой, проходящей через
точки
![]() ,
,
![]() ,
в канонической и параметрической форме.
,
в канонической и параметрической форме.
Решение: опираясь на формулы 4, 5, 6, имеем:
![]() – каноническое
уравнение прямой;
– каноническое
уравнение прямой;
параметрическое
уравнение:
![]() ;
;
![]() ;
;
![]() ;
;
б)
уравнение плоскости, проходящей через
точки
![]() .
.
Решение: опираясь на уравнение (3) имеем:
 ;
;  ;
;
![]() .
.
Общее
уравнение плоскости:
![]() .
.
в)
найти угол между прямой
![]() и плоскостью
и плоскостью
![]() .
.
Решение:
![]() ,
, ![]() ;
;
 ;
;
![]() .
.
Ответ:
![]() .
.
Контрольные задания по теме "Элементы линейной алгебры"
Задание 1.1
Даны
матрицы
![]() и
и
![]() .
Найти
.
Найти
![]() (см. пример 1.1).
(см. пример 1.1).
1.
 ;
2.
;
2.
 ;
;
3.
 ;
4.
;
4.
 ;
;
5.
 ;
6.
;
6.
 ;
;
7.
 ;
8.
;
8.
 ;
;
9.
 ;
10.
;
10.
 ;
;
11.
 ;
12.
;
12.
 ;
;
13.
 ;
14.
;
14.
 ;
;
15.
 ;
16.
;
16.
 .
.
Дана
матрица
![]() ;
найти
;
найти
![]() .
.
17.
 ;
18.
;
18.
 ;
19.
;
19.
 ;
;
20.
 ;
21.
;
21.
 ;
22.
;
22.
 ;
;
23.
 ;
24.
;
24.
 ;
25.
;
25.
 ;
;
26.
 ;
27.
;
27.
 ;
28.
;
28.
 ;
;
29.
 ;
30.
;
30.
 .
.
Задание 1.2
Вычислить определитель (см. примеры 1.2, 1.3).
1.
 ; 2.
; 2.
 ; 3.
; 3.
 ; 4.
; 4.
 ;
;
5.
 ; 6.
; 6.
 ; 7.
; 7.
 ; 8.
; 8.
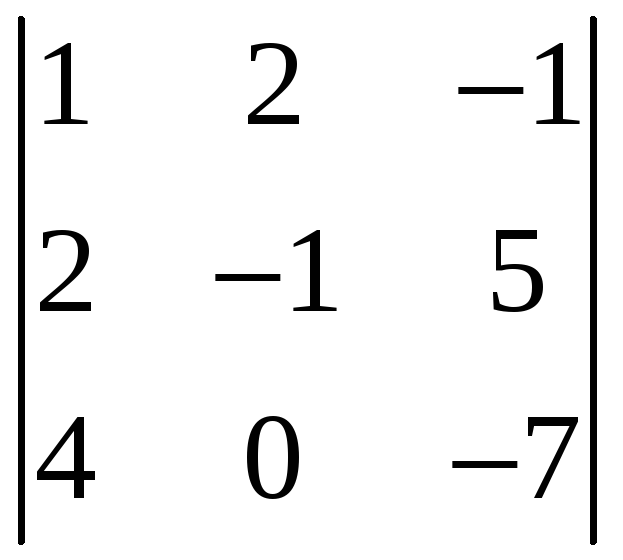 ;
;
9.
 ; 10.
; 10.
 ; 11.
; 11.
 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14.
 ; 15.
; 15.
 ; 16.
; 16.
 ;
;
17.
 ; 18.
; 18.
 ; 19.
; 19.
 ; 20.
; 20.
 ;
;
21.
 ; 22.
; 22.
 ; 23.
; 23.
 ; 24.
; 24.
 ;
;
25.
 ; 26.
; 26.
 ; 27.
; 27.
 ; 28.
; 28.
 ;
;
29.
 ; 30.
; 30.
 .
.
Задание 1.3
Найти матрицу, обратную данной (см. пример 1.4).
1.
 ; 2.
; 2.
 ; 3.
; 3.
 ; 4.
; 4.
 ;
;
5.
 ; 6.
; 6.
 ; 7.
; 7.
 ; 8.
; 8.
 ;
;
9.
 ; 10.
; 10.
 ; 11.
; 11.
 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14.
 ; 15.
; 15.
 ; 16.
; 16.
 ;
;
17.
 ;
18.
;
18.
 ;
19.
;
19.
 ;
20.
;
20.
 ;
;
21.
 ;
22.
;
22.
 ;
23.
;
23.
 ;
24.
;
24.
 ;
;
25.
 ; 26.
; 26.
 ;
27.
;
27.
 ;
28.
;
28.
 ;
;
29.
 ; 30.
; 30.
 .
.
Задание 1.4
Решить систему по формулам Крамера и с помощью обратной матрицы (см. пример 1.5).
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

11.
 12.
12.

13.
 14.
14.

15.
 16.
16.

17.
 18.
18.

19.
 20.
20.

21.
 22.
22.

23.
 24.
24.

25.
 26.
26.

27.
 28.
28.

29.
 30.
30.

Задание 1.5
Исследовать систему на совместность и решить ее методом Гаусса (см. примеры 1.6, 1.7).
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
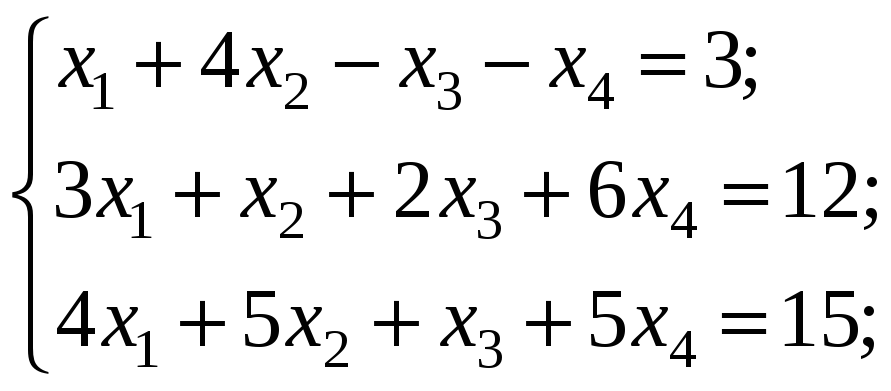 8.
8.

9.
 10.
10.

11.
 12.
12.

13.
 14.
14.

15.
 16.
16.

17.
 18.
18.

19.
 20.
20.

21.
 22.
22.

23.
 24.
24.

25.
 26.
26.

27.
 28.
28.

29.
 30.
30.

Контрольные задания по теме " Действия над векторами"
Задание 1.6
1. Найти косинус угла между
![]() и
и
![]() (см. пример 1.13).
(см. пример 1.13).
2. Найти проекцию
![]() на
на
![]() .
.
3. Вычислить площадь параллелограмма,
построенного на
![]() и
и
![]() (см. пример 1.14).
(см. пример 1.14).
4. Вычислить объём пирамиды с вершинами
в точках
![]() (см. пример 1.15), если:
(см. пример 1.15), если:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]() ;
;
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]() .
.
Задание 1.7
Составить:
1. Уравнение прямой
![]() (см. пример 1.16);
(см. пример 1.16);
2. Уравнение прямой через точку
![]() перпендикулярно прямой
перпендикулярно прямой
![]() (см. пример 1.18);
(см. пример 1.18);
3.
Уравнение прямой через точку
![]() параллельно прямой
параллельно прямой
![]() (см. пример 1.17);
(см. пример 1.17);
4.
Угол
![]() (см. пример 1.19), если:
(см. пример 1.19), если:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]()
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]() .
.
