§ 4.2. Вычисление коэффициента корреляции по выборке

Н ачнем с визуального определения корреляционной зависимости. Для этого строят диаграмму рассеяния на координатной плоскости ХОY (рис.4.2), путем нанесения на координатную сетку (X; Y) множества точек , возможных значений случайных величин Х, Y.

а) r = 0 б) r = 0 в) r > 0

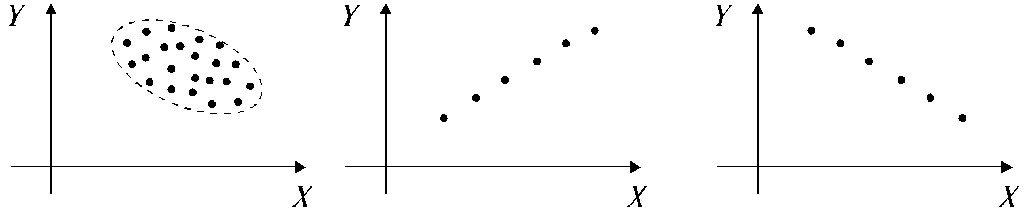
г) r < 0 д) r = 1 е) r = –1.

Рис. 4.2. Визуальное определение корреляционной зависимости

По диаграмме рассеяния.

Изучая рис. 4.2., т.е. множество точек с отчетливо выраженной тенденцией, можно сделать выводы:

1. Рис. 4.2.а) соответствует отсутствию корреляционной зависимости. Переменные Х и Y некоррелированы.

2. Рис. 4.2.б) показывает зависимость Y от Х, которая может быть описана параболой, а не прямой линией. С увеличением Х среднее значение Y остается постоянным, следовательно, коэффициент корреляции равен нулю.

3. На рис. 4.2. в) с возрастанием одной величины среднее значение другой тоже возрастает (корреляция положительная), а на рис. 4.2. г) с возрастанием одной величины другая величина в среднем убывает (корреляция отрицательная).

4. Рис.4.2. д) и е) отражают функциональную зависимость между Y и Х , которую можно записать в виде , где для рис. 4.2. д) и для рис. 4.2. е).

Если объем выборки небольшой, то выборочный коэффициент корреляции вычисляется по формуле

,

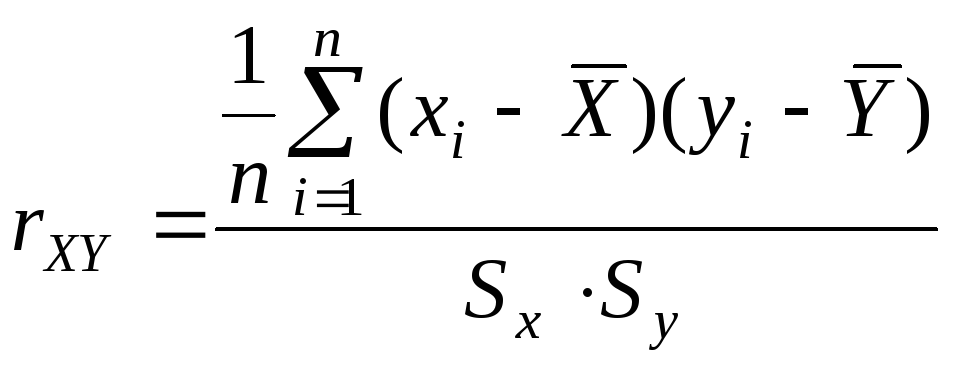где – средние значения,

– средние квадратические отклонения соответственно Х и У.

Если раскрыть скобки и вычислить сумму, то получим

,

где – средняя величина произведения , вычисленная по выборке (это смешанный выборочный начальный момент).

Если n велико (n > 30), то часто переходят к двумерной частотной таблице, которая называется корреляционной. В ней результаты наблюдений записаны в порядке возрастания с указанием частот пар , которые обозначаются через n_ij. Для дискретных случайных величин указано одно значение, для непрерывных – промежуток. Для последующих вычислений, например, вычисления средних и средних квадратических отклонений, берутся середины промежутков.

Из табл. 4.1 видно, что каждому значению Х соответствует не одно значение Y, а распределение Y (строка таблицы). Аналогично, каждому значению Y соответствует распределение Х (столбец таблицы).

Таблица 4.1

Корреляционная таблица

Y X	[y1 – y2) y1	[y2 – y3) y2	. . .	[yl – yl+1) yl
[x1 – x2) x1	n11	n12	. . .	n1l	n1.
[x2 – x3) x2	n21	n22	. . .	n2l	n2.
. . .	. . .	. . .	. . .	. . .	. . .
. . .	. . .	. . .	. . .	. . .	. . .
[xm – xm+1) xm	nm1	nm2	. . .	nml	nm.
	n.1	n.2	. . .	n.l

Вычислим для каждого условного распределения Y среднее значение. Очевидно, что оно зависит от Х. Назовем его условным средним и обозначим через . В зависимости от фиксированного значения получим таблицу.

, где .

Х	x1	x2	. . .	xm
			. . .

Аналогично можно вычислить условные средние для фиксированного значения :

, где .

Y	y1	y2	. . .	yl
			. . .

Если с изменением Х изменяются , то между Х и Y существует корреляционная зависимость. Аналогично определяется зависимость между Y и .

По корреляционной таблице можно также визуально определить существование корреляционной зависимости. Так, если не равны нулю частоты, близкие к центру таблицы, то существует корреляционная зависимость. Если таблица заполнена полностью, то корреляционная зависимость или слабая, или отсутствует.

Оценка парного коэффициента корреляции по корреляционной таблице вычисляется по формуле

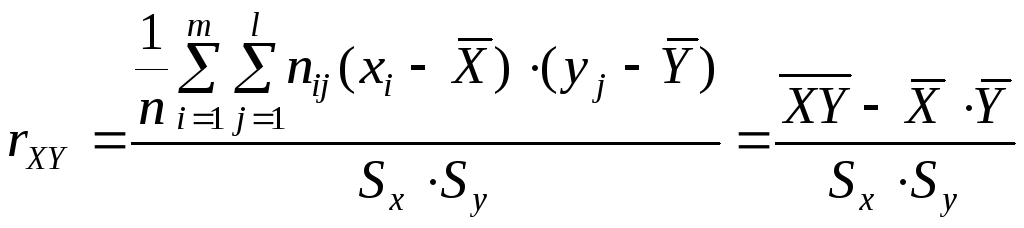, где

В качестве берутся середины соответствующих интервалов.