
- •Авторы: Новротская Надежда Леонидовна, доцент
- •Рецензент: Хацкевич г.А., профессор
- •Часть I
- • Новротская н.Л.
- •Часть I
- •Тема 1. Введение.
- •§1.1. Предмет теории вероятностей.
- •§1.2. Общие правила комбинаторики.
- •§1.3. Вопросы для самопроверки.
- •§1.4. Задачи.
- •Тема 2. Случайные события и их вероятности.
- •§2.1. Случайные события и их классификация.
- •§2.2. Действия с событиями.
- •§2.3. Вероятностное пространство. Вероятности и правила действия с ними.
- •2.3.1. Определение вероятности события.
- •2.3.2. Вероятность суммы событий.
- •Условная вероятность и теорема умножения вероятностей.
- •2.3.5 Формула Байeса (английский математик 1702–1762 г.Г.)
- •§2.4. Модель независимых испытаний Бернулли.
- •2.4.1. Повторные независимые испытания. Формула Бернулли.
- •§2.5. Вопросы для самопроверки.
- •§2.6. Задачи.
- •Тема 3. Случайные величины и их распределения.
- •§3.1. Виды случайных величин и их распределения.
- •§ 3.2. Плотность распределения вероятностей.
- •§ 3.3. Числовые характеристики распределения вероятностей и их свойства
- •3.3.2. Примеры использования математического ожидания.
- •Дисперсия случайной величины и ее свойства.
- •Моменты.
- •3.3.5. Характеристики формы распределения (асимметрия и эксцесс).
- •Квантили.
- •§ 3.4. Примеры распределений.
- •3.4.2. Распределение Пуассона.
- •3.4.3. Гипергеометрическое распределение.
- •3.4.6. Нормальное распределение.
- •3.4.7. Показательное (экспоненциальное) распределение.
- •§ 3.5. Вопросы для самопроверки.
- •§ 3.6. Задачи.
2.3.5 Формула Байeса (английский математик 1702–1762 г.Г.)
Пусть в результате
испытаний произошло событие А.
Оно могло произойти только совместно
с одним из событий
![]() ,
,![]() ,
...,
,
...,
![]() ,
которые образуют полную систему и
безусловные вероятности этих событий
известны. Требуется найти вероятности
событий
,
которые образуют полную систему и
безусловные вероятности этих событий
известны. Требуется найти вероятности
событий
![]() при условии,
что событие А
произошло.
По формуле условной вероятности
при условии,
что событие А
произошло.
По формуле условной вероятности
![]() ,
i=1,
2, ..., n.
,
i=1,
2, ..., n.
Мы получили формулу
Байеса, которая дает выражение послеопытных
вероятностей (апостериорных) через
доопытные (априорные) вероятности.
![]() ,
,
![]() ,
...,
,
...,
![]() называют гипотезами,
поэтому формулу Байеса иногда называют
формулой
гипотез.
Если доопытные вероятности событий
называют гипотезами,
поэтому формулу Байеса иногда называют
формулой
гипотез.
Если доопытные вероятности событий
![]() ,
,![]() ,
...,
,
...,
![]() неизвестны, то их полагают равными:
P(
неизвестны, то их полагают равными:
P(![]() )=
P(
)=
P(![]() )=
...
=P(
)=
...
=P(![]() ).
Тогда формула упрощается и
).
Тогда формула упрощается и
![]() .
.
Формула Байеса может служить основанием для принятия решений после проведения эксперимента. Но для того, чтобы выбор правдоподобной гипотезы имел достаточно оснований, необходимо, чтобы в результате эксперимента ее апостериорная вероятность была достаточно близка к единице.
Пример 1.(продолжение предыдущего). Определить, чему равна вероятность того, что взятое наугад изделие изготовлено первой машиной, если оно оказалось бракованным?
Решение. Необходимо
вычислить P(![]() /
A)
= 0,10,01
/ 0,046 = 0,022.
/
A)
= 0,10,01
/ 0,046 = 0,022.
Пример 2. На складе имеются приборы, изготовленные тремя заводами. 20% изготовлено 1-ым заводом, 50% 2-ым и 30% 3-м заводом. Вероятности, что в течение гарантийного срока прибору потребуется ремонт, для продукции каждого из заводов соответственно равны: 0,2; 0,1; 0,3 . Взятый со склада прибор не имеет заводской маркировки и потребовал ремонта в течение гарантийного срока. Каким заводом вероятнее всего был изготовлен этот прибор? Какова его вероятность?
Решение. Обозначим
через
![]() ={прибор
изготовлен i-ым
заводом},
i=1,2,3,
а через А =
{прибор
дефектный}.
Тогда P(
={прибор
изготовлен i-ым
заводом},
i=1,2,3,
а через А =
{прибор
дефектный}.
Тогда P(![]() )
=
0,2;
P(
)
=
0,2;
P(![]() )
=
0,5;
P(
)
=
0,5;
P(![]() )
=
0,3;
P(A/
)
=
0,3;
P(A/![]() )
= 0,2; P(A/
)
= 0,2; P(A/![]() )
= 0,1;
P(A/
)
= 0,1;
P(A/![]() )
= 0,3; P(A)
= 0,20,2
+ 0,50,1+0,30,3=0,18;
P(
)
= 0,3; P(A)
= 0,20,2
+ 0,50,1+0,30,3=0,18;
P(![]() /
A) = 0,222; P(
/
A) = 0,222; P(![]() /
A) = 0,278; P(
/
A) = 0,278; P(![]() /
A) = 0,5.
Следовательно, вероятнее всего дефектный
прибор изготовлен 3-им заводом.
/
A) = 0,5.
Следовательно, вероятнее всего дефектный
прибор изготовлен 3-им заводом.
§2.4. Модель независимых испытаний Бернулли.
2.4.1. Повторные независимые испытания. Формула Бернулли.
Пусть испытания выполняются по следующей схеме, которая называется схемой Бернулли и удовлетворяет следующим условиям:
1. Испытания независимы, т.е. вероятность события А не зависит от того, появилось или не появилось это событие в других испытаниях.
2. Вероятность
появления события А (успех) одна и та же
в каждом испытании, т.е.![]() ,
а
,
а
![]() .
.
3. Испытания могут повторятся n раз при одних и тех же условиях.
Испытаниями Бернулли будут, например, бросание монеты (герб-успех), контроль на стандартность изделия (стандартное изделие-успех), наблюдение за погодой, проводимые в данный день (скажем, 10 февраля) (дождь-успех) и т.д.. Определению испытаний Бернулли не будут удовлетворять бросания по разному искривленных монет (от бросания к бросанию меняется вероятность успеха), наблюдения за погодой в последовательные дни одного года (нет независимости) и т.д..
Рассмотрим следующую задачу.
В условиях схемы
Бернулли определить вероятность
![]() события A,
состоящего
в том,
что при n
повторных
независимых испытаниях событие A
произойдет
ровно k
раз
безразлично в какой
последовательности.
события A,
состоящего
в том,
что при n
повторных
независимых испытаниях событие A
произойдет
ровно k
раз
безразлично в какой
последовательности.
Пусть
![]() ,
т.е. выполнено одно испытание. Тогда
событие A
наступит с
вероятностью
,
т.е. выполнено одно испытание. Тогда
событие A
наступит с
вероятностью
![]() или наступит противоположное ему событие
или наступит противоположное ему событие
![]() с
вероятностью
с
вероятностью
![]() .
.
Очевидно, что
![]()
При
![]() произойдет одно из следующих событий:
произойдет одно из следующих событий:
![]()
![]()
![]() ,
,
![]() .
.
Эти четыре события попарно несовместны и одно из них обязательно должно произойти, т.е. они образуют полную систему событий. Вычислим вероятности этих событий. События, входящие в произведения, независимы. Поэтому
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
Продолжая вычисления для n=3, 4, 5, ..., k, ... убедимся в том, что, если событие А появилось ровно k раз и не появилось n – k раз, то
![]() .
.
Число таких
комбинаций, если взять другую
последовательность появления события
А, равно
![]() .
Следовательно,
.
Следовательно,
![]() ,
k=0, 1, 2,
..., n.
,
k=0, 1, 2,
..., n.
Эта формула называется формулой Бернулли.
Если вычислить
![]() для всех значений k
и сложить
их, то эта сумма будет равна единице,
как сумма вероятности событий, образующих
полную систему:
для всех значений k
и сложить
их, то эта сумма будет равна единице,
как сумма вероятности событий, образующих
полную систему:
![]()
Из этого равенства получим формулу вероятности появления события A хотя бы один раз в n независимых испытаниях
![]() .
.
Этой формулой
можно воспользоваться для вычисления
числа опытов n,
которые необходимы для того, чтобы с
вероятностью
![]() можно было
утверждать, что событие A
произойдет
по крайней мере один раз.
можно было
утверждать, что событие A
произойдет
по крайней мере один раз.
![]()
![]() Отсюда
Отсюда
![]()
Пример. В лотерее 1000 билетов, среди которых 10 выигрышей по 1млн. рублей, 30 выигрышей по 500 000 рублей, 60 выигрышей по 200 000 рублей и 150 по 60 000 рублей. Найти вероятность кого-нибудь выигрыша при покупке четырех лотерейных билетов.
Решение. Пусть
событие A={выигрывает
лотерейный билет};
событие
![]() {проигрыш}.
{проигрыш}.
Событие А наступит, если произойдет одно из несовместных событий:
![]() {выиграть
1 млн. руб.},
{выиграть
1 млн. руб.},
![]() {
выиграть 500 000 руб.},
{
выиграть 500 000 руб.},
![]() ={
выиграть
200000 руб.},
={
выиграть
200000 руб.},
![]() ={
выиграть
60 000 руб.},
т.е.
={
выиграть
60 000 руб.},
т.е.
![]() По теореме сложения вероятностей найдем:
По теореме сложения вероятностей найдем:
![]() .
.
Тогда
![]()
Отсюда вероятность
хотя бы одного выигрыша при покупке
четырех лотерейных билетов равна
![]()
-
Наивероятнейшее число появления события при повторении испытаний.
Рассмотрим пример. Садовод сделал осенью 6 прививок. По опыту прошлых лет известно, что после зимовки 7 из каждых 10 черенков оставались жизнеспособными. Какое число прижившихся черенков наиболее вероятно?
Решение. Предположим,
что вероятность события A
=
{привитый
черенок приживается}
одинакова для всех черенков и равна 0,7
и что испытания независимы. Составим
таблицу значения вероятностей
![]() для k=0,1,...,6,
учитывая, что p
=
0,7, q
= 0,3, n
=
6.
для k=0,1,...,6,
учитывая, что p
=
0,7, q
= 0,3, n
=
6.
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0,0007 |
0,0102 |
0,0593 |
0,1852 |
0,3241 |
0,3025 |
0,1176 |
Из таблицы видно, что наибольшая вероятность соответствует событию
B ={приживутся 4 черенка}. Следовательно, это событие более возможно, чем другие.
Решим эту задачу в общем виде.
Обозначим число
появлений события A,
имеющего
наибольшую вероятность, через
![]() .
Тогда
.
Тогда
![]() и
и ![]() .
.
Для первого
неравенства имеем 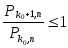
или, учитывая формулу Бернулли,
![]() .
.
После преобразования получим
![]() или
или
![]() .
.
Выполнив те же
преобразования для второго неравенства,
получим
![]() .
Объединив оба неравенства, получим
.
Объединив оба неравенства, получим
![]() .
.
Числа
![]() и
и
![]() отличаются на единицу. Поэтому, если
отличаются на единицу. Поэтому, если
![]() –дробное число, то и
–дробное число, то и
![]() также дробное и неравенство определяет
одно
также дробное и неравенство определяет
одно
![]() .
Если
.
Если
![]() –целое, то и
–целое, то и
![]() –также целое. Тогда
–также целое. Тогда
![]() и
и
![]() будут иметь равную и наибольшую
вероятность.
будут иметь равную и наибольшую
вероятность.
В задаче о садоводе
вычислим
![]() .
Имеем
.
Имеем
![]()
![]()
![]() .
Число
.
Число
![]() -целое,
поэтому
-целое,
поэтому
![]() .
.
Пример. При установившемся технологическом процессе 80% всей произведенной продукции оказывается продукцией высшего сорта. Найти наивероятнейшее число изделий высшего сорта в партии из 250 изделий.
Решение.
![]()
![]()
![]() Тогда
Тогда
![]() следовательно,
следовательно,
![]()
Вычислим вероятность
того, что в партии из 250 изделий окажется
![]() изделий высшего сорта, т.е.
изделий высшего сорта, т.е.
![]()
Непосредственное вычисление вероятности является нелегкой задачей. Поэтому английским математиком Муавром (1667–1754 гг.) была предложена в 1733 г. приближенная формула для частного случая, которая затем была обобщена французским математиком, физиком и астроном Лапласом П.С. в 1812 г. и получила гордое название «центральной предельной теоремы» (см. Тема 5, §2).
2.4.3. Локальная и интегральная теоремы Муавра-Лапласа.
Локальная теорема Муавра-Лапласа.
Теорема.
Если вероятность наступления события
A
в каждом
из n
независимых
испытаний постоянна и ровна p
![]() ,
то справедлива при
,
то справедлива при
![]() следующая приближенная формула
следующая приближенная формула
![]()
где
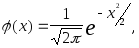 а
а
![]()
Формула дает тем более точный результат, чем больше n.
Для
функции
![]() составлены таблицы. Так как
составлены таблицы. Так как
![]() то таблицы составлены для значений
то таблицы составлены для значений
![]() (см. Приложение).
(см. Приложение).
Продолжим пример.
По условию задачи
![]()
![]()
![]()
![]()
![]() так
как
так
как
![]() и
и
![]() .
.
Окончательно,
![]() .
.
Пример. На опытном поле посеяно 1500 семян. Найти вероятность события A, состоящего в том, что всходы дадут ровно 1200 семян, если считать, что каждое зерно взойдет с вероятностью 0,9.
Решение. Так как n = 1500, k = 1200, p = 0,9, q = 0,1, то
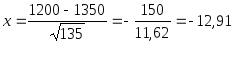 .
.
По таблице
![]() .
.
![]() .
.
Интегральная теорема Муавра-Лапласа.
Теорема. Если
вероятность наступления события A
в каждом
из n
независимых
испытаний постоянна и равна
![]() то справедлива следующая приближенная
формула (при
то справедлива следующая приближенная
формула (при
![]() )
)

где
![]() –
вероятность того, что при n
независимых
повторных испытаниях событие A
наступит
не менее чем
–
вероятность того, что при n
независимых
повторных испытаниях событие A
наступит
не менее чем
![]() раз и не более чем
раз и не более чем
![]() раз,
раз,
![]()
![]()
Интеграл не
выражается через элементарные функции.
Поэтому для вычисления вероятности
пользуются таблицей функции Лапласа
![]() (см.
Приложение)
(см.
Приложение)
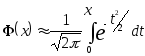 .
.
Свойства
функции
![]() .
.
-
Функция нечетная, т.е.
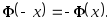 Поэтому в таблице приведены значения
функции для
Поэтому в таблице приведены значения
функции для
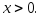 При x=0,
При x=0,

-
Функция
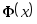 ,
возрастающая на интервале
,
возрастающая на интервале
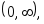 т.к. ее производная положительная при
любом x.
т.к. ее производная положительная при
любом x.
-
При

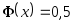 .
.
Замечание.
Имеются таблицы, где
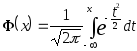 .
.
С помощью функции
Лапласа вероятность
![]() можно вычислить по формуле
можно вычислить по формуле
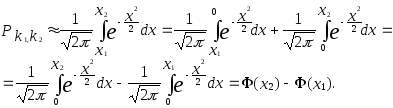
Пример. Вероятность того, что изделие прошло, контроль равна p=0,2. Найти вероятность того, что среди 400 случайно отобранных изделий окажутся прошедшими контроль от 70 до 100 изделий.
Решение. По условию
задачи n
=
400;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
