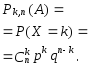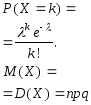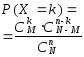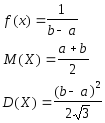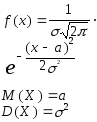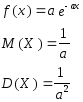- •Авторы: Новротская Надежда Леонидовна, доцент
- •Рецензент: Хацкевич г.А., профессор
- •Часть I
- • Новротская н.Л.
- •Часть I
- •Тема 1. Введение.
- •§1.1. Предмет теории вероятностей.
- •§1.2. Общие правила комбинаторики.
- •§1.3. Вопросы для самопроверки.
- •§1.4. Задачи.
- •Тема 2. Случайные события и их вероятности.
- •§2.1. Случайные события и их классификация.
- •§2.2. Действия с событиями.
- •§2.3. Вероятностное пространство. Вероятности и правила действия с ними.
- •2.3.1. Определение вероятности события.
- •2.3.2. Вероятность суммы событий.
- •Условная вероятность и теорема умножения вероятностей.
- •2.3.5 Формула Байeса (английский математик 1702–1762 г.Г.)
- •§2.4. Модель независимых испытаний Бернулли.
- •2.4.1. Повторные независимые испытания. Формула Бернулли.
- •§2.5. Вопросы для самопроверки.
- •§2.6. Задачи.
- •Тема 3. Случайные величины и их распределения.
- •§3.1. Виды случайных величин и их распределения.
- •§ 3.2. Плотность распределения вероятностей.
- •§ 3.3. Числовые характеристики распределения вероятностей и их свойства
- •3.3.2. Примеры использования математического ожидания.
- •Дисперсия случайной величины и ее свойства.
- •Моменты.
- •3.3.5. Характеристики формы распределения (асимметрия и эксцесс).
- •Квантили.
- •§ 3.4. Примеры распределений.
- •3.4.2. Распределение Пуассона.
- •3.4.3. Гипергеометрическое распределение.
- •3.4.6. Нормальное распределение.
- •3.4.7. Показательное (экспоненциальное) распределение.
- •§ 3.5. Вопросы для самопроверки.
- •§ 3.6. Задачи.
3.4.7. Показательное (экспоненциальное) распределение.
Вернемся к
рассмотрению простейшего потока событий
с интенсивностью а
(см. распределение Пуассона) и введем
непрерывную случайную величину Т–
промежуток времени между двумя появлениями
события. По смыслу
![]() .
Определим для нее функцию распределения:
.
Определим для нее функцию распределения:
![]()
Вероятность
противоположного события
![]() )
равна вероятности того, что в промежутке
времени (0,t)
не наступит
ни одно событие потока, т.е.
)
равна вероятности того, что в промежутке
времени (0,t)
не наступит
ни одно событие потока, т.е.
![]() .
.
Следовательно, вероятность искомого события
![]() при
при
![]()
Определение.
Положительная случайная величина
![]() имеет показательное распределение с
параметром
имеет показательное распределение с
параметром
![]() ,
если ее функция распределения задается
формулой
,
если ее функция распределения задается
формулой
для
для
![]() ,
,![]() .
.![]()
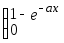
Плотность распределения находится по общему правилу
![]() для
для
![]() .
.
Параметр а в ряде областей именуется «отношением риска».
Числовые
характеристики:
![]()
![]() .
.
Области применения.
Укажем две области.
-
Задачи, связанные с данными типа «времени жизни». В медико-биологических исследованиях под этим термином может подразумеваться продолжительность жизни больных при клинических исследованиях, в технике – продолжительность безотказной работы устройств, в психологии –время, затрачиваемое испытуемыми на выполнение тестовых задач и т.д..
-
Задачи массового обслуживания. Интервалы между вызовами «скорой помощи», телефонными звонками или обращением клиентов и т.д., описываются показательным распределением. Оно широко используется в теории надежности для описания распределения времени безотказной работы прибора или системы, если интенсивность отказа можно считать постоянной; длительности ремонта или другого вида обслуживания.
Пользуясь
показательным распределением можно
определить вероятность того, что время
надежной работы не выйдет из заданного
интервала
![]() .
.
![]() .
.
Задавшись
вероятностью
![]() ,
можно определить время надежной работы,
гарантированной с этой вероятностью,
так как
,
можно определить время надежной работы,
гарантированной с этой вероятностью,
так как
![]() и
и
![]() .
.
Пример 1. Пусть в результате наблюдений за работой системы в течение 100 ч зарегистрировано 5 отказов.
Определить:
1. Функцию надежности системы, т.е. что система будет работать без отказа.
-
Вероятность безотказной работы в течение 50 ч.
-
Время безотказной работы, гарантированное с вероятностью
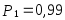 .
.
Решение. Из условия задачи известно, что t = 100, n = 5, a = 5:100 = 0,05 отказа в 1 час.
-
Функция надежности:
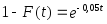 .
. -
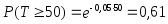 .
. -
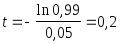 .
.
Пример 2. Среднее время обслуживания покупателя 20 мин. Чему равна вероятность простоя в очереди от 20 до 40 минут?
Решение. Из условия
задачи известно, что
![]() = 20 мин. Следовательно,
= 20 мин. Следовательно,
![]() .
Искомая вероятность
.
Искомая вероятность
![]() .
.
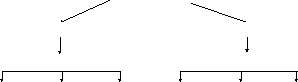
3.4.8. Связь между некоторыми распределениями.
Случайная величина
Дискретная Непрерывная
Распределения Распределения
|
Биноми-альное |
Пуассона |
Гипергео-метрическое |
Равномерное |
Нормальное |
Показательное |
|
|
|
|
|
|
|
Некоторые из
рассмотренных распределений при больших
n
и некоторых
дополнительных условиях сходятся к
другим типам распределений. Например,
биноминальное распределение с параметрами
n
и
p может
быть аппроксимировано нормальным
распределением с
![]() и
и
![]() ,
если выполняются условия npq
>
5 и
,
если выполняются условия npq
>
5 и
![]() .
При условии npq
>
25
эту аппроксимацию можно применять
независимо от значения p.
При условии, что р
<
0,1
и n
велико
биноминальное распределение может быть
аппроксимировано распределением
Пуассона. Распределение Пуассона может
быть аппроксимировано нормальным
распределением с
.
При условии npq
>
25
эту аппроксимацию можно применять
независимо от значения p.
При условии, что р
<
0,1
и n
велико
биноминальное распределение может быть
аппроксимировано распределением
Пуассона. Распределение Пуассона может
быть аппроксимировано нормальным
распределением с
![]() ,
если
,
если
![]() .
Когда
.
Когда
![]() ,
но
,
но
![]() и n
остаются
фиксированными, то гипергеометрическое
распределение сходится к биномиальному.
При малых р,
больших n
и
и n
остаются
фиксированными, то гипергеометрическое
распределение сходится к биномиальному.
При малых р,
больших n
и
![]() гипергеометрическое распределение
может аппроксимироваться распределением
Пуассона.
гипергеометрическое распределение
может аппроксимироваться распределением
Пуассона.