§ 3.5. Обратный обратимый цикл карно

Цикл Карно может протекать не только в прямом, но и в обратном на­правлении (см. рис. 3.4.).

Машины, работающие по обратному циклу, называются холодильными машинами. Это тепловые машины, которые создают и поддерживают раз­ность температур путем отнятия теплоты у более холодного тела и передачи ее более горячему (см. глава 12). А такой процесс, как следует из формули­ровки второго закона термодинамики Клаузиуса, требует затраты энергии (не может совершаться без компенсации).

Рис. 3.4

Рассмотрим обратимый обратный цикл Карно, изображенный на рис. 3.4. В процессе 1-2 рабочее тело (холодильный агент) расширяется по адиабате с уменьшением температуры от T₁ в точке 1 до Т₂ в точке 2. Затем газ расши­ряется по изотерме 2-3 с подводом теплоты q₂ от источника с температурой Т₂. В адиабатном процессе сжатия 3-4 происходит увеличение температуры рабочего тела от Т₂ до T₁. В изотермическом процессе сжатия происходит от­вод от рабочего тела теплоты q₁ к верхнему источнику теплоты.

На осуществление обратного цикла в холодильной машине затрачивается удельная работа l. При этом от НИТ к ВИТ переносится количество теплоты, равное q₂. Кроме того, к ВИТ передается теплота, равная затраченной работе l. Отсюда, вся теплота, получаемая ВИТ, будет q₁=q₂+l. Работа, затрачен­ная на сжатие в процессах 3-4 и 4-1, больше работы расширения в процессах 1-2 и 2-3 на величину площади фигуры 1-2-3-4. Работа расширения произво­дится сжатым газом, и она будет положительной. Работа сжатия производит­ся над газом, и она будет отрицательной. Отсюда суммарная работа, затраченная на передачу теплоты от НИТ к ВИТ, будет отрицательной, и она будет равна l = q₁ - q₂. Эффективность работы холодильных машин характеризу­ется холодильным коэффициентом, определяемым в виде отношения тепло­ты, взятой, от НИТ и переданной ВИТ, к затраченной работе

Холодильный коэффициент характеризует эффективность передачи теп­лоты от НИТ к ВИТ. Он будет тем больше, чем большее количество теплоты q₂ будет взято от НИТ и передано ВИТ и чем меньше будет на это затрачено работы l.

Холодильный коэффициент обратимого обратного цикла Карно определя­ется по формуле

Холодильный коэффициент этого цикла зависит лишь от абсолютных температур T₁ и Т₂ и имеет наибольшее значение по сравнению с холодиль­ными коэффициентами любых других циклов, протекающих в тех же темпе­ратурных пределах.

Холодильные машины, предназначенные для отопления помещений пу­тем передачи теплоты от источника с более низкой температурой к источни­ку с более высокой температурой, называются тепловыми насосами.

Их эф­фективность оценивается отопительным коэффициентом φ, определяемым по формуле (см. § 12.5)

§ 3.6. Метод циклов. Открытие энтропии как функции состояния

В термодинамике большое распространение получил так называемый метод циклов, разработанный Клапейроном на основе идей Карно. До введения Гиббсом в 1870 г. метода потенциалов это был единственный метод, позволявший устанавливать связи между термодинамическими характеристиками процессов, связанных с преобразованиями, в которых участвуют теплота и работа.

Сравнивая формулы для кпд обратимого цикла Карно η_t=(T₁-T₂)/T₁ и η_t=(Q₁-Q₂)/Q₁ (см. формулу (3.3)), получим

По формуле (3.3) может быть найден кпд любого цикла, в том числе и цикла Карно.

Отсюда

(3.8)

Величина Q/T, отнесенная к тому или иному телу, называется приведенной теплотой.

Из формулы (3.8) следует равенство приведенных теплот нагревателя и холодильника в цикле Карно.

Можно показать, что цикл Карно всегда можно разбить на два или больше циклов промежуточными адиабатами (рис. 3.5.) [15]. Такое деление цикла является обоснованным потому, что промежуточные адиабаты проводятся в противоположных направлениях, и оба процесса по такой адиабате взаимно компенсируются. Разобьем цикл Карно на два цикла с помощью адиабаты ab (см. рис. 3.5.). Тогда теплоты Q₁ и Q₂ разделяются на части

Рассмотрев каждый из образованных циклов, получим равенство приведенных теплот согласно (3.8)

Рис. 3.5 Рис. 3.6

Сложив эти равенства, находим

и вообще при разделении на несколько циклов будем иметь

(3.9)

Допустимо также составление циклов Карно, где участвуют нагреватели и холодильники с различными температурами в разных циклах. И в этом случае составление ведется по адиабатам (рис. 3.6.). Обобщая выражение (3.9) на n циклов, получим

(3.10)

Наряду с циклами, где происходит передача конечных количеств тепла Q₁ и Q₂, можно представить элементарные циклы, в которых передаются бесконечно малые количества тепла dQ₁ и dQ₂ при конечной разности температур T₁ и T₂. Для такого цикла

Пользуясь возможностью разбиения циклов на части любой обратимый цикл можно разбить на большое количество узких элементарных циклов Карно, соприкасающихся по адиабатам (рис. 3.7.).

Рис. 3.7

При этом отрезки адиабат, лежащие внутри контура, взаимно компенсируются. Некоторая ошибка получается вследствие замены непрерывного контура ступенчатыми изотермами сверху и снизу, а также нескомпенсированными отрезками адиабат, прилегающих к контуру. Однако при переходе к пределу, когда dQ₁⁽ⁱ⁾ и dQ₂⁽ⁱ⁾ стремятся к нулю, эта ошибка может быть сделана сколь угодно малой. Выражение (3.10) для конечного числа элементарных циклов в пределе будет иметь вид

(3.11)

Выражение (3.11) можно переписать в виде

(3.12)

Выражение (3.12) можно рассматривать как алгебраическую сумму при переменных dQ и Т. Так как эта сумма относится ко всему контуру, то из (3.12) следует

(3.13)

Выражение (3.13) является интегралом Клаузиуса для любого обратимого цикла. Отсюда следует, что интеграл приведенных теплот для любого обратимого цикла для всех веществ равен нулю.

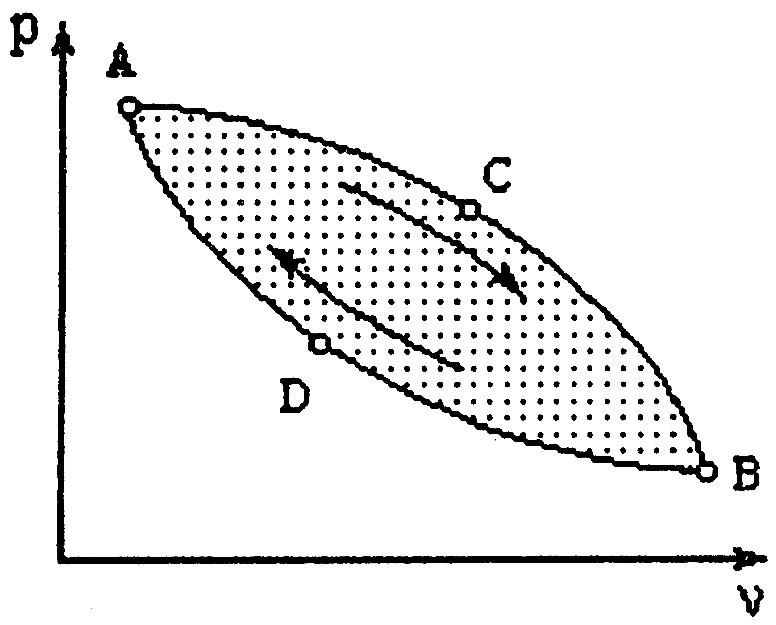
Рис. 3.8

Из соотношения (3.13) следует, что не зависит от формы пути.

Например, при изменении состояния от точки А до точки В (рис. 3.8.) по пути АСВ получим

а при движении от А к В по пути ADB будем иметь

Отсюда, следуя (3.13), можно записать

или

Так как интеграл по замкнутому контуру от равен нулю, а также учитывая, что изменение этой величины не зависит от формы пути, приходим к выводу, что бесконечно малая величина есть полный дифференциал некоторой функции S параметров состояния

(3.14)

Эта функция состояния называется энтропией. Интегрируя (3.14), получим общее выражение для энтропии

(3.14а)

где константа (const) является неопределенной постоянной интегрирования. Отсюда следует новая математическая формулировка второго начала:

величина есть полный дифференциал. Таким образом, установлено существование энтропии как функции состояния. Согласно выражению (3.14) энтропия имеет следующую единицу измерения:

для 1 кг массы s, Дж/(кг·К);

для любого количества вещества S, Дж/К.

Абсолютное значение энтропии может быть найдено лишь в случае, если будет известна неопреде­ленная постоянная интегрирования.