Тема 5. Кластерный анализ

Процесс разбивки объектов на кластеры носит название кластерного анализа. Однородность объектов определяется по расстоянию

где векторы, элементы которых – составляющие. Объекты считаются однородными, если Для объектов, характеризуемых числовыми признаками, расстояние определяют так:

Расстояние между объектами, описываемыми атрибутивными признаками:

Графическое изображение объединения кластеров может быть получено с помощью дерева объединения кластеров – дендрограммы (греч. Dendron ­– дерево). Дендрограмма – графическое изображение древовидных структур.

Типичная дендрограмма приведена на рисунке 4.

Пример. Провести классификацию шести производственных объектов, каждый из которых характеризуется двумя признаками: индекс групповой сплоченности; обобщенный уровень мотивации к совместной деятельности.

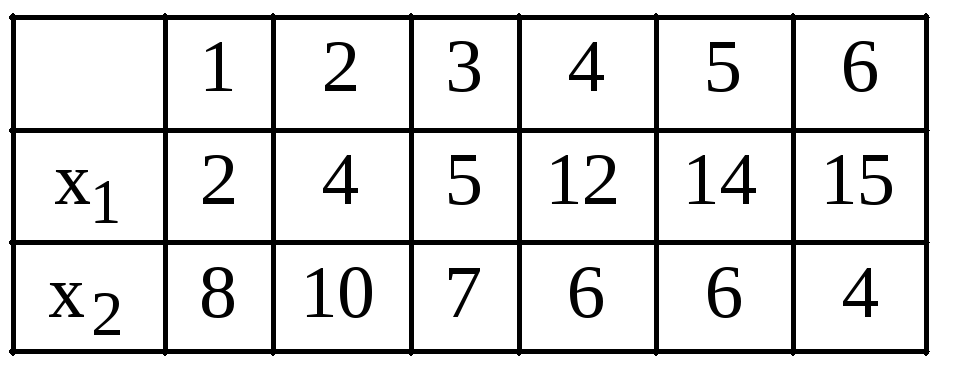
Найдем расстояние между объектами:

Рассчитав все расстояния, заполним таблицу:

1 2 3 4 5 6

1 0 2,83 3,16 10,19 12,17 13,6

2 0 3,16 8,94 10,77 12,53

3 0 7,07 9,06 10,44

4 0 2 3,61

5 0 2.24

6 0

Предлагаем вам самостоятельно проверить значения всех расстояний.

Применим принцип «ближайшего соседа». Найдем наименьшее из расстояний

Таким образом, можно объединить в группу 4 и 5 объекты. В исходной матрице расстояний получим:

1 2 3 4, 5 6

1 0 2,83 3,16 10,19 13,6

2 0 3,16 8,94 12,53

3 0 7,07 10,44

4 0 3,61

5 2,24

6 0

Продолжим:

1 2 3 4, 5, 6

1 0 2,83 3,16 10,19

2 0 3,16 8,94

3 0 7,07

4, 5, 6 0

Продолжим:

1,2 3 4, 5, 6

1, 2 0 3,16 8,94

3 0 0 7,07

4, 5, 6 0

И окончательно

1, 2, 3 4, 5, 6

1, 2, 3 0 7,07

4,5,6 0 0

Таким образом, проведя кластерный анализ по методу «ближайшего соседа», получим 2 кластера. Дендрограмма при этом имеет вид, показанный на рисунке 4.

7,07

3,16

2,83 2,24

2,0

1 2 3 4 5 6

Рисунок 4

Задание 5. Провести классификацию шести социальных групп по принципу «ближайшего соседа», каждый из которых характеризуется двумя признаками.

Построить дендрограмму, где индивидуальные параметры студента: количество букв в фамилии студента; количество букв в полном имени студента; номер студента в списке группы по журналу; индекс групповой сплоченности; обобщенный уровень мотивации к совместной деятельности.