
- •Математические методы в психологии
- •Тема 1. Дискретный вариационный ряд и его основные показатели Выбор варианта задания
- •Методика выполнения задания 1
- •Тема 2. Статистический анализ выборочных средних двух выборок Методика выполнения задания 2
- •Процедура проверки статистических гипотез заключается в следующем.
- •-Критерий Стьюдента
- •Алгоритм расчета t-критерия Стьюдента для независимых выборок измерений
- •Алгоритм расчета -критерия Стьюдента для зависимых выборок измерений
- •-Критерий Манна-Уитни
- •Алгоритм расчета критерия Манна-Уитни
- •Критерий знаков
- •Алгоритм расчета критерия знаков
- •1. Подсчитать количество нулевых реакций и исключить их из рассмотрения. В результате уменьшится на количество нулевых реакций.
- •Задание 2
- •Тема 3. Вычисление и анализ коэффициента ранговой корреляции Методика выполнения задания 3 Выполнить ранжирование по следующему алгоритму
- •Алгоритм расчета коэффициента ранговой корреляции Спирмена
- •Задание 3
- •Тема 4. Многомерное шкалирование
- •Тема 5. Кластерный анализ
- •Тема 6. Уравнение линейной регрессии Методика выполнения задания 6
- •1. Анализ статистической взаимосвязи между двумя рядами
- •2. Построение модели парной регрессии
- •Оформление задания
- •Варианты к заданию 6
- •Математическое моделирование
- •Классификация по целевому назначению
- •Классификация по типу задач
- •Классификация по форме реализации
- •Типы задач линейного программирования
- •Тема 7. Каноническая задача линейного программирования
- •Стандартная задача линейного программирования
- •Общая задача линейного программирования
- •Графический метод решения задач линейного программирования
- •Задание 7
- •Тема 8. Нелинейное программирование. Понятие о задаче математического программирования. Оптимизационная задача на условный экстремум
- •Задание 8
- •Библиографический список
2. Построение модели парной регрессии
Построение
уравнения регрессии
![]() (1) сводится
к оценке (расчету) ее параметров
(коэффициентов)
(1) сводится
к оценке (расчету) ее параметров
(коэффициентов)
![]() и
и
![]() Для оценки параметров уравнения регрессии
используют метод
наименьших квадратов
(МНК). Сущность МНК заключается в
нахождении параметров модели, при
которых минимизируется сумма квадратов
отклонений эмпирических (фактических)
значений отклика от теоретических,
вычисленных по модели. Сказанное можно
записать в следующем виде:
Для оценки параметров уравнения регрессии
используют метод
наименьших квадратов
(МНК). Сущность МНК заключается в
нахождении параметров модели, при
которых минимизируется сумма квадратов
отклонений эмпирических (фактических)
значений отклика от теоретических,
вычисленных по модели. Сказанное можно
записать в следующем виде:
 (7)
(7)
Нахождение
коэффициентов уравнения регрессии по
МНК производится из системы нормальных
уравнений. Данную систему получают
путем приравнивания нулю всех частных
производных функции
![]() . В качестве
аргументов функции
. В качестве
аргументов функции
![]() рассматриваются коэффициенты уравнения
регрессии.
рассматриваются коэффициенты уравнения
регрессии.
Для уравнения (4) формула (7) примет следующий вид :
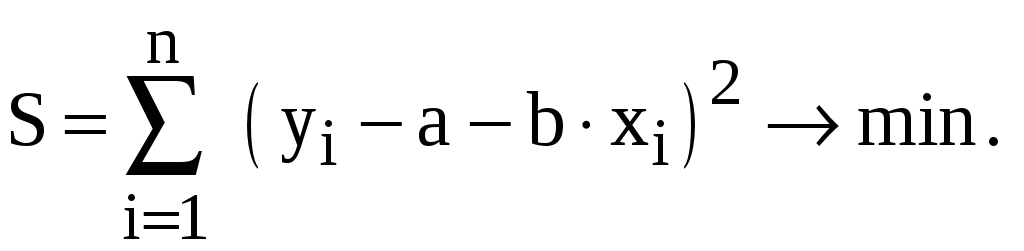 (8)
(8)
Дифференцируя
функцию
![]() из
(5) по
параметрам
из
(5) по
параметрам
![]() и
и
![]() ,
получаем
,
получаем
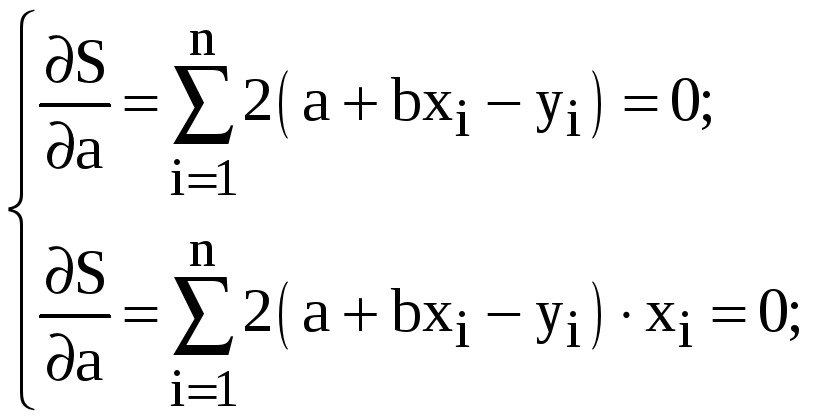
Отсюда система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
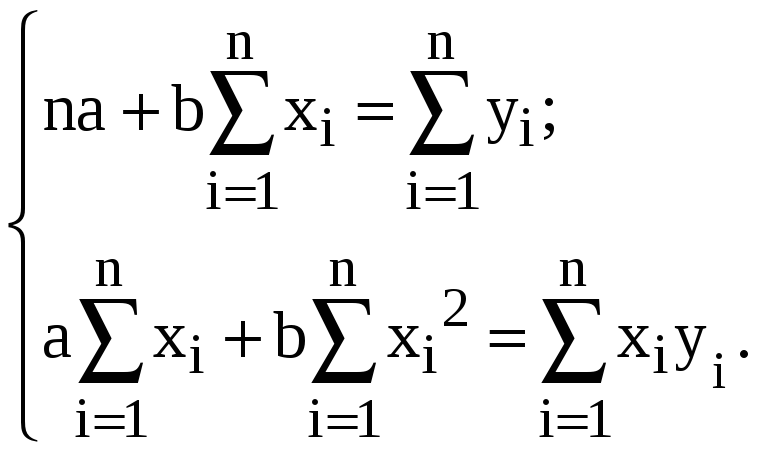 (9)
(9)
Решая систему
(9) относительно
![]() и
и
![]() получаем следующие формулы:
получаем следующие формулы:
![]()

где
![]() соответствующие
средние.
соответствующие
средние.
Анализ качества модели парной регрессии
Под анализом
понимается оценка аппроксимации
(качества) или проверка адекватности
построенной модели. Для оценки
аппроксимации используются такие
характеристики, как средняя ошибка
аппроксимации
![]() и
и
![]() критерий (критерий Фишера)
критерий (критерий Фишера)
![]()
Средняя ошибка
аппроксимации
![]() - среднее
отклонение расчетных значений отклика
от его фактических
– вычисляется
по формуле:
- среднее
отклонение расчетных значений отклика
от его фактических
– вычисляется
по формуле:
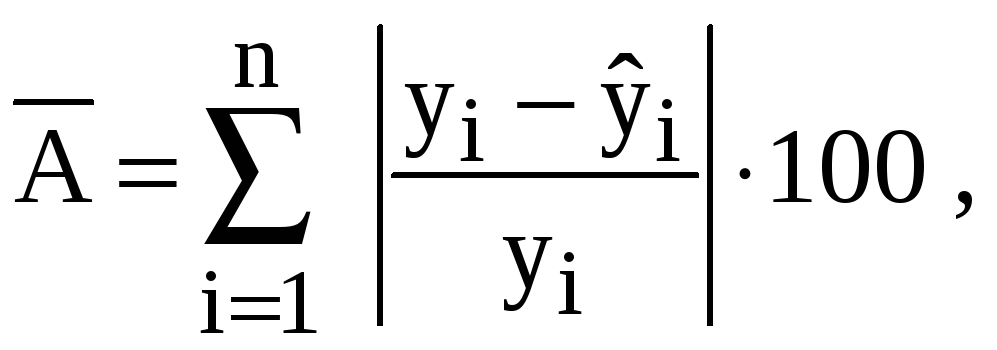
где
![]() – наблюдаемые значения;
– наблюдаемые значения;
![]()
Допустимый
предел значений
![]() - не более
8-10 %.
- не более
8-10 %.
Вычисление
характеристики
![]() осуществляется с использованием
следующих формул:
осуществляется с использованием
следующих формул:
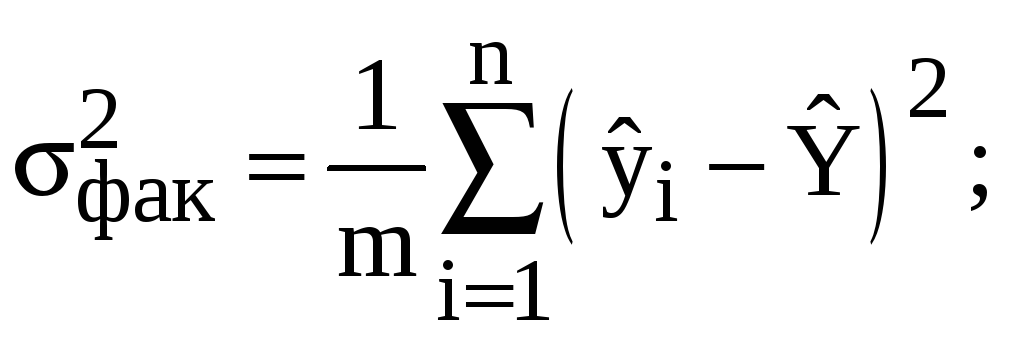 (10)
(10)
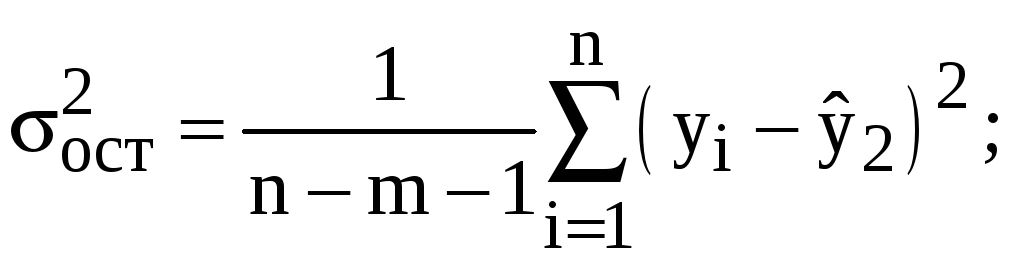 (11)
(11)
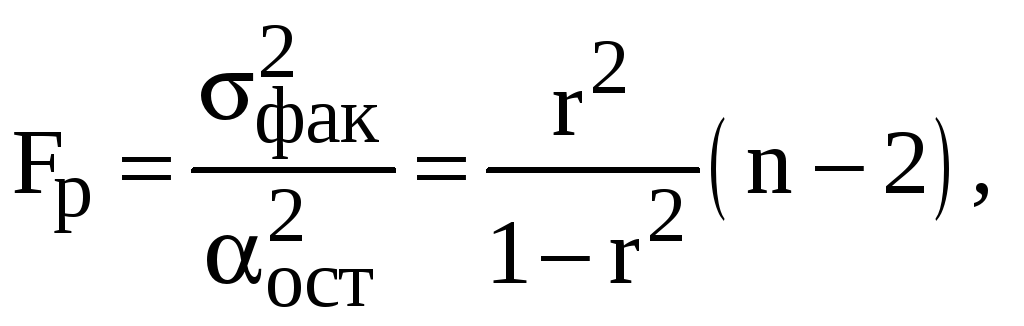 (12)
(12)
где
![]() эмпирические
(наблюдаемые) значения
эмпирические
(наблюдаемые) значения
![]() ;
;
![]() расчетные значения
расчетные значения
![]() ;
;
![]() среднее
значение, вычисленное по ряду
среднее
значение, вычисленное по ряду
![]()
![]() количество
коэффициентов при переменной
количество
коэффициентов при переменной
![]() в уравнении регрессии (для уравнения
вида (1) –
в уравнении регрессии (для уравнения
вида (1) –
![]() ).
).
Оценка
аппроксимации (адекватность модели)
уравнения регрессии осуществляется с
помощью
![]() -критерия
следующим образом. На основе заданных
уровня
-критерия
следующим образом. На основе заданных
уровня
значимости
![]() (обычно,
(обычно,
![]() или
или
![]() ),
чисел степеней свободы
),
чисел степеней свободы
![]() и
и
![]() определяется табличное значение
определяется табличное значение
![]() из специальных таблиц, в частности
(прил., табл. А4). Если
из специальных таблиц, в частности
(прил., табл. А4). Если
![]() то модель считается адекватной. В
противном случае модель неадекватная,
т. е. зависимость между случайными
величинами
то модель считается адекватной. В
противном случае модель неадекватная,
т. е. зависимость между случайными
величинами
![]() и
и
![]() не является линейной.
не является линейной.
