Контрольні запитання.

1. Дати означення лінійного диференціального рівняння другого порядку.

2. В чому полягає різниця між однорідними і неоднорідними диференціальними рівняннями?

3. Як залежить розв’язок лінійного диференціального рівняння другого порядку з сталими коефіцієнтами від розв’язків характеристичного рівняння?

4. В чому полягає задача Коші для рівнянь другого порядку?

Література: [1] -§ 62, 63.

Урок № 29

Тема: Застосування рядів до наближених обчислень.

План:

1. Обчислення значень функцій.

2. Обчислення визначених інтегралів.

3. Розв’язування диференціальних рівнянь.

Елементарні функції можна розкласти в ряд:

Користуючись розкладом у степеневі ряди, можна обчислювати наближені значення визначених інтегралів, границі та інше. У таких обчисленях зберігають п перших членів ряду, а останні відкидають. Для оцінки похибки знайденого наближеного значення потрібно оцінити суму відкинутих членів. На практиці оцінку проводять так: якщо ряд знакосталий, то його залишок порівнюють з геометричним рядом, члени якого утворюють спадну геометричну прогресію, а якщо ряд знакозмінний і його члени задовольняють умовам Лейбніца, то використовують оцінку , де - перший з відкинутих членів ряду.

Приклад . Використовуючи розклад функції в ряд обчислити значення виразу з точністю до 0,001: .

Завдання. Використовуючи розклад функції в ряд обчислити значення виразу з точністю до 0,001: .

Контрольні запитання.

1. Дати означення числового ряду.

2. Дати означення функціонального ряду.

3. Який ряд називається знакозмінним?

4. Дати означення степеневого ряду.

5. Як оцінити на практиці залишок ряду.

Література: [1] -§ 83.

Урок № 34

Тема: Розв’язування систем лінійних рівнянь методом оберненої матриці.

План:

1. Матричне рівняння

2. Розв’язування матричного рівняння.

Нехай дана система лінійних рівнянь з трьома невідомими:

.

Розглянемо матрицю системи і матриці невідомих та вільних членів: 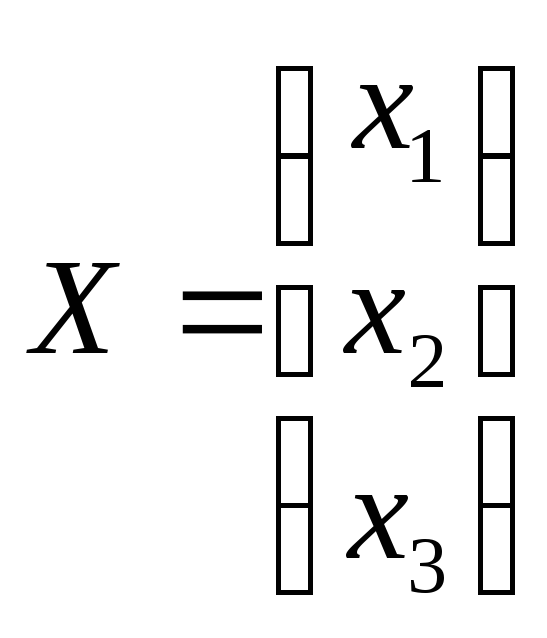та .

Запис називається матричним рівнянням. Можна довести, що . Такий метод розв’язування систем лінійних рівнянь називається матричним.

Приклад . Розв’язати систему лінійних рівнянь матричним методом.

Завдання: Розв’язати систему лінійних рівнянь матричним методом.

Контрольні запитання.

1. Дати означення матриці оберненої до даної.

2. Яка необхідна і достатня умова невиродженості матриці?

3. Як знайти матрицю обернену до даної?

4. Дати означення добутка двох матриць.

5. Що називають матричним рівнянням і як знайти розв’язок цього рівняння?

Література: [12] - § 18-19, [13] - § 1