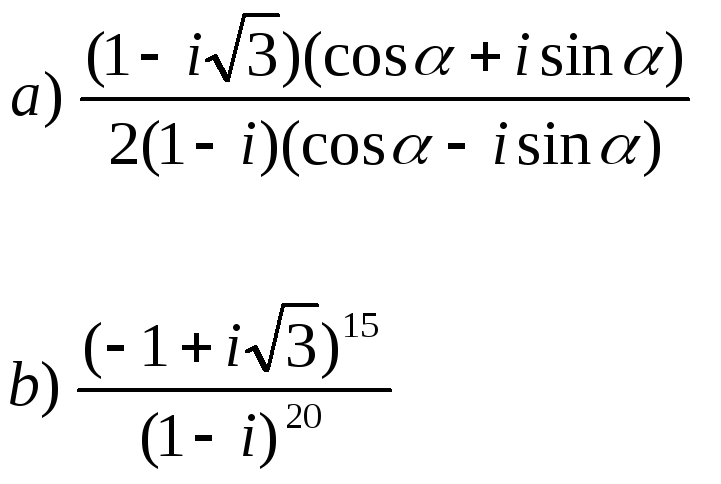46

Міністерство освіти і науки України

Машинобудівний технікум Кіровоградського державного технічного університету

Методичний збірник для допомоги студентам у вивченні самостійних тем по предмету основи вищої математики

Спеціальність 5. 090231 «Обслуговування верстатів з програмним управлінням і робототехнічних комплексів».

Розробив викладач Сєрякова О.В.

(підпис)

Розглянуто на засіданні

предметної (циклової)

комісії фізико- математичних

дисциплін.

Протокол № від

Голова комісії Боліла В.А.

Кіровоград 2003 р.

Урок № 2

Тема: Алгебраїчна форма комплексного числа. Розв’язування вправ.

План

1. Алгебраїчна форма комплексного числа.

2. Розв’язування квадратних рівнянь із дійсними коефіцієнтами.

3. Дії над комплексними числами, представленими в алгебраїчній формі.

Означення: Комплексним числом називається вираз вигляду , де а, b – дійсні числа, і – уявна одиниця (алгебраїчна форма комплексного числа).

а – дійсна частина комплексного числа,

• у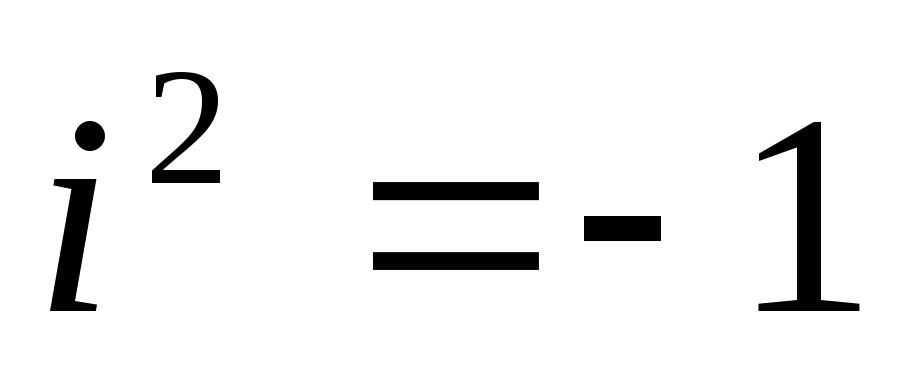явна частина комплексного числа,

Для уявної одиниці виконується рівність .

Множина комплексних чисел позначається С.

Якщо b=0, то z=a+0i=a – дійсне число. Отже, множина дійсних чисел є підмножиною множини комплексних чисел.

Якщо а=0, то - суто уявне число.

Означення: Два комплексних числа називаються спряженими, якщо вони відрізняються лише знаком уявної частини.

Якщо дискриминант квадратного рівняння від’ємне число, то корені цього рівняння – взаємно спряжені комплексні числа: .

Додавання, віднімання та множення комплексних чисел здійснюється за правилами додавання, віднімання та множення двох біномів.

Для того щоб поділити два комплексних числа в алгебраїчній формі необхідно домножити чисельник і знаменник дробу на число спряжене до знаменника і виконати дії.

П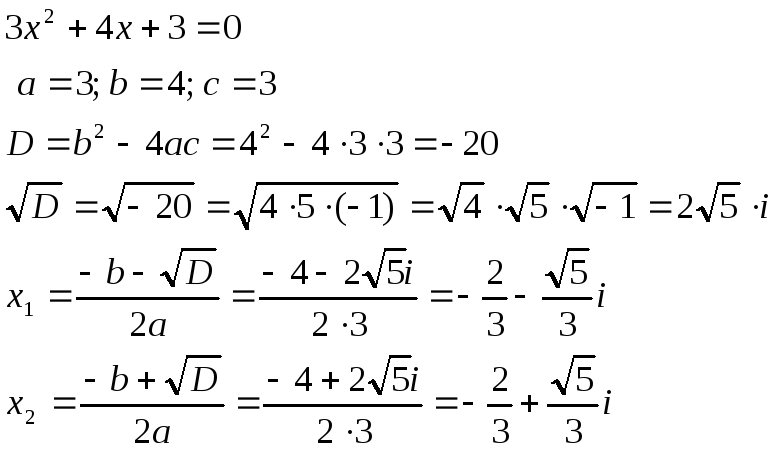риклади. 1. Розв’язати квадратне рівняння:

2. Виконати дії:

а)

б)

Завдання. 1. Розв’язати квадратне рівняння:

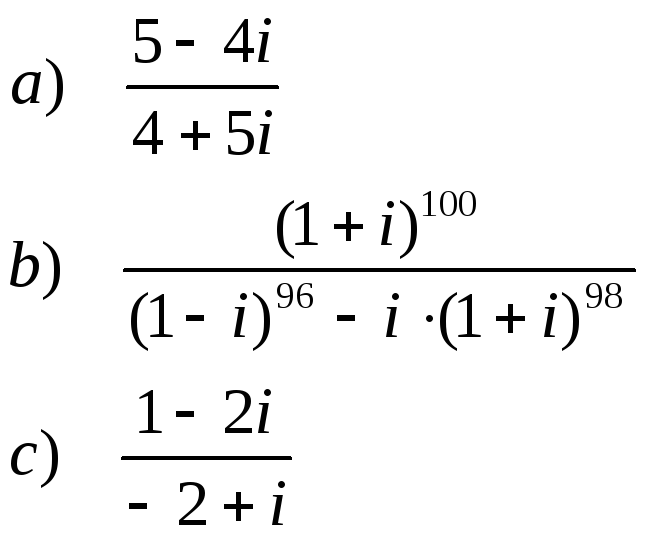
2. Виконати дії:

Контрольні запитання:

1. Яка форма запису комплексного числа називається алгебраїчною?

2. Як записати в алгебраїчній формі дійсні числа?

3. Коли два комплексних числа будуть спряженими?

4. Чому корені квадратного рівняння з від’ємним дискриминантом взаємно спряжені числа?

5. За якими правилами виконуються арифметичні дії над комплексними числами в алгебраїчній формі?

Л ітература: [1] - § 12,13.

Урок № 6

Тема: Дії над комплексними числами в показниковій формі. Розв’язування вправ.

План:

1. Показникова форма комплексного числа.

2. Дії над комплексними числами в показникові формі.

К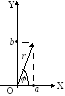ожному комплексному числу можна поставити у відповідність точку координатної площини з координатами (а,b). Таким чином встановлюється взаємно однозначна відповідність між комплексними числами і точками координатної площини. Зображається комплексне число у вигляді вектора, початок якого співпадає з початком координат, а кінець знаходиться в точці (а,b).

Означення: Модулем комплексного числа називається довжина вектора, що зображає дане комплексне число: .

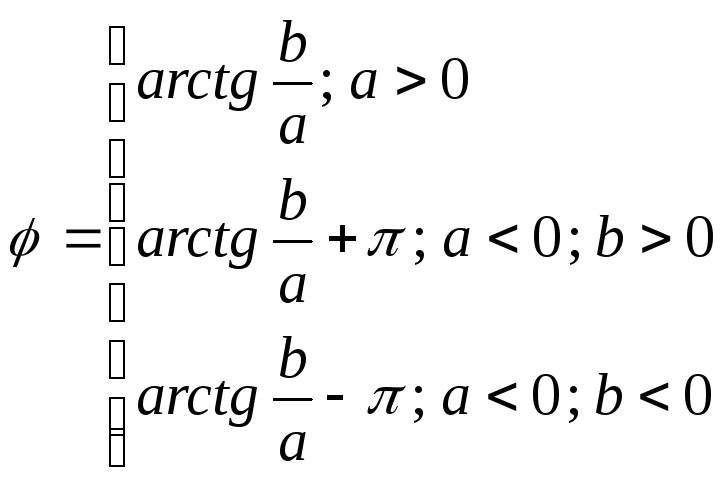Означення: Аргументом комплексного числа називається кут між додатнім напрямком осі Ох і вектором, що зображає дане комплексне число:

Будь-яке комплексне число можна записати у вигляді, який називається тригонометричною формою комплексного числа: .

Можна показати, що вирази та мають одну і ту саму суть. Запис називається показниковою формою комплексного числа.

Додавання та віднімання комплексних чисел в показниковій формі як правило не виконується або виконується геометрично.

Для того щоб помножити два комплексних числа в показниковій формі треба помножити модулі і додати аргументи.

Для того щоб поділити два комплексних числа в показниковій формі треба поділити модулі і відняти аргументи.

Для того щоб піднести комплексне число в показниковій формі до степеню треба до цього степеню піднести модуль і домножити аргумент на показник степеню.

Д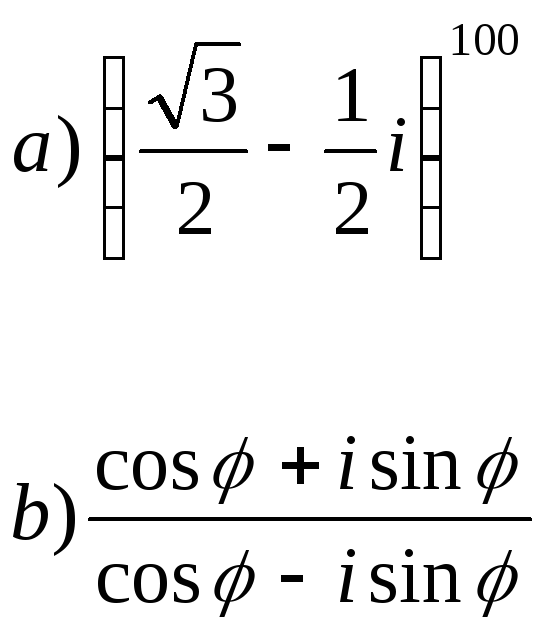обування кореня n-го степеню з комплексного числа в показниковій формі здійснюється за формулою: , де k приймає значення від 0 до n-1.

Приклади. Виконати дії в показниковій формі:

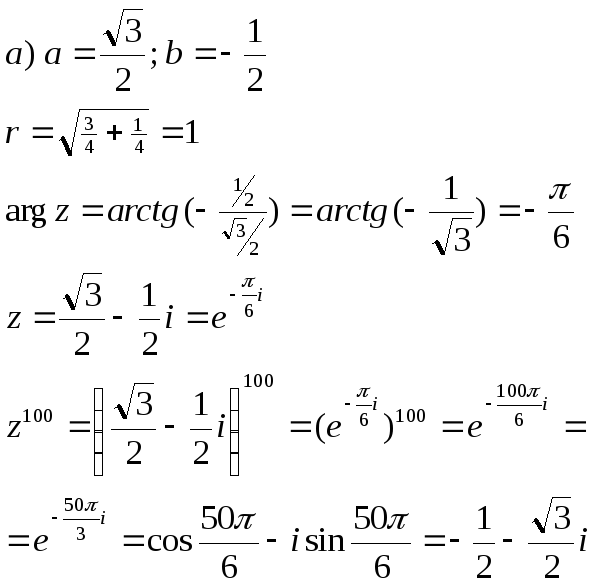
Завдання. Виконати дії в показниковій формі: