3. Абсолютная непрерывность и σ-аддитивность интеграла Лебега

Теорема 1 (абсолютная непрерывность интеграла Лебега).

Пусть – интегрируемая на множестве A функция. Тогда для всех существует , что для всякого измеримого множества такого, что .

Теорема 2 (σ-аддитивность интеграла Лебега).

Пусть f – измеримая функция по множеству A и пусть , – измеримые множества. Тогда f интегрируема по каждому и , причём ряд сходится абсолютно.

Теорема 3. Если , f интегрируема на каждом и ряд сходится, то функция f интегрируема на A и .

4. Предельный переход под знаком интеграла Лебега

Особенно заметны преимущества интеграла Лебега над интегралом Римана, когда мы имеем дело с предельным переходом. В случае интеграла Римана перемена порядка операций интегрирования и перехода к пределу требует установить факт равномерной сходимости последовательности подынтегральных функций. В случае интеграла Лебега подобных трудностей нет. Это вытекает из трёх следующих результатов, играющих центральную роль в теории интегрирования.

Теорема (Лебега о мажорированной сходимости).

Пусть (X,,) – пространство с мерой, и – последовательность измеримых функций, сходящаяся почти всюду к . Если существует интегрируемая функция такая, что (для всех ), то f – интегрируема и

.

Теорема (Беппо-Леви о монотонной сходимости).

Пусть (X,,) – пространство с мерой и , – монотонно возрастающая последовательность интегрируемых функций и пусть существует , что для всех . Тогда почти всюду существует конечный предел , функция f интегрируема и .

Следствие 1. Пусть – последовательность неотрицательных интегрируемых функций и пусть числовой ряд сходится. Тогда почти всюду сходится ряд и

.

Следствие 2. Пусть и пусть f – измеримая функция такая, что существует и ряд сходится. Тогда f интегрируема и .

Теорема (Фату). Пусть (X,,) – пространство с мерой и – последовательность неотрицательных интегрируемых функций, , обладающая свойствами:

1. на X,

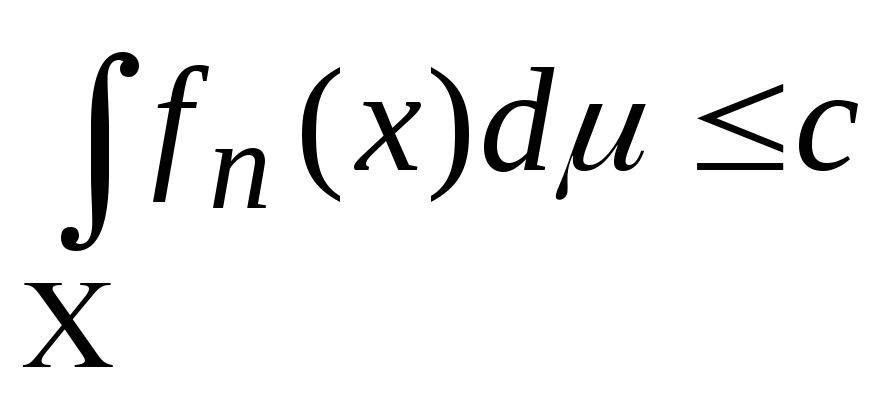2. для всех n.

Тогда функция интегрируема и .

5. Интегрирование по множеству бесконечной меры

Пусть (X,,) – пространство с σ-конечной мерой. В силу определения σ-конечности существует неубывающая последовательность измеримых множеств , для которых для всех k и .

Введём сначала понятие интеграла Лебега по множеству бесконечной меры в случае неотрицательной функции.

Пусть на X и f – измеримая. Поскольку все – измеримы, то имеют смысл и конечны , причём , поэтому существует предел .

Пусть существует и конечен, тогда функция f называется интегрируемой по Лебегу на множестве с σ-конечной мерой и .

Данное определение корректно и не зависит от выбора расширяющейся системы .

Пусть теперь f – измеримая функция произвольного знака. Рассмотрим функции и , тогда , . Функция f называется интегрируемой по Лебегу на X, если на X интегрируемы обе функции и . При этом, по определению .

Нетрудно показать, что для интегрируемости измеримой функции f необходимо и достаточно, чтобы была интегрируема.

Множество X с σ-конечной мерой может быть представлено в виде счётного объединения попарно непересекающихся множеств , т.е. , . В этом случае измеримая функция f называется интегрируемой на X, если сходится ряд . Интегралом Лебега интегрируемой функции f называется число .

Все свойства, установленные для интегралов Лебега по множеству конечной меры, остаются справедливыми и по множеству σ-конечной меры, включая теоремы о предельном переходе.