Тема 4. Интеграл лебега, теоремы о предельном переходе

1. Интеграл Лебега от простой функции

Числовая функция , заданная на измеримом пространстве с конечной мерой , называется простой, если она принимает конечное или счётное число различных значений и является измеримой.

Теорема 1. Функция f является простой тогда и только тогда, когда , где множества измеримы и принимает постоянное значение на множестве , k=1,2,.

Теорема 2. Для любой измеримой функции , заданной на измеримом пространстве (X,,) существует последовательность простых функций, сходящаяся к в каждой точке x. Если функция f ограничена на X, то последовательность можно выбрать равномерно сходящейся. Если , то можно выбрать так, чтобы последовательность была неубывающей.

Пусть – простая функция, принимающая значения , при . Обозначим через , тогда .

Функция f называется интегрируемой по Лебегу, если ряд сходится абсолютно. Если функция f интегрируема, то сумма этого ряда называется интегралом Лебега функции f, т.е.

.

Теорема. Пусть и пусть на каждом B_i функция f принимает значение . Тогда

,

причём функция f интегрируема на X тогда и только тогда, когда ряд сходится абсолютно.

Свойства интеграла Лебега от простой функции.

1. ,

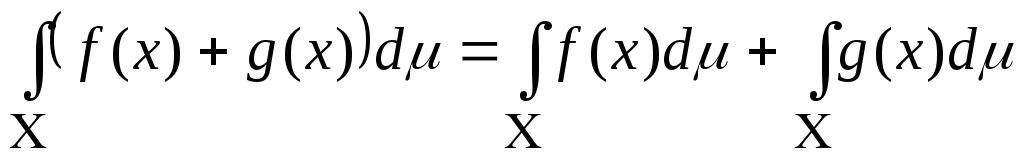причём из существование интегралов в правой части следует существование интеграла в левой;

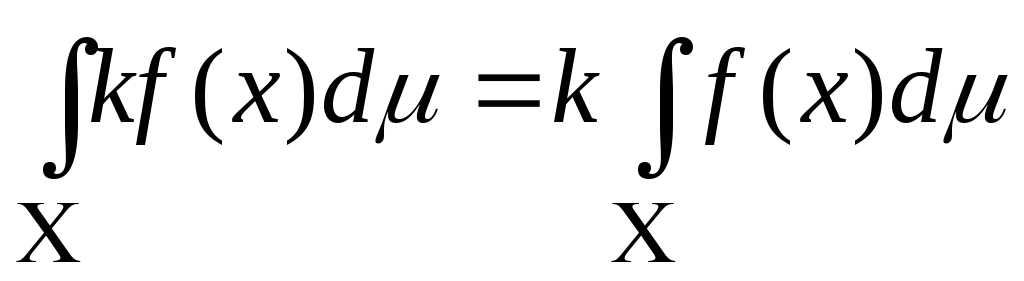2. для всех ,

причём из существование интеграла в правой части следует существование интеграла в левой части;

3) ограниченная на X простая функция f интегрируема на X, причём, если на X, то

.

2. Интеграл Лебега на множестве конечной меры.

Пусть задано (X,,) – пространство с конечной мерой и f : XR измеримая функция.

Определение. Назовём функцию f интегрируемой (суммируемой) на X, если существует последовательность простых интегрируемых на X функций , сходящаяся равномерно к f. Интегралом Лебега функции f на множестве X называется предел интегралов от функций :

.

Различие в определениях интеграла Римана и интеграла Лебега заключается в том, что при составлении интегральных сумм Римана разбиение производится по признаку близости точек на оси OX, а при составлении интегральных сумм Лебега – по признаку близости значений функции.

Основные свойства интеграла Лебега по множеству конечной меры:

1) для любого измеримого множества

;

2) если – интегрируемы по Лебегу, то функция , где , интегрируема по Лебегу и справедливо равенство

;

3) если f – измеримая ограниченная функция, то она интегрируема по Лебегу;

4) если f – интегрируемая функция и , то

;

5) если f – интегрируемая функция и , то

;

6) если – интегрируемые функции и , то

;

7) если , где – интегрируемая, а – измеримая, то f интегрируема по Лебегу;

8) если , где – интегрируемые, а f – измеримая функция, то f – интегрируема.

9) если f – интегрируемая функция, а g – ограниченная измеримая функция, то – интегрируема, причём

.

10) если f интегрируема на X, то f интегрируема на любом измеримом подмножестве из X и

,

(это свойство называется аддитивностью интеграла Лебега);

11) функции f и интегрируемы или неинтегрируемы одновременно, причём справедлива оценка

;

12) если , то ;

13) если почти всюду на X, то ;

14) если почти всюду, то ;

15) если , то почти всюду на X.