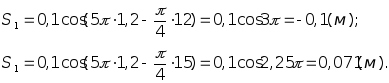Таким образом, период колебаний может быть найден по формуле

.

Произведя вычисления, получим

.

Пример 3. Определить период и частоту колебаний стерня длиной l = 1 м вокруг горизонтальной оси, проходящей через конец стержня (рисунок 2).

Решение. Любое твердое тело, которое может совершать колебания около горизонтальной оси, не проходящей через центр масс, называется физическим маятником.

Период собственных колебаний физического маятника равен

,

где I_z - момент инерции тела относительно оси вращения О_z, а - расстояние от оси вращения до центра масс тела С, m - масса тела, g - ускорение свободного падения.

В рассматриваемой задаче a = l/2, а момент инерции стержня, относительно оси, проходящей через его конец, может быть найден по теореме Штейнера

I_Z = I_C + ma²,

где - момент инерции стержня относительно оси, проходящей через центр масс стержня С.

Таким образом, получаем

.

Период колебаний стерня равен

.

Произведем вычисления

Частота колебаний стержня равна

.

Пример 4. Колебательный контур состоит из конденсатора емкостью С = 8^.10^-9Ф и катушки с индуктивностью L = 2^.10^-3 Гм. На какую длину волны настроен контур?

Решение. Для того чтобы амплитуда колебаний, возникающих в электрическом колебательном контуре под действием электромагнитной волны, была максимальной, частота колебаний в волне должна быть близка к собственной частоте колебаний контура

(1)

Длина электромагнитной волны связана с частотой колебаний соотношений

 = с/, (2)

где с = 3^.10⁸ м/с - скорость распространения электромагнитных волн.

Подставив (1) и (2), получаем

Произведем вычисления: .

Пример5. Методом векторных диаграмм найти сумму двух гармонических колебаний одинакового направления:

x₁=A₁cos(t+₁); x₂=A₂cos(t+₂),

где =3,14 с^-1, А₁=3 см, А₂=4 см, ₁=0, ₂=/2.

Решение. Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени t = 0.

Изобразим векторные диаграммы колебаний х₁ и х₂. Для этого отложим отрезки длиной А₁ = 3 см и А₂ = 4 см под углами ₁ = 0 и ₂ = /2 к оси Ох (рисунок 3).

Векторная диаграмма результирующего колебания х=х₁+х₂ представляет собой векторную сумму диаграмм колебаний х₁ и х₂.

Так как колебания х₁ и х₂ имеют одинаковую частоту, то результирующее колебание будет происходить с той же частотой  и амплитудой А, которую можно найти по теореме косинусов

Так как, по условию задачи,

и

Начальная фаза результирующего колебания равна

Подставив числовые значения, получим

Таким образом, уравнение результирующего колебания имеет вид

x=5cos(3,14t+53⁰), см.

Пример 6. Плоская волна распространяется вдоль прямой со скоростью v = 20 м/с. Две точки, находящиеся на этой прямой на расстояниях х₁ = 12 м и х₂ = 15 м от источника волн, колеблются с разностью фаз  = 0,75. Найти длину волны , написать уравнение волны и найти смещение указанных точек в момент t = 1,2 с, если амплитуда колебаний А = 0,1 м.

Решшение. Точки, находящиеся друг от друга на расстоянии х, колеблются с разностью фаз, равной

Решая это равенство относительно , получаем:

Подставив числовые значения величин, входящих в это выражение, и произведя вычисления, получим

Уравнение плоской волны, распространяющейся вдоль оси Ох, имеет вид

S = Acos(t - kx),

где А = 0,1 м - амплитуда колебаний, (м^-1) - волновое число,

- циклическая частота колебаний.

Таким образом, уравнение волны имеет вид:

S = 0,1cos(5t-/4x) (1)

Чтобы найти смещение S₁ и S₂ точек x₁ и x₂ в момент времени t = 1,2 с достаточно в уравнение (1) подставить значения t и x: