Министерство образования РФ

Брянская Государственная Инженерно-Технологическая Академия

ФИЗИКА

КОЛЕБАНИЯ И ВОЛНЫ. ВОЛНОВАЯ ОПТИКА

Методические указания по выполнению контрольных работ

для студентов инженерно-технических специальностей

Брянск 2001

Министерство образования РФ

Брянская Государственная Инженерно-Технологическая Академия

Кафедра физики

Утверждены научно-

методическим советом БГИТА

протокол № от 2001 г.

ФИЗИКА

КОЛЕБАНИЯ И ВОЛНЫ. ВОЛНОВАЯ ОПТИКА

Методические указания по выполнению контрольных работ

для студентов инженерно-технических специальностей

Брянск 2001

Составители: Вощукова Е.А., к. ф.- м. н., доцент

Симохин С.П., ассистент кафедры физики

Рецензент:

Рекомендовано учебно-методической комиссией

строительного факультета

Протокол № 2001 г.

Основные определения. Законы и Формулы

Уравнение гармонических колебаний

S=Acos(t+₀),

где S - значение колеблющейся величины в момент времени t,

 =2/T=2 - циклическая частота колебаний,

Т - период колебаний,

 =1/T - частота колебаний,

₀ - начальная фаза колебаний.

Период собственных колебаний пружинного маятника

,

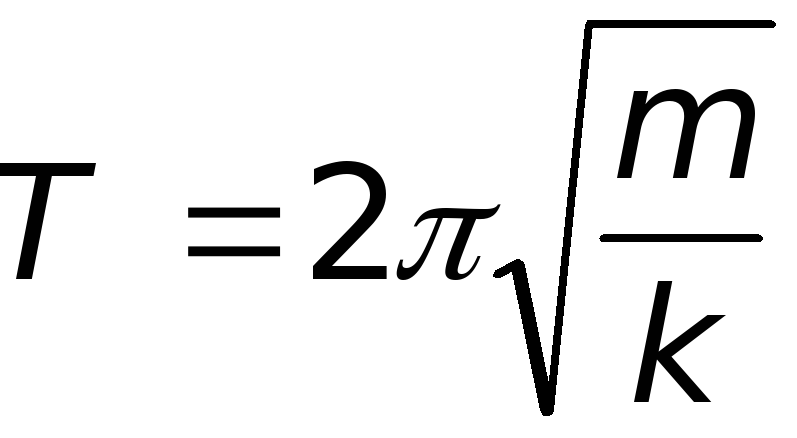где m - масса груза,

k - жесткость пружины.

Период собственных колебаний математического маятника

,

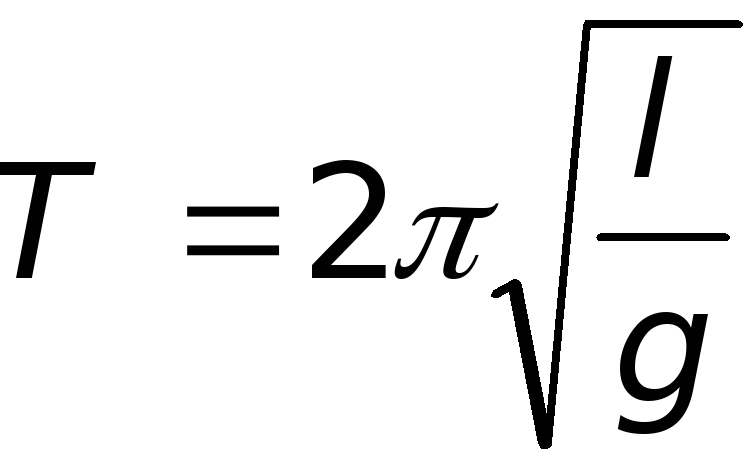где l - длина маятника,

g - ускорение свободного падения.

Период собственных колебаний физического маятника

где I_Z - момент инерции маятника относительно оси вращения,

m - масса маятника,

a - расстояние от оси вращения до центра масса.

Период собственных незатухающих колебаний в электрическом колебательном контуре

где L - индуктивность контура,

С - емкость контура.

При сложении двух одинаково направленных гармонических колебаний с амплитудами А₁ и А₂ и начальными фазами ₁ и ₂ получается гармоническое колебание того же периода с амплитудой

начальной фазой

.

Уравнение плоской гармонической (монохроматической) волны, распространяющийся без затухания вдоль оси Оx

где А - амплитуда колебаний в волне,

 - циклическая частота колебаний,

k = /v = 2/ - волновое число,

v - фазовая скорость волны,

 - длина волны,

₀ - начальная фаза.

Длина волны

Разность фаз колебаний двух точек в волне, находящейся на расстоянии  друг от друга

.

Скорость света в среде с показателем преломления n

где с = 3^.10⁸ м/с - скорость света в вакууме.

Оптическая длина пути световой волны

l_опт = nl,

где n - показатель преломления Среды, l - геометрическая длина пути.

Оптическая разность хода двух световых волн

l_опт=l_опт1-l_опт

Условие интерференции

l_опт = m (m = 0, 1, 2 ...)

Условие минимума интерференции

Оптическая разность хода световых волн, возникающих при отражении монохроматического света от тонкой пленки

где d - толщина пленки,

n - показатель преломления пленки,

i - угол падения света на пленку.

Слагаемые /2 нужно учитывать, если условия отражения света на границах пленки различны (на одной границе отражение происходит от более оптически плотной среды, а на другой - от менее плотной).

Радиус светлых колец Ньютона в отраженном свете

,

где m - номер кольца (m = 1,2,3...),

R - радиус кривизны поверхности линзы,

 - длина световой волны.

Радиус темных колец Ньютон в отраженном свете

(m = 1,2,3,...).

Угол  отклонения лучей, соответствующий максимуму при дифракции на одной цели определяется из условия

где а - ширина щели, m - номер максимума (m = 0, 1, 2, 3,...).

Угол , соответствующий минимуму дифракции на одной щели, определяется из уравнения

(m=1, 2, 3,...).

Формула дифракционной решетки

(m=0, 1, 2,...),

где d - период решетки,

 - угол, под которым наблюдается дифракционный максимум,

m - номер (порядок) максимума.

Закон Брюстера

tgi_Б = n₂₁,

где i_Б - угол падения, при котором отразившийся от границы двух сред луч максимально поляризован;

n₂₁ - относительный показатель преломления основной среды относительно первой.

Закон Малюса

I = I₀cos²,

где I₀ - интенсивность плоскополяризованного света, падающего на анализатор;

I - интенсивность этого света после анализатора;

 - угол между плоскостью колебаний света, падающего на анализатор, и плоскостью пропускания анализатора.

Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:

а)  = []d (в твердых телах), где [] - удельное вращение, d - длина пути, пройденного светом в оптически активном веществе;

б)  = []’сd (в растворах), где с - массовая концентрация оптически активного вещества в растворе.

Примеры решения задач

Пример 1. Частица массой m = 1кг совершает гармонические колебания с частотой  = 10 Гц. В начальный момент времени частица имела максимальное смещение: x_max = 1мм.

Записать уравнение колебаний частицы и начертить их график. Найти координату частицы, скорость, ускорение, кинетическую и потенциальную энергию частицы в момент времени t = 0,05 с.

Решение. Уравнение колебаний частицы можно записать в виде

x=Acos(t+₀), (1)

где А - амплитуда колебаний;

 - циклическая частота;

t - время;

₀ - начальная фаза.

По определению, амплитуда колебаний

A = x_max (2)

Циклическая частота  связана с частотой соотношением

 = 2. (3)

Для момента времени t = 0 формула (1) примет вид:

x_max = Acos₀,

откуда начальная фаза

₀ = arccos(x_max/A) = arccos1,

или ₀ = 0.

С учетом равенств (2) - (4) уравнение колебаний примет вид

х = Acos2t,

где А =1 мм =10^-3м,

 =10 Гц.

График соответствующего гармонического колебания приведен на рисунке 1.

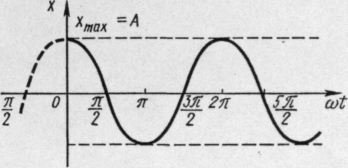
Рисунок 1

Координата частицы в момент времени t=0,05 с равна

х = 10^-3 cos (2 ^. 10 ^. 0,05) = 10^-3.cos = -10^-3 (м)

Зависимость скорости частицы от времени выражается формулой

(5)

Подставив в формулу (5) числовые значения  и А, для момента времени t = 0,05 с получаем

v_x= -2 ^. 3,14 ^. 10 ^. 10^-3sin = 0

Ускорение частицы равно

или для t=0,05 с

Кинетическая энергия частицы

В момент времени t = 0,05 v_x = 0, следовательно Т=0. Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно,

F = -kx,

где k - коэффициент квазиупругой силы.

Потенциальная энергия частицы, движущейся под действием квазиупругой силы, равна

Коэффициент k можно выразить через частоту колебаний:

k = m(2)².

Таким образом. для потенциальной энергии частицы получаем выражение:

.

В момент времени t = 0,05 смещение частицы от положения равновесия равно x = -10^-3 м и, следовательно, потенциальная энергия

.

Пример 2. К пружине подвешен груз массой m = 10кг. Зная, что пружина под влиянием силы F = 10Н растягивается на x = 1,5 см, найти период собственных незатухающих колебаний груза.

Решение. Период собственных колебаний пружинного маятника равен

,

где m - масса груза,

k - жесткость пружины.

Для определения k используем закон Гука:

F=kx