
- •Рабочая программа раздела “Электромагнетизм”
- •Общие методические указания
- •Основные законы и формулы раздела “Электромагнетизм”
- •4. Примеры решения задач
- •В данном случае , так как направление вектора нормали к площади совпадает с направлением вектора магнитной индукции . Подставив (2) в (1), запишем выражение для эдс индукции по модулю
- •Справочные материалы
- •6. Список рекомендуемой литературы
4. Примеры решения задач
Первая
из задач раздела “Электромагнетизм”
посвящена определению
индукции магнитного поля в заданной
точке посредством формул, вытекающих
из закона Био-Савара-Лапласа, с
использованием принципа суперпозиции
магнитных полей. В задачах используются
следующие комбинации проводников с
током: параллельные или перекрещивающиеся
бесконечно длинные проводники, бесконечно
длинный проводник, согнутый под некоторым
углом, бесконечно длинный проводник и
круговой контур, два соосных круговых
контура, отрезок проводника, квадратная
рамка. Возможны и другие аналогичные
комбинации. При решении необходимо
представить рисунок с изображением
векторов индукции магнитного поля,
создаваемых отдельными проводниками
системы, и результирующий вектор
![]() .
Для расчёта отдельных составляющих
.
Для расчёта отдельных составляющих
![]() следует выбрать соответствующую формулу
из номеров (3.6 –3.10).
следует выбрать соответствующую формулу
из номеров (3.6 –3.10).
Пример 4.1. По отрезку прямого провода BC длиной l = 80 см течёт ток I = 50 А. Определить магнитную индукцию поля, создаваемого этим током в точке А, равноудалённой от концов отрезка провода и находящуюся на расстоянии ro = 30 см от его середины.
|
B C |
Решение |
|
|
A I = 50 А ro = 30 см = 0,3 м BA = CA μ = 1 μo = 4π·10-7 Гн/м
|
|
Применим формулу для отрезка проводника с током, вытекающую из закона Био-Савара-Лапласа
При симметричном расположении точки А относительно отрез- ка
провода
|
|
|
||
|
С
учётом (2) формула (1) примет вид:
Из
рисунка следует, что
Подставив
выражение (4) для
Проверку размерностей
в полученной рабочей формуле
производить нет необходимости,
поскольку единственное преобразование
состояло в получении выражения для
Подставим численные значения исходных величин в формулу (5) и произведём соответствующие вычисления
Ответ: BA = 26,7 мкТл
Пример 4.2. По двум бесконечно длинным прямым проводникам, находящимся на расстоянии R = 10 см друг от друга в вакууме, текут токи I1 = 20 А и I2 = 30 А одинакового направления. Определить магнитную индукцию B поля, создаваемого токами, в точках, лежащих на прямой, соединяющей оба провода, если 1) точка C лежит на расстоянии r1 = 2 см левее левого провода; 2) точка D лежит на расстоянии r2 = 3см правее правого провода; 3) точка G лежит на расстоянии r3 = 4 см правее левого провода. |
||
|
|
Решение |
|
|
I2 = 30 А R = 10 см = 0,1 м r1 = 2 см = 0,02 м r2 = 3 см = 0,03 м r3 = 4 см = 0,04 м μ = 1 μo = 4π·10-7 Гн/м
|
B1C I1 B2G I2 B2C C G D
r3 B1G B1D r1 R r2 B2D
Для расчёта магнитной индукции каждого из проводников применим формулу для бесконечно длинного проводника с током
|
|
|
BC - ? BD - ? BG - ? |
|
|
|
Индукцию результирующего
магнитного поля найдём на основании
принципа суперпозиции
магнитных полей
Направление составляющих векторов индукции находим по правилу буравчика. В точке C направления векторов совпадают, следовательно, подставляя в (2) конкретные значения параметров формулы (1), получим
В точке D направления векторов также совпадают, следовательно, имеем
В точке G направления векторов противоположны, следовательно, имеем
Проверку размерностей в полученных рабочих формулах производить нет необходимости в силу отсутствия алгебраических преобразований. Подставим численные значения исходных величин в формулы (3)- (5) и произведём соответствующие вычисления
Аналогично
в точке D
Ответ: ВΣС = 0,25 мТл; ВΣD = 0,23 мТл; ВΣG = 0 |
||
Пример 4.3. Бесконечно длинный проводник с током I = 50 А согнут под прямым углом. Найти напряжённость магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии d = 10 см.
|
|
Решение |
|
|
|
d = 10 см = 0,1 м
|
I
r1 HA A π/4 d π/4 π/4 r2 I 00 |
Изогнутый
провод можно рассматривать как два
полубесконечных отрезка и применить
к ним соответствующую формулу
|
|
|
|
|
||
|
При этом для первого
проводника
Направление составляющих векторов индукции находим по правилу буравчика. В точке А направления векторов совпадают, следовательно, подставляя в (2) конкретные значения параметров формулы (1), получим
Проверку размерностей в полученных рабочих формулах производить нет необходимости в силу отсутствия алгебраических преобразований. Подставим численные значения исходных величин в формулу (3) и произведём соответствующие вычисления
Ответ: HA = 384,46 А/м |
|||
Вторая группа задач основана на применении закона Ампера либо формулы силы Лоренца. Для задач на силу Ампера используются варианты проводника с током, помещённого в однородное магнитное поле, взаимодействия двух проводников с током, трёх проводников с током либо проводника с током и квадратной рамки. Для проводника с током, помещённого в магнитное поле, используется формула (3.12), для двух параллельных проводников – формула (3.13), для трёх параллельных проводников либо проводника и квадратной рамки к формуле (3.13) добавляется принцип суперпозиции сил. Для задач на силу Лоренца используются варианты движения заряженной частицы в однородном магнитном поле по окружности либо по винтовой линии, а также движения заряженной частицы в поле, создаваемом бесконечно длинным проводником с током, индукция которого находится по формуле (3.8). Величина силы Лоренца находится по формуле (3.16); поскольку сила Лоренца перпендикулярна вектору скорости частицы, она сообщает ей центростремительное ускорение. Поэтому для решения задач о движении заряженной частицы в однородном магнитном поле необходимо использовать второй закон Ньютона и формулу центростремительной силы.
Пример 4.4. По трём прямым параллельным проводам, находящимся на одинаковом расстоянии d =20 см друг от друга текут одинаковые токи I = 400А. В двух проводах направления токов совпадают. Вычислить для каждого из проводов отношение силы, действующей на него, к его длине.
|
|
Решение |
|
|
I1 = I2 = I3 = 400 А d12 = d23 = d13 = 20 см = = 0,2 м
|
F3 α3 F32 F31
d13 d23 F12 F21
F13 F1 F2 F23 α1 α2 |
На рисунке изображены силы Ампера, действующие на каждый из проводников со стороны соседних. Проводники 1 и 2, в которых токи текут в одном направлении, притягиваются, проводники 1и 3, 2 и 3, в которых токи текут в |
|
F2 - ? F3 - ? |
||
|
противоположных направлениях, отталкиваются. Силы Ампера взаимодействия двух длинных параллельных проводников находим по формуле
Соответственно сила, действующая на единицу длины проводника, будет находиться как
Результирующая сила, действующая на единицу длины проводника со стороны двух соседних, будет находиться по правилам векторной алгебры
Из треугольников сил очевидно, что F1/l = F12/l = F13/l; F2/l = F21/l = F23/l. Численное значение силы F3/l найдём из теоремы косинусов
где α3 = 120° (cos120° = -0,5). |
||
Проверку размерностей в полученных рабочих формулах производить нет необходимости в силу очевидности алгебраических преобразований.
Найдём численные значения сил
![]() А/м.
А/м.
![]() А/м.
А/м.
Ответ: F1/l = F2/l = 0,16 А/м; F3/l = 0,27 А/м
Пример 4.5. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией В = 0,3 Тл и начал двигаться по окружности. Вычислить радиус окружности.
|
|
Решение |
|
|
mp = 1,67·10-27 кг U = 600 B B = 0,3 Тл |
|
Движение заряженной частицы в однородном магнитном поле происходит по окружности в случае, когда частица влетает в магнитное поле перпендикулярно вектору магнитной индукции. Так как сила Лоренца пер- |
|
R - ? |
||
пендикулярна
вектору скорости
![]() ,
то она сообщает протону нормальное
ускорение
,
то она сообщает протону нормальное
ускорение
![]() .
Согласно
второму закону Ньютона,
.
Согласно
второму закону Ньютона,
![]() .
(1)
.
(1)
Модуль силы Лоренца находится по формуле
![]() ,
(2)
,
(2)
где α = 90о в случае круговой траектории частицы.
Нормальное ускорение находится по формуле
![]() .
(3)
.
(3)
Подставляя (2) и (3) в (1), получим
![]() ,
(4)
,
(4)
откуда радиус траектории протона будет равен
![]() .
(5)
.
(5)
Скорость протона найдём, воспользовавшись связью между работой сил поля и изменением кинетической энергии протона
![]() ,
(6)
,
(6)
откуда скорость протона
![]() .
(7)
.
(7)
Подставляя (7) в (5), получим
![]() .
(8)
.
(8)
Убедимся в том, что правая часть этого равенства даёт единицу длины (м)
![]() .
.
Следовательно, выведенная формула (8) имеет правильный физический смысл. Подставим численные значения в формулу (8)
![]() см.
см.
Ответ: R = 1,18 см
Пример
4.6. Электрон,
имея скорость
![]() =
2 Мм/с, влетел в однородное магнитное
поле с индукцией B
= 30 мТл под
углом α = 30о к
направлению линий индукции. Определить
радиус R
и шаг h
винтовой
линии, по которой будет двигаться
электрон.
=
2 Мм/с, влетел в однородное магнитное
поле с индукцией B
= 30 мТл под
углом α = 30о к
направлению линий индукции. Определить
радиус R
и шаг h
винтовой
линии, по которой будет двигаться
электрон.
|
|
Решение |
|
me = 9,1·10-31 кг
В = 30 мТл = 3·10-2 Тл α = 30о
|
|
|
R - ? h - ?
|
На
заряженную частицу
(в нашем
случае электрон), влетевшую в магнитное
поле, действует сила Лоренца,
перпендикулярная векторам магнитной
индукции
![]() и скорости
и скорости
![]() частицы:
частицы:
![]() .
(1)
.
(1)
Так как вектор силы Лоренца перпендикулярен вектору скорости, то модуль скорости не будет изменяться под действием этой силы. Поэтому и значение силы Лоренца будет оставаться постоянным, как это следует из формулы (1). Из механики известно, что постоянная по величине сила, перпендикулярная вектору скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле под углом к вектору индукции, будет одновременно двигаться по окружности со скоростью v⊥ = v•sinα и прямолинейно вдоль поля со скоростью vǁ = v•cosα. В результате одновременного участия в этих двух движениях траектория электрона будет представлять винтовую линию (см. рисунок).
Радиус окружности, по которой движется электрон, найдём, приравнивая силу Лоренца (1) к центростремительной силе (2)
![]() .
(2)
.
(2)
Приравнивая правые части уравнений (1) и (2), получим
![]() ,
(3)
,
(3)
откуда радиус окружности, описываемой электроном,
![]() .
(4)
.
(4)
Период обращения электрона по окружности
![]() .
(5)
.
(5)
Шаг винтовой линии равен пути, проходимому электроном вдоль поля со скоростью vx за период
![]() .
(6)
.
(6)
Подставив числовые значения, получим
![]() =
0,19 мм;
=
0,19 мм;
![]() мм.
= 2,06 мм.
мм.
= 2,06 мм.
Ответ: R =0,19 мм; h = 2,06 мм
Третья из задач посвящена явлению электромагнитной индукции и описывающему это явление закону Фарадея (3.23). В задачах этой группы используются различные способы изменения магнитного потока, пронизывающего контур или катушку. В одних вариантах задаётся закон изменения магнитного потока Φ (индукции В, напряжённости магнитного поля Н), пронизывающих неподвижный контур или катушку. Закон может быть линейным или синусоидальным, и представлен либо уравнением, либо графически. В случае графического представления необходимо по заданной зависимости составить соответствующее ему уравнение. Напряжённость магнитного поля Н переводится в индукцию В с помощью формулы (3.1), индукция В - в магнитный поток Φ с помощью формулы (3.19); выражение для магнитного потока подставляется в закон Фарадея (3.23), после чего выполняется операция дифференцирования магнитного потока по времени.
В задачах на два соосных контура по заданному закону изменения тока в большом контуре необходимо найти закон изменения магнитного потока, пронизывающего малый контур с помощью формулы (3.6).
В других вариантах магнитное поле постоянно, а в нём рамка либо вращается, либо растягивается так, что её площадь обращается в ноль. Возможны варианты, когда требуется определить разность потенциалов (напряжение) на концах проводящего стержня, движущегося поступательно или вращающегося в магнитном поле. В задачах этого типа необходимо найти закон изменения площади S(t) и подставить его формулу магнитного потока (3.19); последующий порядок расчёта совпадает с рассмотренным выше.
В случае протекания через индуктивную катушку изменяющегося тока возникает явление самоиндукции; в данном случае следует пользоваться формулой (3.27).
Пример 4.7. В однородном магнитном поле с индукцией В = 0,02 Тл равномерно вращается с частотой n = 300 оборотов в минуту вокруг вертикальной оси горизонтальный стержень длиной l = 0,5 м. Ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Определить разность потенциалов U на концах стержня.
|
|
Решение |
|
|
l l = 0,5 м α = 0°
|
|
Разность потенциалов U, возникающая на концах стержня, будет равняться ЭДС индукции ℰi, определяемой в соответ- ствии с законом Фарадея |
|
U - ? |
||
ℰi
=
![]() .
(1)
.
(1)
Магнитный поток в общем случае находится как
![]() .
(2)
.
(2)


 Дано
Дано
 BA
- ?
BA
- ? .
(4)
.
(4)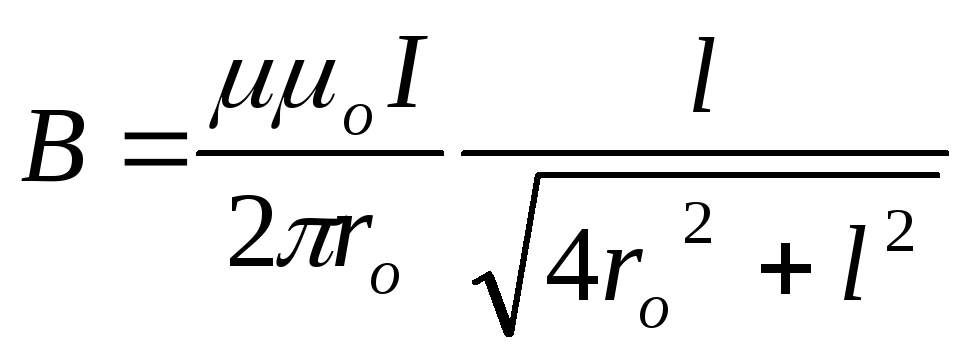 .
(5)
.
(5) Дано
Дано I
I 1
=
20 А
1
=
20 А Дано
Дано


 I
=
50 А
I
=
50 А
 HA
- ?
HA
- ?
 Дано
Дано F1
- ?
F1
- ? Дано
Дано qp
= 1,6·10-19
Кл
qp
= 1,6·10-19
Кл
 Дано
Дано

 Дано
Дано В
= 0,02 Тл
В
= 0,02 Тл
