Утверждение 3.

Координаты вектора в базисе e равны сумме координат векторов . Координаты вектора в базисе e равны координатам вектора , умноженным на .

Следствие. Координаты линейной комбинации векторов равны линейным комбинациям координат векторов.

Утверждение 4.

В n-мерном линейном пространстве любая упорядоченная линейно независимая система из n векторов является базисом.

Если – базис в , то равенство

возможно лишь тогда, когда , т.е. система

,

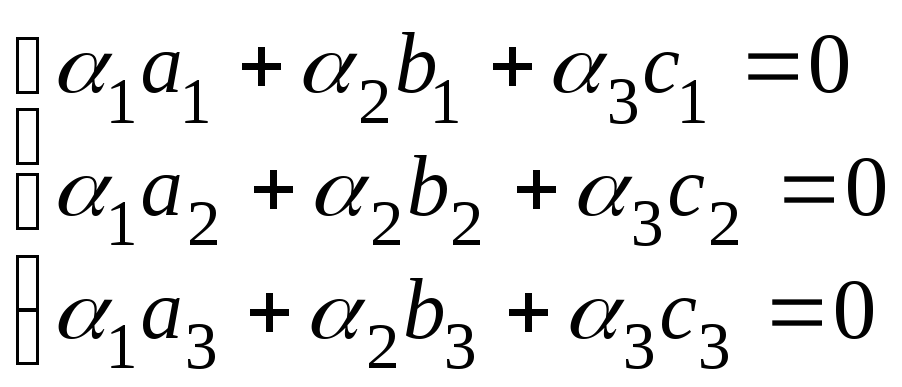где – координаты векторов в базисе соответственно, должна иметь единственное решение. Тогда получаем условие линейной независимости трех векторов:

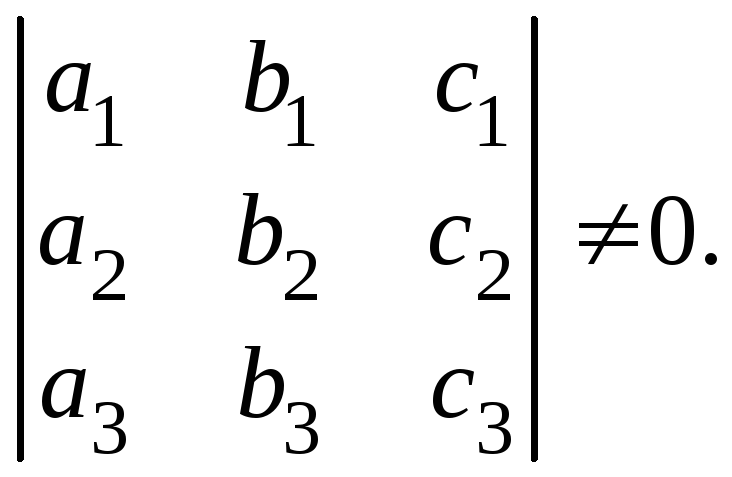
Если векторы образуют базис в , то по определению базиса любой вектор можно представить в виде:

или, в координатной записи:

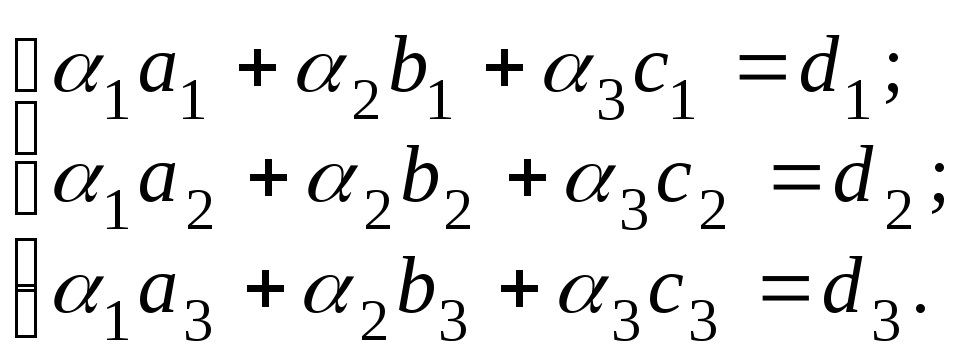
Числа называются координатами вектора в базисе .

4. Координаты вектора. Координатная запись вектора

Рассмотрим декартову систему координат, т.е. три взаимно перпендикулярных, пересекающихся в точке 0 оси 0х, 0у, 0z. Пусть – единичные направляющие векторы этих осей и – произвольный вектор. Покажем, что векторы образуют базис. Отложим вектор от начала координат, пусть М – конец вектора , т.е. (рис. 5). Обозначим – проекции вектора на оси координат, – проекции точки М на оси координат, – проекцию точки М на плоскость . Тогда, по определению произведения вектора на число, получаем (рис. 5):

.

По определению сложения и равенства векторов

следовательно:

Проекции вектора на оси координат называются координатами вектора. Таким образом, координатная запись вектора имеет вид:

. (4)

Откуда следует, что – базис.

Довольно часто вектор задается перечислением его координат, т.е. запись имеет вид: или (первая запись является более строгой, но чаще используется вторая).

Пусть , проекция точки А на ось 0x имеет координату , а проекция точки В – координату , тогда по определению проекции вектора на ось

Следовательно, если

то

Из доказанных свойств проекций вектора на ось получаем правила сложения и умножения вектора на число в координатной форме:

По теореме Пифагора находим длину вектора (рис. 5):

(5)

И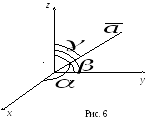 з определения произведения вектора на число следует, что если ненулевые коллинеарные векторы, то такое, что или

.

Отсюда получаем условие коллинеарности векторов, заданных своими координатам:

. (6)

Пусть – углы, которые вектор составляет с осями координат (рис. 6), тогда по формуле (1)

Возведя в квадрат эти равенства и сложив их, получим:

.

Кроме того, , т.е.

,

где – направляющие косинусы вектора . Координаты единичного вектора равны направляющим косинусам.

5. Скалярное произведение векторов и его свойства

Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначение: или .

Таким образом, по определению

, (7)

где угол между векторами. По формуле (1)

т.е.

(8)

Свойства скалярного произведения векторов (ненулевые векторы)

. прямой угол (),

острый угол,

тупой угол;

2^о.

3^о.

4^o.

Если , то по определению

Произведение называется скалярным квадратом вектора

Получим формулу для вычисления скалярного произведения через координаты сомножителей. Пусть , тогда, используя доказанные свойства l° – 4°, получаем:

(свойство 1^о),

( единичные векторы).

Таким образом, скалярное произведение векторов равно сумме попарных произведений соответствующих координат этих векторов:

(9)

Основные приложения скалярного произведения

1. Вычисление угла между векторами