Питання для самоперевірки

1. Який многочлен називається інтерполяційним?

2. Як записується многочлен Лагранжа?

3. Яка погрішність інтерполяційного многочлена?

4. Як виводиться інтерполяційний многочлен Лагранжа для рівновіддалених вузлів?

5. В якому випадку використовується фаза інтерполяції?

6. Що називається кінцевою різницею функції 1-го і 2-го порядку?

7. Як будуються многочлени Ньютона для інтерполяції «вперед» та «назад »через х ?

8. Як будуються многочлени Ньютона для інтерполяції «вперед» та «назад »через ?

9. Що вибирається за початок відліку у формулах для інтерполяції «назад»?

Використовувана література

1. [1] стор. 27-37;стор. 43-55

2. [2] стор. 109-118

3. [3] стор. 6-15

7. ЛЕКЦІЯ 7. РІШЕННЯ ЗАДАЧ ЛІНІЙНОГО

ПРОГРАМУВАННЯ.

План лекції

1. Постановка задачі.

2. Геометричний метод рішення.

3. Симплексний метод рішення.

7.1 Постановка задачі.

Лінійне програмування - наука, що вивчає методи перебування мінімального і максимального значень лінійної функції, на невідомі який накладені лінійні обмеження.

Розглянемо лінійну функцію: (7.1)

Така функція називається цільовою функцією. Нехай на невідомі функції накладені обмеження:

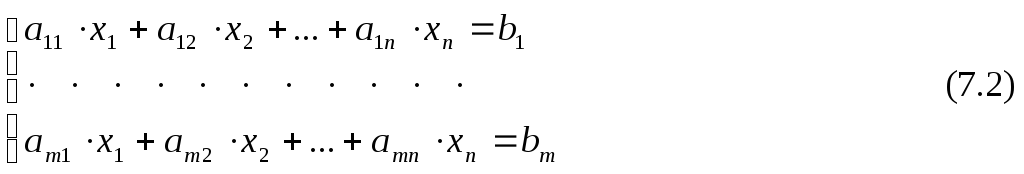
Потрібно знайти такий набір значень невідомих , який задовольняв би системі (7.2) і мінімізував (максимізував) функцію мети.

Виз. Безліч значень X , що задовольняє системі обмежень (7.2), називається областю припустимих рішень. Рішення з цієї області називається планом. У векторному виді задача лінійного програмування виглядає в такий спосіб.

Нехай треба мінімізувати (максимізувати) лінійну форму: при обмеженнях: ; де ,

,…, , (7.3)

Виз. План називається опорним, якщо серед векторів

векторів лінійно незалежні.

Виз. Оптимальним називається план, що задовольняє системі (7.2) і мінімізує (максимізує) функцію мети.

У реальних задачах система обмежень може містити нерівності. Тоді система обмежень має вид:

Геометрично перші обмеження являють собою на півплощини.

7.2 Геометричний метод рішення.

Цей метод використовується у випадку двох перемінних: и (на площині). Нехай потрібно мінімізувати (максимізувати) лінійну функцію: при обмеженнях:

Геометрично перші обмеження являють собою напівплощини

з граничною прямою . Обмеження, що залишилися - прямі. Областю припустимих рішень є їхнє перетинання. Область припустимих рішень може являти собою замкнутий чи відкритий багатокутник, промінь, крапку і т.д. Нехай безліч припустимих рішень - обмежений замкнутий багатокутник. Лініями рівня цільової функції є набір рівнобіжних прямих. Значення функції зростає в напрямку градієнта, убуває в напрямку антиградієнта. Будуємо лінію з нульовим рівнем: . У випадку мінімізації функції мети будемо пересувати цю лінію паралельно самої собі в напрямку антиградієнта таким чином, щоб вона перетиналася з областю припустимих рішень. Тоді крайнє положення, що займе ця лінія визначає точку мінімуму. При рішенні задачі максимізації нульову лінію рівня треба переміщати в напрямку градієнта.

Приклад7.1.

Фірма робить 2 моделі книжкових полиць. Виробництво обмежене наявністю сировини і часом машинної обробки. Для кожного виробу моделі А потрібно Фірма робить 2 моделі книжкових полиць. Виробництво обмежене наявністю сировини і часом машинної обробки. Для кожного виробу моделі А потрібно 3 м² дощок, для В – 4 м². Фірма одержує до 1700 м² дощок у тиждень. Для кожного виробу А потрібно 12 хвилин машинного часу, для В - 30 хвилин. У тиждень можна використовувати не більш

160 годин. Скільки виробів кожної моделі треба зробити за тиждень, щоб одержати максимальний прибуток, якщо одиниця виробу типу А дає прибуток -; одиниця виробу типу В-.

Рішення.

- кількість виробів типу А;

- кількість виробів типу В.

Функція мети - прибуток при реалізації усіх виробів.

2 обмеження:

1- на використання матеріалів (дощок)

2- на час машинної обробки

,

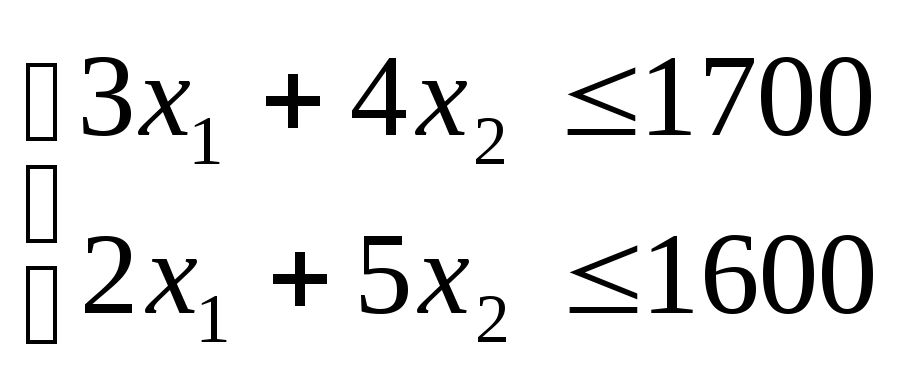Кожне обмеження геометрично є напівплощиною.

Граничні лінії:

Побудуємо на графіку область допустимих рішень.

Областю припустимих рішень є чотирикутник .

Градієнт функції мети:

Будуємо лінію з нульовим рівнем: ;

Пересуваючи нульову лінію рівня таким чином, щоб вона перетиналася з областю припустимих рішень, одержимо, що крайній є точка С - це точка максимуму. Знайдемо її координати, вирішуючи систему:

максимальний прибуток