3.3 Побудова квадратичної моделі.

Потрібно за результатами експериментів побудувати квадратичну модель . Розглянемо функцію :

Щоб знайти мінімальне значення цієї функції, обчислимо частки похідні й дорівняємо їх нулю. Одержимо систему рівнянь.

Розкриваючи дужки, одержимо

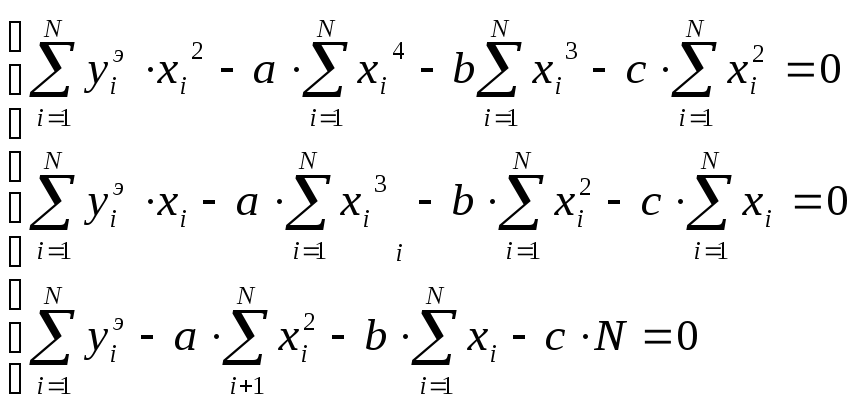
Для зручності обчислень, занесемо вихідні дані й розрахунки в таблицю.

i
1
…
N

Вирішуючи систему щодо коефіцієнтів, , , одержуємо шукане рівняння моделі.

Приклад 3.2.

Побудуємо квадратичну модель по заданим у Прикладу 3.1 даним експерименту

1) Знайдемо коефіцієнти квадратичної моделі методом найменших квадратів. Треба по зазначеної формулі підібрати коефіцієнти моделі , , .

Побудуємо таблицю:

n
1	-1.8	3.24	1.6	-2.88	-5.832	10.4976	5.184
2	0.4	0.16	1	0.4	0.064	0,0256	0.16
3	0.6	0.36	0.8	0.48	0.216	0.1296	0.288
4	2	4	0.6	1.2	8	16	2.4
5	2.9	8.41	0.5	1.45	24.389	70.728	4.205
	4.1	16.17	4.5	0.65	26.837	97.3809	12.237

Отримуємо систему

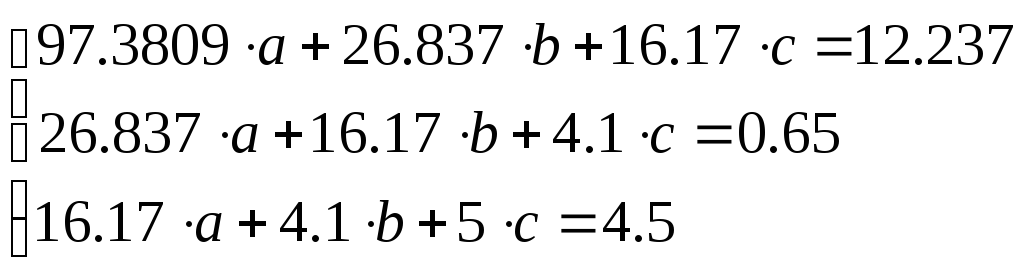
Вирішуючи систему , знайдемо коефіцієнти:

= 0.03076

= - 0.272928

= 1.02432

Зазначена залежність

2) Знайти відхилення експериментальних результатів від результатів, отриманих по моделі

вихідні дані		результат
-1.8	1.6	1.615425	0.00158
0.4	1	0.99607	0.002789
0.6	0.8	0.87562	0.003527
2	0.6	0.602714	0.0001287
2.9	0.5	0.49458	0.0005741
			0.086008

визначаються по моделі шляхом підстановки табличних значень із першого стовпця замість х у рівняння моделі

= 0.03076(-1.8)²- 0.272928(-1.8)+1.02432 =1.615425 ………………………………………………….

= 0.03076 (0.4)²- 0.272928(0.4)+1.02432 =0.99607

Відхилення:

...........................................................................

3) Побудуємо графік, застосовує

х		x*x	x*x*x	x*x*x*x	x*y	x*x*y
-1,8	1,6	3,24	-5,832	10,4976	-2,88	5,184	1,6153	0,00023
0,4	1	0,16	0,064	0,0256	0,4	0,16	0,9201	0,00638
0,6	0,8	0,36	0,216	0,1296	0,48	0,288	0,8716	0,00513
2	0,6	4	8	16	1,2	2,4	0,6015	2,26E-06
2,9	0,5	8,41	24,389	70,7281	1,45	4,205	0,4915	7,19E-05
4,1	4,5	16,17	26,837	97,3809	0,65	12,24		0,011827