4 Построение теней
При оформлении чертежей фасадов зданий или других архитектурных сооружений возникает необходимость придать изображаемому предмету объемность, рельефность форм, т.е. придать чертежу наглядность и выразительность. Это достигается благодаря наличию светотени, полученной в результате освещения здания или сооружения солнечными лучами.
Изображение на чертежах теней, в полной мере соответствует реальной действительности, поэтому является относительно сложной задачей.
В практике проектирования, с целью упрощения построения теней, принимается ряд условных положений, а именно:
- освещенные тела сами не являются источником света;
- пределом распространения светового луча является первая, встретившаяся на его пути материальная точка;
- воздействие воздушной среды не учитывается.
При этих условиях все задачи на построение теней решаются с помощью способов начертательной геометрии.
Введем следующие дополнительные обозначения:
L – источник света (солнце, лампа и т.д.);
l - световой луч;
A1t, B!t ,α1t – падающие тени точек, линий и плоскостей на горизонтальную плоскость проекций;
A2t, B2t,α2t – падающие тени точек, линий и плоскостей на фронтальную плоскость проекций.
Изображение теней на архитектурно-строительных чертежах могут быть построены как при искусственном (лампа, свеча и т.п.), так и при естественном (солнце) источнике света.
При искусственном освещении источник света принимается за светящуюся точку L. При естественном, т.е. при солнечном освещении, световые лучи l принимаются параллельными друг другу т.к. источник света (солнце) бесконечно удален (рисунок 4.1).
Если на пути световых лучей прямолинейно по всем направлениям встретится какое-либо непрозрачное тело, например сфера, то поверхность этого тела, обращенная к источнику света, будет освещена. Неосвещенный участок поверхности тела, расположенный с другой стороны от источника света является собственной тенью. Итак, собственной тенью предмета называется совокупность неосвещенных элементов части поверхности этого предмета, обращенной в противоположную от источника света сторону.
Граница между освещенной частью поверхности предмета и частью, находящейся в собственной тени, называется контуром собственной тени. В соответствии с рисунком 4.1 – это замкнутая линия ABCD.
Любое освещенное тело обязательно будет отбрасывать свою тень на какую-либо плоскость или на другой предмет. Эта тень будет называться падающей тенью (A′B′C′D′).
Если само тело уже находится в теневом пространстве, то оно не будет иметь собственную и падающую тень, т.к. само оно находится в зоне падающей тени от другого предмета.
В обоих случаях контур собственной тени определяется как линия касания обертывающей конической или цилиндрической поверхности, а контур падающей тени – как линия пересечения этой поверхности с плоскостью П1.
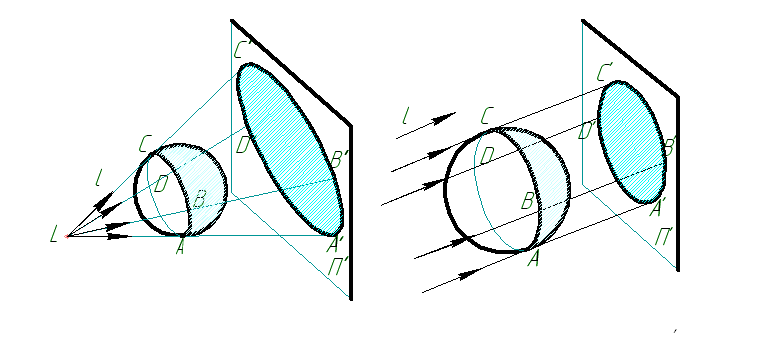
Рисунок 4.1
Решения задач в построении теней сводится к определению контуров собственных и падающих теней. Контур падающей тени от поверхности является тенью от контура собственной тени, поэтому по контуру падающей тени можно определить контур собственной тени, и наоборот. Контуры собственных и падающих теней гранных поверхностей получаются в виде замкнутых ломаных линий, тени криволинейных поверхностей – кривые замкнутые линии.
На архитектурно-строительных чертежах построение теней выполняется в основном при параллельном направлении световых лучей, что соответствует условиям естественного освещения.