
- •Введение
- •1 Теоретические основы
- •Основные обозначения
- •1.2 Способы проецирования
- •1.2.1 Центральное проецирование
- •1.2.2 Параллельное проецирование
- •1.2.3 Ортогональное проецирование
- •1.2.4 Образование двух- и трёхкартинного комплексного чертежа
- •1.2.4.1 Конкурирующие точки
- •1.3 Ортогональные проекции геометрических объектов и позиционные
- •1.3.1 Изображение прямой линии на комплексном чертеже
- •Р исунок 1.3.1 – Положение прямой относительно плоскостей проекций
- •1.3.1.1 Прямые частного положения
- •1.3.1.2 Следы прямой линии
- •1.3.1.3 Определение натуральной величины отрезка прямой
- •1.3.1.4 Взаимное положение двух прямых
- •1.3.1.5 Теорема о проецировании прямого угла
- •1.3.2 Изображение плоскости на комплексном чертеже
- •1.3.2.1 Главные линии плоскости
- •1.3.2.2 Взаимопринадлежность (инцидентность) точки и плоскости
- •1.3.2.3 Следы плоскости
- •1.3.2.4 Плоскости частного положения
- •1.3.2.5 Параллельность прямой и плоскости
- •1.3.2.6 Параллельность плоскостей
- •1.3.2.7 Перпендикулярность прямой и плоскости
- •1.3.2.8 Пересечение прямой линии с плоскостью
- •1.3.2.9 Пересечение двух плоскостей
- •1.3.3 Кривые линии
- •1.3.3.1 Проекционные свойства плоских кривых
- •1.3.3.2 Ортогональная проекция окружности
- •1.3.4 Образование, задание и изображение поверхностей
- •1.3.4.1 Линейчатые поверхности
- •1 .3.4.2 Коническая и цилиндрическая поверхности
- •1.3.4.3 Поверхности вращения
- •1.3.4.4 Поверхности вращения второго порядка
- •1.3.4.5 Пересечение поверхности с плоскостью
- •1.3.4.6 Конические сечения
- •1.3.4.7 Пересечение поверхностей
- •1.3.4.7.1 Общий алгоритм решения задачи
- •1.3.4.7.2 Примеры пересечения поверхностей
- •1.3.4.7.3 Особые случаи пересечения поверхностей второго порядка
- •1.4 Преобразование комплексного чертежа
- •1.4.1 Способ замены плоскостей проекций
- •1.4.2 Основные задачи, решаемые способом замены плоскостей проекций
- •1.4.3 Способ плоскопараллельного перемещения
- •1.4.4 Способ вращения
- •1.4.4.1 Способ вращения вокруг проецирующей оси
- •1.4.4.2 Основные задачи, решаемые способом вращения
- •1.5 Построение разверток
- •1.5.1 Развертка поверхностей многогранников
- •1.5.1.1 Развертка поверхности призмы
- •1.5.1.2 Развертка поверхности пирамиды
- •1.5.2 Развертка развертываемых кривых поверхностей
- •1.5.2.1 Развертка цилиндрической поверхности
- •1.5.2.2 Развертка конической поверхности
- •2. Геометрические модели в параллельных аксонометрических проекциях
- •2.1 Аксонометрические проекции
- •2.2 Стандартные аксонометрические системы
- •2.3 Аксонометрическая проекция окружности
- •3 Перспективные проекции
- •3.1 Линейная перспектива
- •3.2 Элементы аппарата проецирования
- •3.3 Перспектива точки
- •3.4 Перспектива прямой линии
- •3.5 Построение перспективы способом архитекторов
- •3.5.1 Выбор положения картинной плоскости и точки зрения
- •3.5.2 Построение перспективы с двумя точками схода
- •3.5.3 Построение перспективы с одной точкой схода
- •4 Построение теней
- •4.1 Построение теней в ортогональных проекциях
- •4.1.1 Тень от точки
- •4.1.2 Тень от прямой
- •4.1.3 Тень плоской фигуры
- •4.1.4 Тени геометрических тел
- •4.1.5 Способ обратных лучей
- •4.2 Тени в аксонометрических проекциях
- •4.2.1 Тень от точки и прямой
- •4.2.2 Тени геометрических тел
- •4.3 Тени в перспективе
- •4.3.1 Тени от точки
- •4.3.2 Тень от прямой
- •4.3.3 Тень от поверхности
3.5.2 Построение перспективы с двумя точками схода
Исходными данными для построения перспективы является ортогональные проекции данного объекта и положение линии горизонта.
Построение перспективы зданий производится с одной или двумя точками схода. Рассмотрим пример построения перспективы схематизированного здания с одной точкой схода (рисунок 3.5.2).
Ребра здания, в этом случае, являются вертикальными или горизонтальными прямыми. Для каждой группы взаимно параллельных прямых на плане определяются точки схода F1+ и F1 – в соответствии с рисунком 3.5.1. Эти точки получены на пересечении с основанием картины прямых, приведенных из S1 параллельно соответствующим прямым на плане. Точки 11,21 и 31 пересечения продолжения прямых с основанием картины, являются картинными следами этих прямых.
При построении перспективы в первую очередь строиться вначале перспектива плана. Для этого на свободном поле чертежа проводятся линия основания картины ОО, линия горизонта h, высота которой взята из фронтальной проекции здания и задается главная точка картины P. При этом перспектива может быть построена в любом масштабе по отношению к ортогональным проекциям. Главная ось картины РР1 выбирается так, чтобы обе точки схода, по возможности, поместились в пределах чертежа. С ортогонального чертежа на основание картины в перспективе переносятся картинные следы прямых плана ( точки 11,21,31), а на линию горизонта – точки схода (F1+ и F1-). Расстояния между точками в перспективе должны соответствовать их расстоянию в ортогональных проекциях или увеличены, если принимается масштаб увеличения. Соединив картинные следы (т. 1,2,3) с соответствующими точками схода (F1+ и F1 -), получим перспективу прямых плана и контур перспективы плана (рисунок 3.5.2).
Для построения перспективы вертикальных ребер через все вершины перспективы плана проводятся вертикальные прямые. Ребро, проходящее через точку 21, лежит в картинной плоскости, следовательно, в перспективе оно изобразится в натуральную величину (с учетом масштаба при выполнении перспективы). Через верхнюю точку ребра проводятся прямые в точки схода F1+ и F1 -.
Высота остальных вертикальных прямых определяется до точки пересечения лучей, идущих в точки схода. Эти прямые будут определять положение крайних вертикальных ребер здания в перспективе. Вершины этих ребер соединяются с точками схода, и в пересечении этих лучей определяется положение вершины дальнего ребра здания.
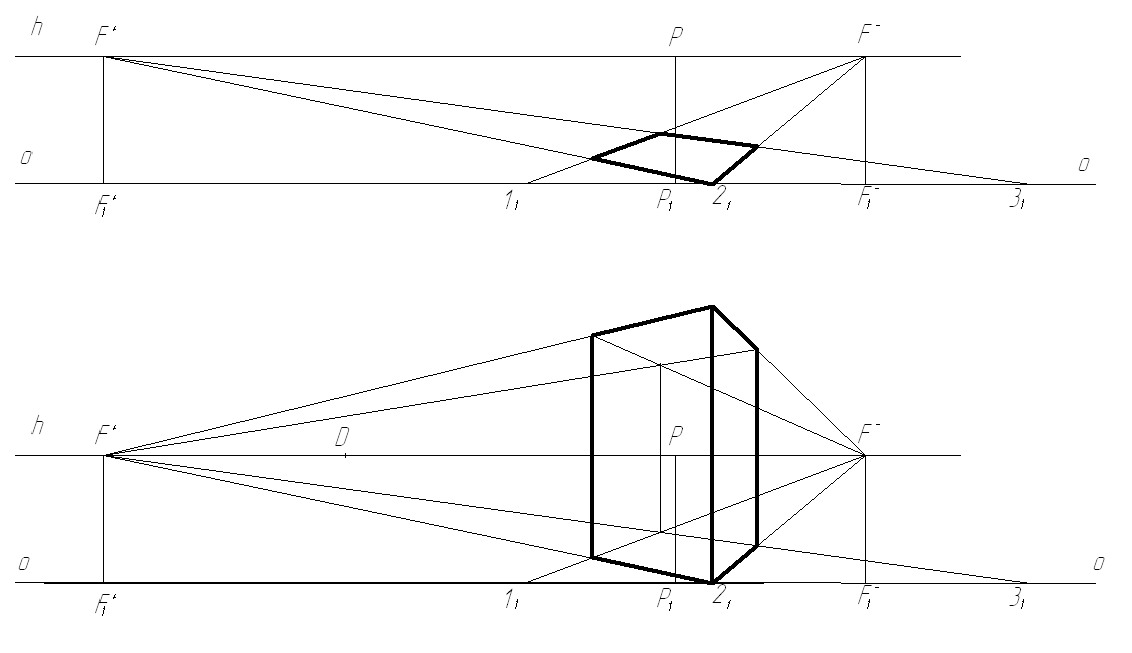
Рисунок 3.5.2 – Построение перспективы схематизированного здания способом архитекторов с одной точкой схода
3.5.3 Построение перспективы с одной точкой схода
В практике построения перспектив, особенно больших размеров, часто приходится ограничиваться использованием лишь одной точки схода. При этом для определения положения ребер здания в перспективе применяется метод масштаба высот.
На данном примере построена перспектива того же объекта с использованием одной точкой схода F -, ближайшей к главной точке картины (рисунок 3.5.4).
В этом случае на подготовительном этапе построения перспективы все точки на плане соединяются с точкой стояния S1 и определяются точки пересечения этих прямых с основанием картины (т.21,31,51). Также находятся картинные следы прямых для правой точки схода (т.11,41).
В соответствии с рисунком 3.5.3 с ортогональных проекций полученные точки переносятся на перспективу с условиями, описанными в предыдущем способе. Для построения в перспективе плана нижней точки крайнего левого ребра схематизированного здания необходимо из точки 21 восстановить перпендикуляр к картинной плоскости до пересечения с лучом, идущим из точки 11. Определяем положение верхней точки ребра в перспективе, отложив из точки 11 его натуральную величину (с учетом масштаба изображения), взятую из фронтальной проекции здания. Соединив верхнюю точку построенной прямой с правой точкой схода F-, находим точку пересечения этого луча с перпендикуляром, проведенным из точки 21 к основанию картины. Соединив верхнюю и нижнюю точки ребра, получим его перспективное изображение. По аналогии выстраивается крайнее правое и дальнее вертикальные ребра, имея в виду, что ближнее к нам ребро находится непосредственно в картинной плоскости, следовательно, спроецировалось в перспективе в натуральную величину. Осталось соединить верхние точки ребер здания и обвести видимые его контуры в соответствии с рисунком 3.5.4. Перспектива построена.
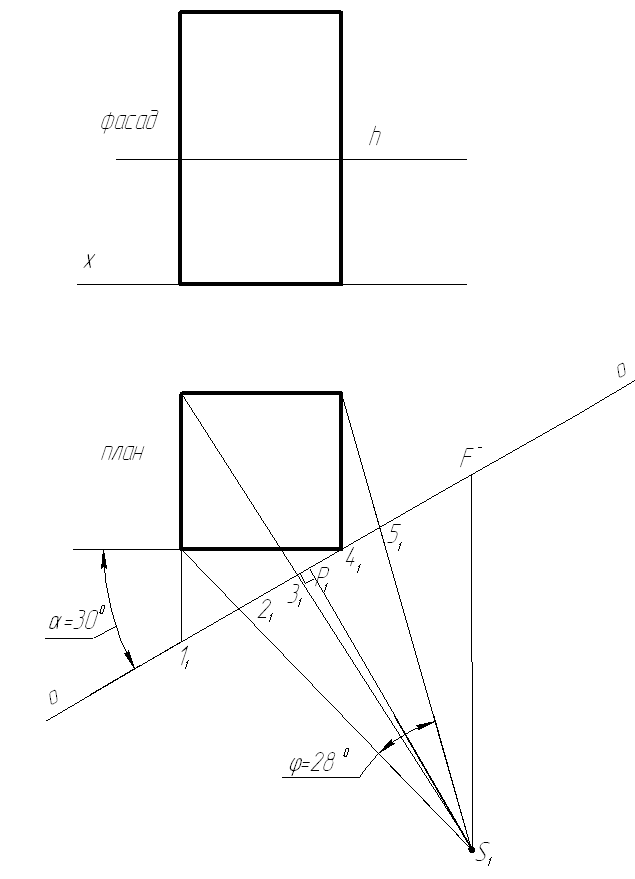
Рисунок 3.5.3 – Подготовительный этап построения перспективы способом архитекторов с одной точкой схода
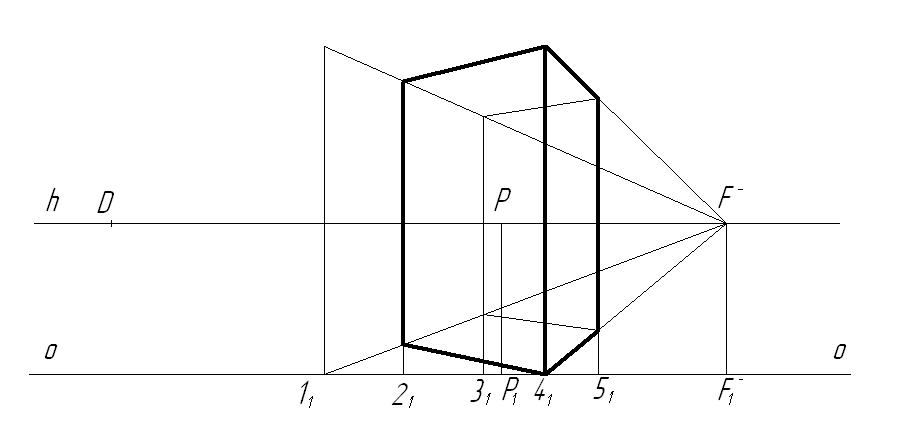 Рисунок
3.5.4 - Построение перспективы способом
архитекторов с одной точкой схода
Рисунок
3.5.4 - Построение перспективы способом
архитекторов с одной точкой схода
