1.3.2.5 Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. Так, прямая l параллельна прямой b, расположенной в плоскости  в соответствии с рисунком 1.3.20, следовательно,

l|| (прямая l параллельна плоскости ).

На комплексном чертеже это условие обеспечивается параллельностью соответствующих проекций прямой l и прямой b в соответствии с рисунком 1.3.21. Так, l₁||b₁ и l₂||b₂, следовательно, l||.

Рисунок 1.3.20 – Параллельность прямой и плоскости

Рисунок 1.3.21 – Комплексный чертёж параллельных прямой и плоскости

1.3.2.6 Параллельность плоскостей

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Так, пересекающиеся прямые с и d плоскости  (рисунок 1.3.22 а) параллельны пересекающимся прямым с’ и d’ плоскости , следовательно, плоскость  параллельна плоскости  (||).

Рисунок 1.3.22 – Параллельность плоскостей

На комплексном чертеже это условие обеспечивается параллельностью соответствующих проекций прямых с и d плоскости  и прямых с и d плоскости . Так, с||с’ и d||d’, следовательно, || в соответствии с рисунком 1.3.22 б.

1.3.2.7 Перпендикулярность прямой и плоскости

Из элементарной геометрии известно, что прямая f₂, перпендикулярна плоскости, если она перпендикулярна двум прямым, лежащим в этой плоскости.

На заданной плоскости в качестве двух пересекающихся прямых удобно выбирать линии уровня – горизонталь или фронталь. В этом случае можно воспользоваться свойствами проекций прямого угла.

Теорема. Для того, чтобы прямая была перпендикулярна плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Задача. Построить проекции перпендикуляра l, опущенного из точки D(D₁,D₂) на плоскость общего положения Σ(АВС) (рисунок 1.3.23).

Решение:

1. В плоскости Σ(АВС) проведем горизонталь h(h₁,h₂) и фронталь f(f₁,f₂).

2. Выполним условия перпендикулярности прямой и плоскости. Для этого из точки D₁ проведем горизонтальную проекцию перпендикуляра l₁ таким образом, чтобы l_1┴ h₁, а из точки D₂ проведем l₂, чтобы l₂ f₂.

3) Прямая l в этом случае перпендикулярна плоскости Σ(АВС), так как она перпендикулярна двум пересекающим прямым этой плоскости (h∩f). Таким образом l₁ h₁ и l₂ f₂ , следовательно l Σ(АВС).

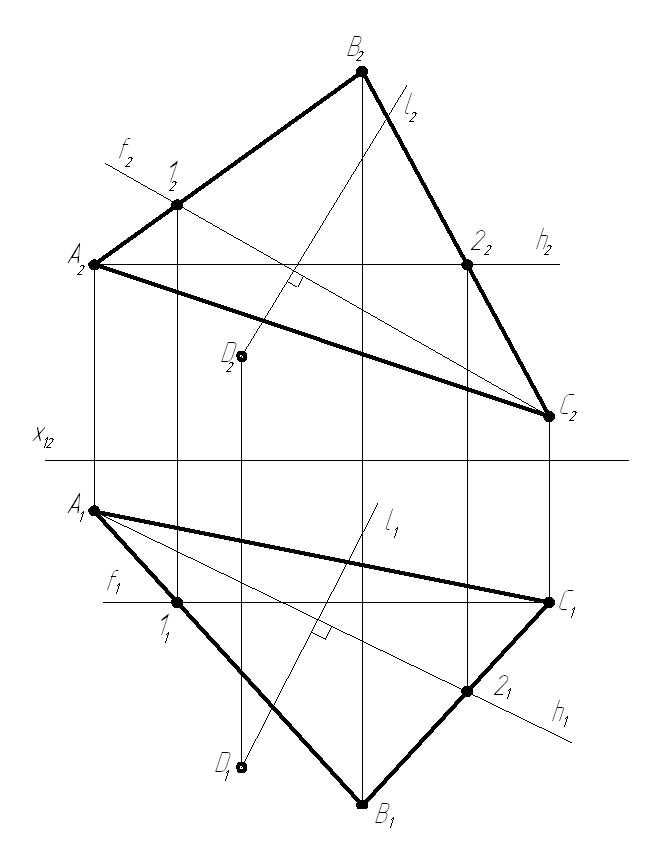
Рисунок 1.3.23 – Перпендикулярность прямой и плоскости

1.3.2.8 Пересечение прямой линии с плоскостью

Это есть позиционная задача, т.к. в ней определяется общий элемент данных геометрических объектов, т.е. их точка пересечения, что соответствует рисунку 1.3.24.

Алгоритм решения задачи основывается на следующем способе:

1) через прямую линию проводят вспомогательную проецирующую плоскость-посредник;

2) находят линию пересечения вспомогательной плоскости с данной

плоскостью;

3) отмечают точку пересечения полученной линии с данной прямой;

4) определяют видимость прямой относительно даной плоскости.

Через прямую а, которая пересекает плоскость общего положения, заданная треугольником АВС, в соответствии с рисунком 1.3.24 проведена вспомогательная фронтально проецирующая плоскость (₂), обозначенная на чертеже ₂а₂.

Линией пересечения b плоскости  с заданной плоскостью треугольника АВС является прямая линия. Эта линия строится с помощью точек 1 и 2. Первоначально отмечаем фронтальные проекции 1₂ и 2₂ этих точек в пересечении следа ₂ плоскости с фронтальными проекциями А₂В₂ и А₂С₂ соответствующих сторон треугольника АВС. Затем по свойству принадлежности определяем горизонтальные проекции точек 1 и 2 на горизонтальных проекциях этих сторон.

Пересечение линии b₁ c линией a₁ определяет горизонтальную проекцию К₁ искомой точки К. Фронтальная проекция К₂ точки К получается в пересечении линии связи, проведённой из точки К₁ с линией a_2.

Видимость прямой а относительно плоскости треугольника АВС определена с помощью конкурирующих точек 1, 1 и 3, 3.

Рисунок 1.3.24 – Пересечение прямой линии с плоскостью