
- •Высшая математика
- •Контрольные задания
- •Предисловие
- •Рекомендации по выполнению и оформлению контрольных работ
- •Контрольные задания
- •Элементы векторной алгебры и аналитической геометрии
- •2. Элементы линейной алгебры
- •3. Введение в математический анализ
- •Производная и ее приложения
- •5. Приложения дифференциального исчисления
- •Дифференциальное исчисление функций нескольких переменных
- •7. Неопределенный и определенный интегралы
- •8. Кратные, криволинейные и поверхностные интегралы. Векторный анализ
- •9. Дифференциальные уравнения
- •10. Ряды
- •11. Теория вероятностей и математическая статистика
- •II. Задачи 1-5
- •12. Элементы математического программирования
- •Программы по математике
- •1. Элементы линейной алгебры
- •2. Элементы векторной алгебры
- •3. Элементы аналитической геометрии на плоскости и в пространстве
- •4. Комплексные числа. Многочлены
- •6. Введение в математический анализ
- •Дифференциальное исчисление функций
- •8. Исследование функции с помощью производных
- •9. Функции нескольких переменных
- •10. Неопределенный интеграл
- •13. Дифференциальные уравнения
- •20. Элементы математической статистики
- •26. Экономико – математические модели
- •Список литературы
- •Высшая математика Программы Контрольные задания
- •450078, Г. Уфа, ул. Чернышевского, 145, каб. 227; 78-69-85
II. Задачи 1-5
Задача 1. В каждой из трех урн содержится С черных и B белых шаров. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.
Задача 2. Имеется три партии деталей по (10+A+B+C) деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно (10+A), (10+B), (10+C). Из наудачу взятой партии наудачу извлечена деталь, оказавшаяся стандартной. Затем из той же партии вторично наудачу извлекли деталь, также оказавшуюся стандартной. И, наконец, из той же партии в третий раз наудачу извлекли деталь, которая также оказалась стандартной. Найти вероятность того, что детали были извлечены из второй партии.
Задача 3. Случайная величина X задана функцией распределения F(x)
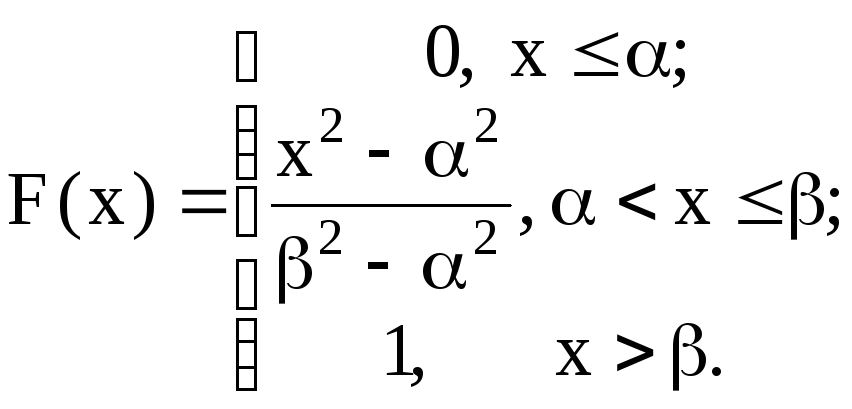
Требуется:
а) найти плотность распределения вероятностей;
б) построить графики интегральной и дифференциальной функций;
в) найти математическое ожидание и дисперсию случайной величины X;
г) определить вероятность того, что X примет значение, заключенное в интервале (a;b).
Правило составления исходных данных по шифру студента заочника. Считаем, что A,B,C составляют три последние цифры шифра (отметим, что если какая-то цифра шифра равна 0, то соответствующее ей значение A,B или C принимается равным 10).
Для задачи 3 необходимые параметры вычисляем по формулам:
![]()
Задача 4. Дано статистическое распределение выборки
|
|
|
|
|
|
|
|
|
|
|
3 |
7 |
15 |
17+B+C |
40-B-C |
13 |
5 |
где
hx
= 0,7C;
![]()
Требуется:
1. Найти методом произведений выборочные: среднюю, дисперсию и среднее квадратическое отклонение, асимметрию и эксцесс.
2. Построить нормальную кривую.
3.
Найти доверительный интервал для оценки
неизвестного математического ожидания
M(X), полагая что X имеет нормальное
распределение, среднее квадратическое
отклонение
![]() и
доверительная вероятность
и
доверительная вероятность
![]() .
.
Задача 5.
Найти:
1) выборочное уравнение прямой![]() регрессии Y на X;
регрессии Y на X;
-
выборочное уравнение прямой
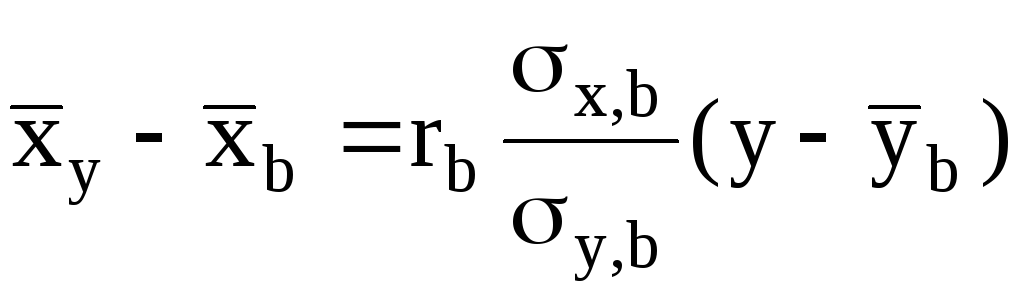
регрессии X на Y.
Построить диаграмму рассеивания и графики уравнений регрессии по данной корреляционной таблице:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
2 |
2 |
1 |
|
|
|
|
5 |
|
|
|
4 |
3 |
2 |
|
|
|
9 |
|
|
|
1 |
6 |
C+7 |
4 |
|
|
18+C |
|
|
|
|
5 |
B+4 |
23-B-C |
|
|
32-C |
|
|
|
|
|
4 |
7 |
6 |
|
17 |
|
|
|
|
|
|
5 |
4 |
|
9 |
|
|
|
|
|
|
1 |
2 |
3 |
6 |
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
3 |
7 |
15 |
17+B+C |
40-B-C |
13 |
5 |
|
где
hx
= 0,7C;
![]()
![]() =
2,2A+0,3C; hy
= 0,6B;
=
2,2A+0,3C; hy
= 0,6B;
![]() = y1 + (i-1)hy
,
= y1 + (i-1)hy
,
![]() .
.
