8. Кратные, криволинейные и поверхностные интегралы. Векторный анализ

261-270. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах

261. . 262. .

263. . 264. .

265. . 266. .

267. . 268. .

269. . 270. .

271-280. Вычислить с помощью тройного интеграла объём тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость ХОY.

271. .

272.

273. .

274. .

275. .

276. .

277. .

278.

279.

280.

281. Вычислить криволинейный интеграл вдоль дуги окружности , , обходя её против хода часовой стрелки от точки до точки . Сделать чертеж.

282. Вычислить криволинейный интеграл вдоль ломанной где . Сделать чертёж.

283. Вычислить криволинейный интеграл вдоль границы треугольника , обходя её против хода часовой стрелки, если Сделать чертёж.

284. Вычислить криволинейный интеграл вдоль дуги параболы от точки до точки . Сделать чертеж.

285. Вычислить криволинейный интеграл вдоль верхней половины эллипса . Сделать чертеж.

286. Вычислить криволинейный интеграл вдоль ломаной где . Сделать чертеж.

287. Вычислить криволинейный интеграл вдоль дуги кривой от точки до точки . Сделать чертёж.

288. Вычислить криволинейный интеграл вдоль отрезка прямой от точки до точки . Сделать чертёж.

289. Вычислить криволинейный интеграл вдоль дуги параболы от точки до точки . Сделать чертёж.

290. Вычислить криволинейный интеграл вдоль дуги кривой от точки до точки . Сделать чертёж.

291-300. Даны векторное поле и плоскость Ax + By + Cz + D = 0(p), которая совместно с координатными плоскостями образует пирамиду V. Пусть - основание пирамиды, принадлежащее плоскости (p); -контур, ограничивающий ; -нормаль к , направленная вне пирамиды V. Требуется вычислить:

1. поток векторного поля через поверхность в направлении нормали ;

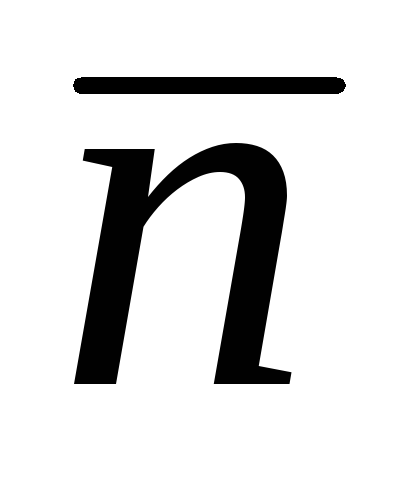2. циркуляцию векторного поля по замкнутому контуру непосредственно и применив теорему Стокса к контуру и ограниченной им поверхности с нормалью .

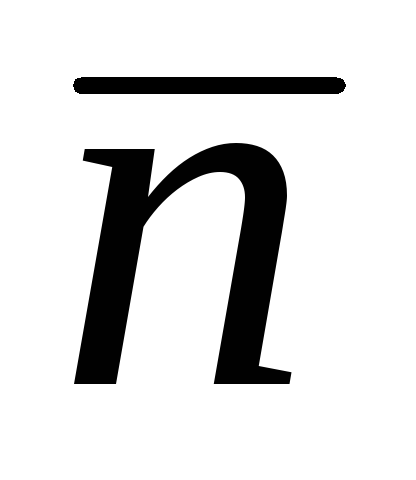3. поток векторного поля через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности непосредственно, применив теорему Остроградского. Сделать чертеж.

291.

292.

293.

294.

295.

296.

297.

298.

299.

300.

9. Дифференциальные уравнения

301-310. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию при .

301. .

302. .

303. .

304. .

305. .

306. .

307. .

308. .

309. .

310. .

311-330. Найти общее решение дифференциального уравнения

311. . 312. .

313. . 314. .

315. . 316. .

317. . 318. .

319. . 320. .

321. . 322. .

323. . 324. .

325. . 326. .

327. . 328. .

329. . 330. .

331-340. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям при .

331. .

332. .

333. .

334. .

335. .

336. .

337. .

338. .

339. .

340. .

341-350. Найти частное решение дифференциального уравнения,

удовлетворяющее начальным условиям .

341.

342.

343.

344.

345.

346.

347.

348.

349.

350.