5. Приложения дифференциального исчисления

131-150. Исследовать методами дифференциального исчисления функцию у = f(x) и, используя результаты исследования, построить ее график.

131. 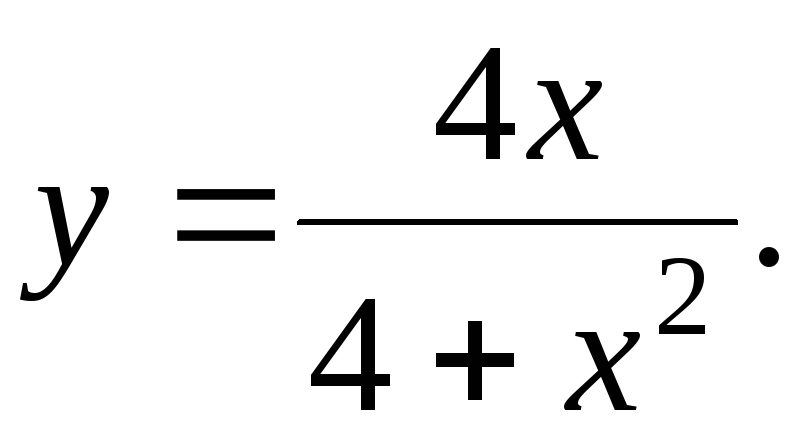132. у = 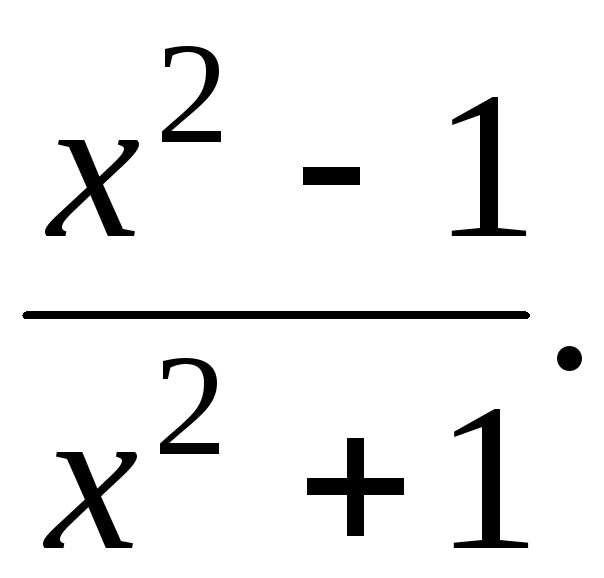133. у =

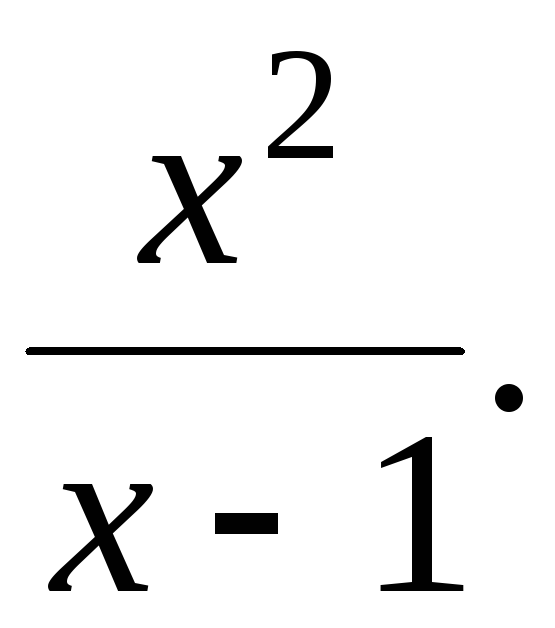134. у = 135. у =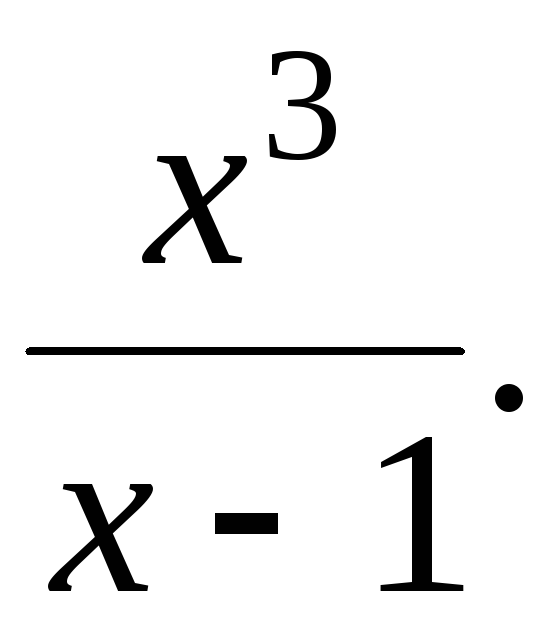 136.

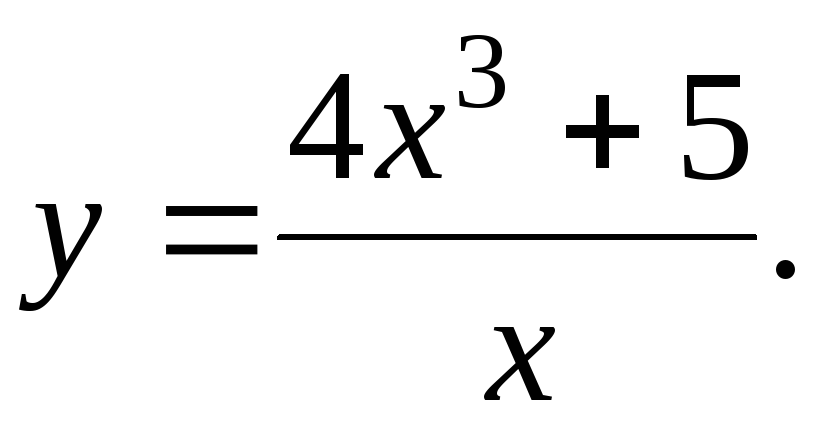
13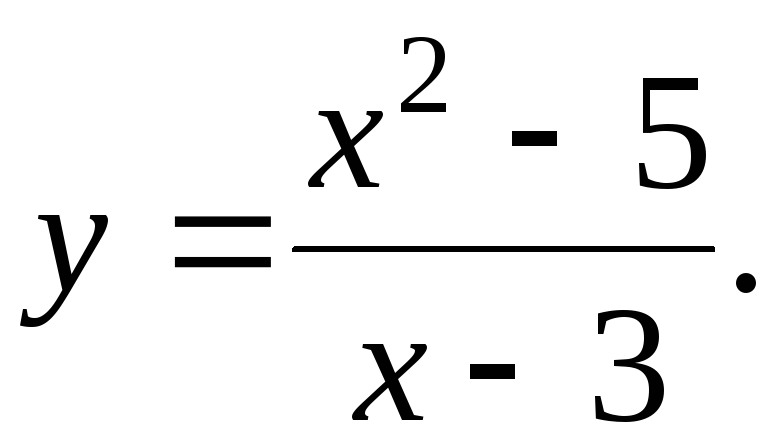7. 138.

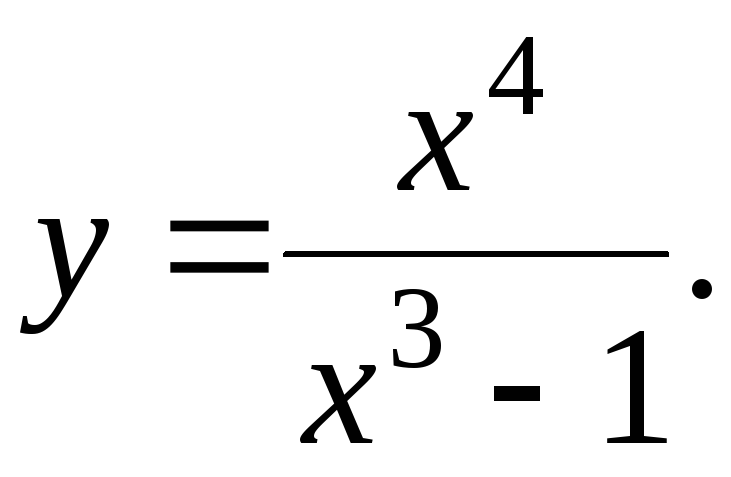
139. 140.

141.

142.

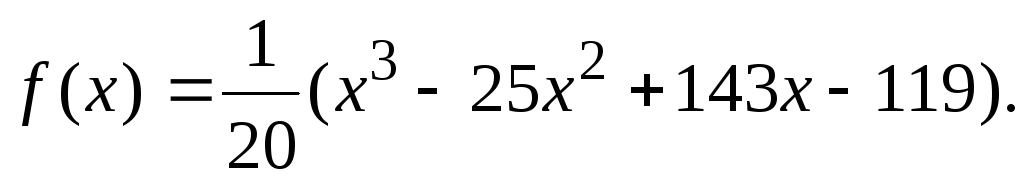
143.

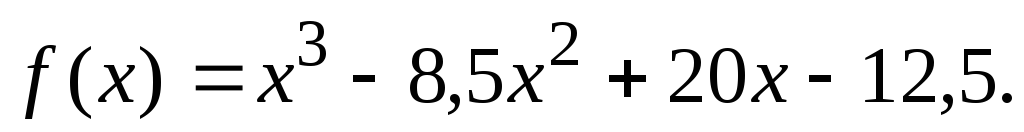
144.

145.

146.

147.

148.

149.

150.

6. Дифференциальное исчисление функций нескольких переменных

151-160. Дана функция z = f(x;y). Показать, что

151.

152.

153. .

154.

155.

156.

157.

158.

159.

160.

161-170. Дана функция и две точки и . Требуется: 1) вычислить значение в точке В; 2) вычислить приближенное значение функции в точке В, исходя из значения функции в точке А и,

заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом; 4) составить уравнение касательной плоскости к поверхности в точке .

161.

162.

163.

164.

165.

166.

167.

168.

169.

170.

171-180. Найти наименьшее и наибольшее значения функции

z = f (x ; y) в замкнутой области Д, заданной системой неравенств. Сделать чертеж.

171. .

172. .

173. .

174. .

175. .

176.

177.

178. .

179. .

180. .

181-190. Даны функция , точка и вектор .

Найти: 1) в точке А; 2) производную в точке А по направлению вектора .

181. .

182. .

183. .

184. .

185. .

186. .

187. .

188. .

189. .

190. .

191-200. Экспериментально получены пять значений функции при пяти значениях аргумента, которые записаны в таблице:

	1	2	3	4	5

Методом наименьших квадратов найти функцию вида , выражающую приближенно (аппроксимирующую) функцию . Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции .

191. .

192. .

193. .

194. .

195. .

196. .

197. .

198. .

199. .

200. .

201-210. Найти полный дифференциал функции z = f (x ;y) .

201. .

202. .

203. .

204. .

205. .

206. .

207. .

208. .

209. .

210. .

7. Неопределенный и определенный интегралы

211-230. Найти неопределенные интегралы. Результаты проверить дифференцированием.

211.

212.

213.

214.

215.

216.

217.

218.

219.

220.

221.

222.

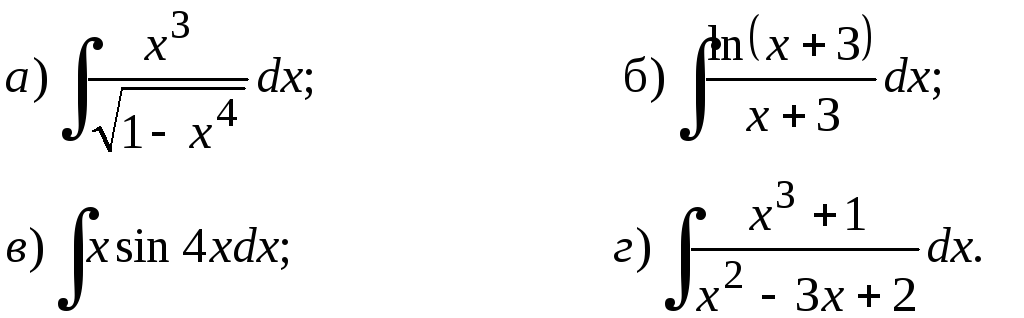
223.

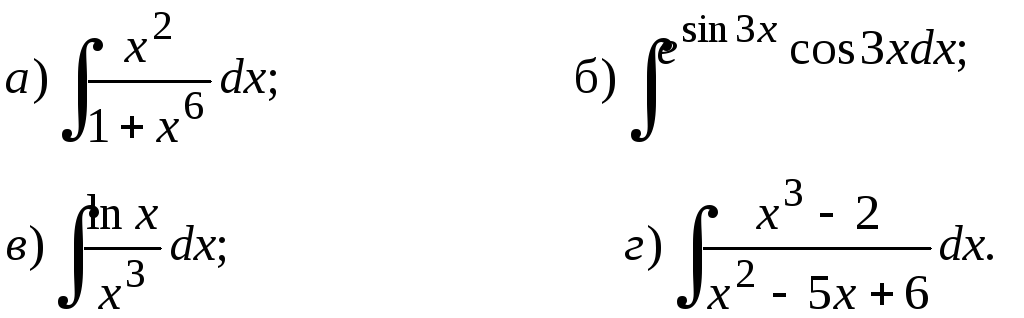
224.

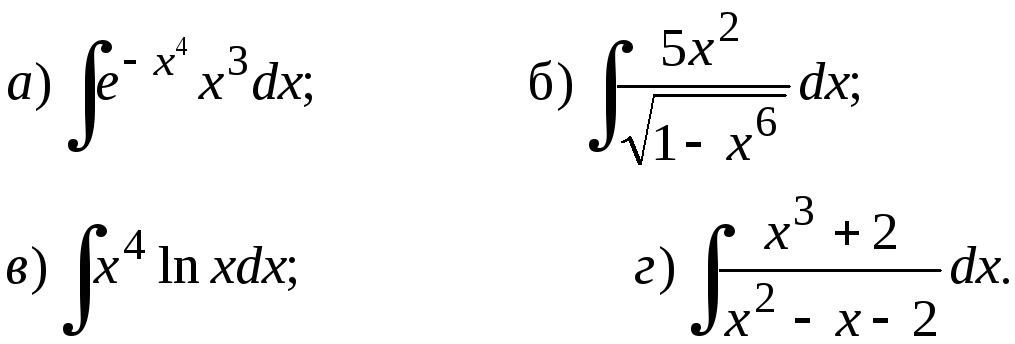
225.

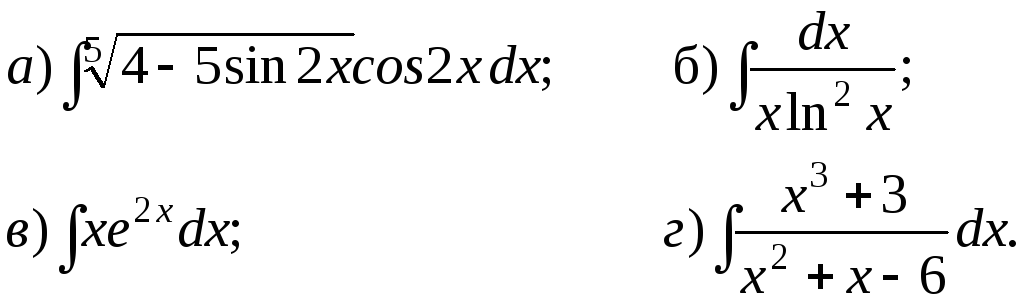
226.

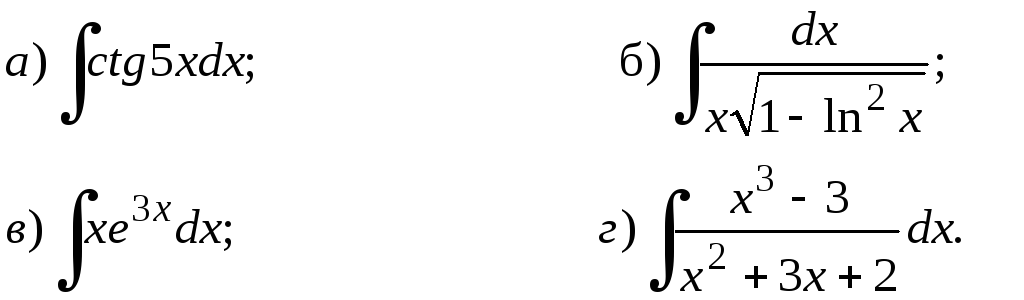
227.

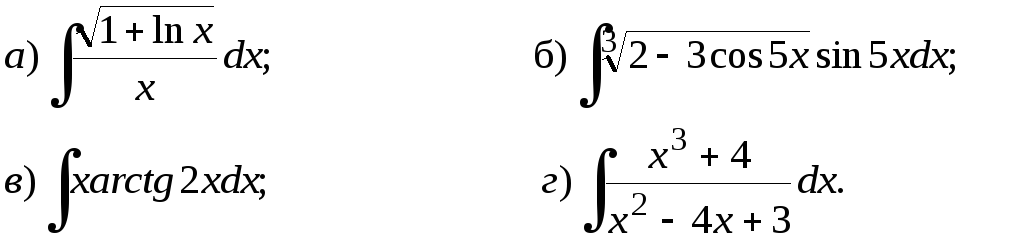
228.

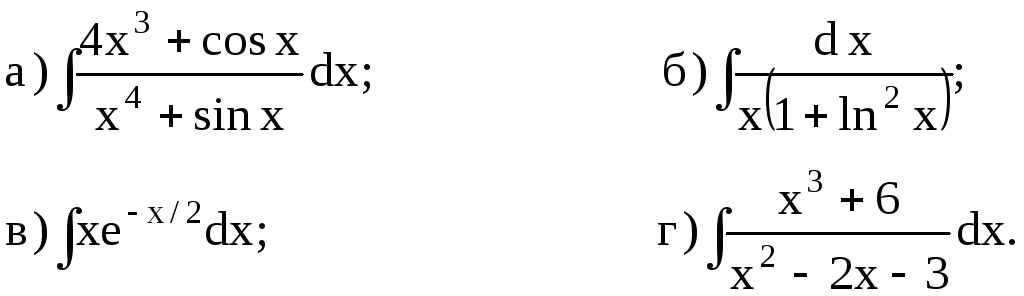
229.

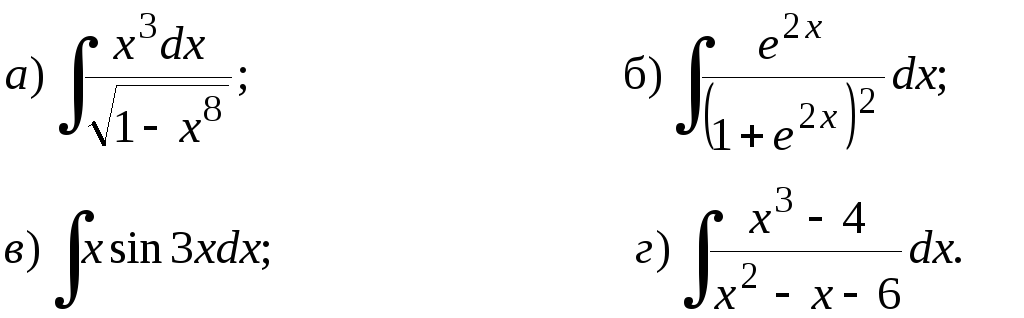
230.

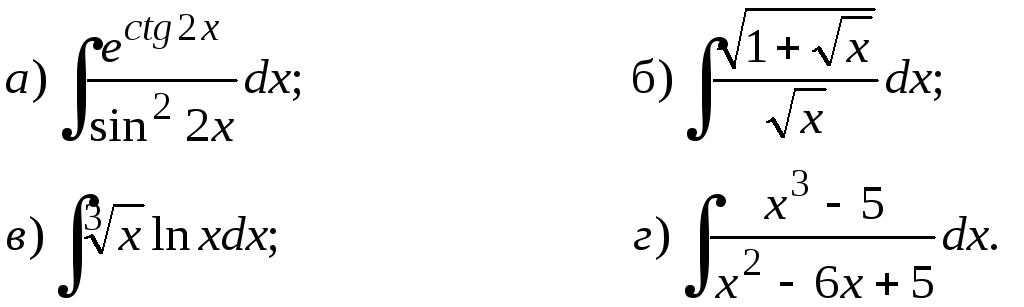
231-240. Вычислить по формуле Ньютона-Лейбница определенный интеграл .

231.

.

241-250. Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.

241. .

242. .

243. .

244. .

245. .

246. .

247. .

248. .

249. .

250. .

251. Вычислить площадь фигуры, ограниченной параболой и прямой .

252. Вычислить площадь фигуры, ограниченной одной аркой циклоиды и осью Ох.

253. Вычислить площадь фигуры, ограниченной кардиоидой

254. Вычислить площадь фигуры, ограниченной четырехлепестковой розой .

255. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами .

256. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом , параболой и осью Оу.

257. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми .

258. Вычислить длину полукубической параболы от точки А(2;0) до точки В(6;8).

259. Вычислить длину кардиоиды .

260. Вычислить длину одной арки циклоиды .
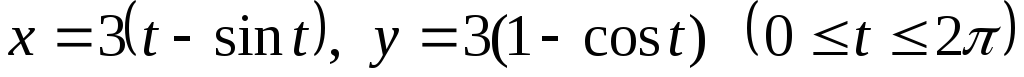