4.2.Нечеткость и приближенные функциональные зависимости.
Используя подходящие подходящие определения элементов и транзакций НАП могут описать структуру паттерна отличную от описанной в предыдущей секции. В дальнейшем мы суммируем методологию обработки функциональных зависимостей в реляционных базах данных при помощи ассоциативных правил с подходящим представлением элементов и транзакций.
Пусть
RE
множество атрибутов и r
экземпляр RE.
Функциональная зависимость
,
содержится в r,
если значение
определяет
для каждого кортежа
.
Формально эту зависимость можно описать
можно описать так
,
if
then
Зависимость содержится в RE , если она содержится во всех экземплярах RE.
Открытие скрытых знаний это очень интересно, но в тоже время очень трудно найти «превосходную» зависимость, преимущественно потому, что обычно существуют исключения. Для того чтобы справиться с этим существует два основных подхода (оба представляют собой некий вид сглаженных зависимостей): нечеткие функциональные зависимости и аппроксимация зависимостей.
Мы
используем АП, чтобы представить
приближенные зависимости. Для этой цели
ассоциируем транзакции и элементы с
парами кортежи и атрибуты соответственно.
Договоримся, что элемент ассоциирован
с атрибутом X,
,
и транзакция
ассоциированная с парными кортежами
,
где
.
Множество транзакций, соотнесенное на
экземпляр r
в RE
обозначим как
,
содержащее
транзакций.
Очевидно,
что поддержка и достоверный фактор АП
в
измеряют
важность и точность соответствующей
приближенной функциональной зависимости.
Главный недостаток этого пути
вычислительная сложность, потому что
и
алгоритм имеет линейную сложность от
числа транзакций. Мы решили эту проблему
путем анализа нескольких транзакций в
то время. Алгоритм хранит поддержку для
каждого элемента формы
с
для
того, чтобы получить поддержку
.
Пример
4. Пусть
отношение
на таблице 7. Экземпляр
RE={ID,
Y ear, Course, Lastname}.
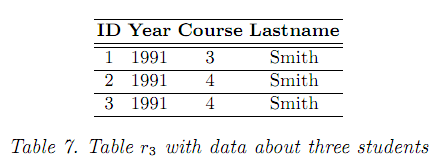
Таблица
8 показывает T
множество
и таблица 9 содержит некоторые АП из
.
Точность и поддержка АП в таблице 9 измеряют точность и поддержку соответствующей функциональной зависимости.
Нечеткие
ассоциативные правила необходимы и в
этом контексте, когда участвуют
количественные признаки. Наши алгоритмы
обеспечивают
не только приближенная зависимость, но
и модель, которая состоит из набора АП
(в обычном смысле в реляционных базах
данных), касающихся значений предшествующих
со значениями последующих зависимостей.
Но когда атрибуты количественные, эта
модель страдает теми же проблемами, что
и в предыдущей подсекции. Чтобы справиться
с ними, мы предлагаем использовать
множество лингвистических меток. Набор
меток
индуцирует
нечеткое схожее отношение
в
области X
следующим образом.
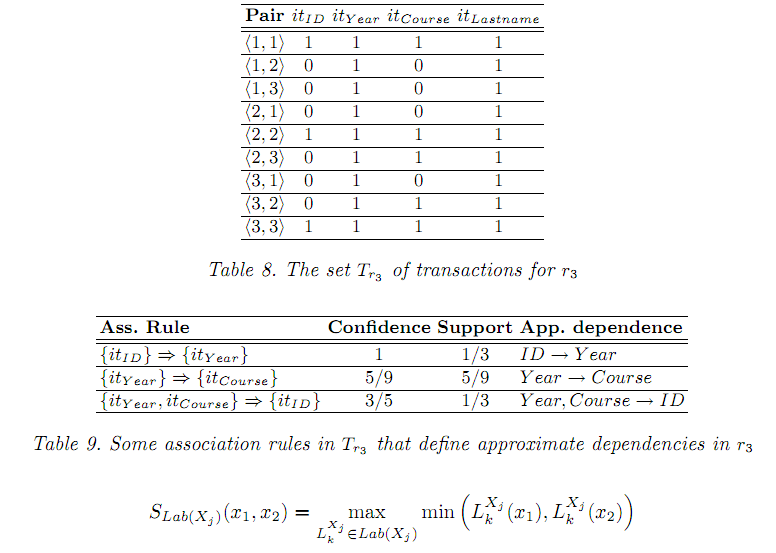
Для
всех
,
принимая, что для каждого
есть один
,
такой что
Тогда
элемент
в транзакции
со степенью
.
Транзакции из таблицы r
нечеткие
и обозначим как
.
В новой ситуации мы можем найти
приближенную зависимость в r
ища нечеткие ассоциативные правила
(НАП) в
.Моделью
таких приближенных зависимостей будет
множество ассоциативных правил из
.
Эти зависимости могут быть использованы
для обобщения данных в отношение.
Функциональные зависимости могут быть сглажены (скорее всего, имелось в виду вместо «сглажены» - «представлены как» {мое личное мнение}) в нечеткие функциональные зависимости несколькими альтернативными способами представленными в [16]. Мы показали, что большинство из них можно получить, заменяя равенство и универсальный квантификатор в правиле 5, используя отношение подобия S и нечеткий квантификатор Q соответственно[34].
Для
примера, пусть
отношение сходства[25] и
такое что,
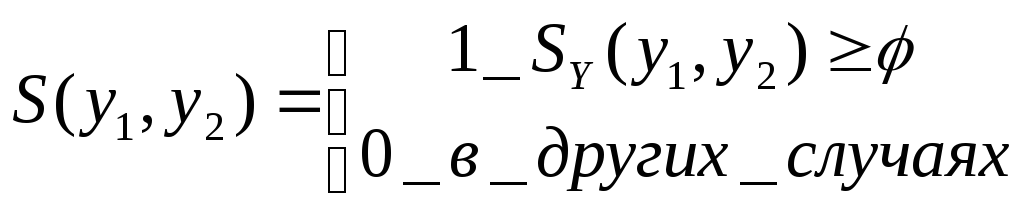
Так
же пусть
,
где
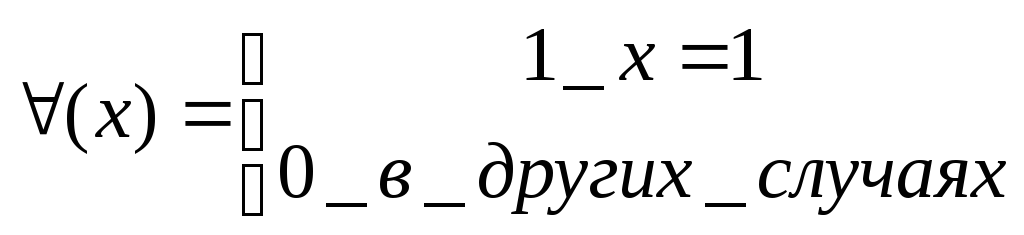
Функциональная
зависимость
определяется как [26]
,
if
then
Может
быть смоделирована в r
,
используя ассоциативные правила из
.
Здесь
обозначает нечеткое множество нечетких
сходств, заданными S
между
парами
кортежей из r.
Мы также столкнулись с более общей задачей: интеграции нечетких и приближенных зависимостей в то, что мы называем нечеткие количественные зависимости [34] (то есть нечеткие функциональные зависимости с исключениями). Заметим, что наш семантический подход, основанный на оценке количественного предложения позволяет оценить правила более гибким путем. Следовательно, иметь дело с определенными видами паттернов возможно, как мы увидели выше.