
- •2. Поиск ап(Ассоциативные правила)
- •2.1 Формальная модель.
- •Определение модели вычисления точности и важности.
- •2.3 Алгоритмы выявления ассоциативных правил.
- •2.4 Ассоциативные правила в реляционной базе данных.
- •Нечеткие транзакции и нечеткие ассоциативные правила.
- •3.2. Нечеткие транзакции и нечеткие ассоциативные правила. Наш путь
- •Поддержка и доверие в нечетких ассоциативных правилах.
- •Различные модели для определения точности и важности.
- •4 Приложение.
- •Нечеткие ассоциативные правила в реляционной базе данных.
- •4.2.Нечеткость и приближенные функциональные зависимости.
- •Связанные правила
-
Нечеткие транзакции и нечеткие ассоциативные правила.
Интеллектуальная обработка данных в общем и выявление ассоциативных правил особенно являются молодыми темами, но число статей посвященных данной тематике довольно большое и во многих статьях рассматривается интеллектуальная обработка АП, содержащих количественные атрибуты в реляционной базе данных используя нечеткие множество и лингвистические переменные, чтобы уменьшить неравномерность (глубину детализации) и перевести проблему в более естественный и понимаемый вид.
3.2. Нечеткие транзакции и нечеткие ассоциативные правила. Наш путь
Определение
5. Нечеткая
транзакция - это непустое нечеткое
подмножество
![]()
Для
каждого
![]() отметим
отметим
![]() степень
принадлежности
степень
принадлежности
![]() в нечеткой транзакции
в нечеткой транзакции
![]() .
Заметим, что
.
Заметим, что
![]() степень включения множества элементов
степень включения множества элементов
![]() ,
определим его как
,
определим его как
![]() .
.
Согласно
определению 5, транзакция является
частным случаем нечеткой транзакции.
Мы представим множество нечетких
транзакций как посредством таблицы.
Колонки и строки обозначаются
идентификаторами элементов и транзакций
соответственно. Ячейка для элемента
![]() и транзакции
и транзакции
![]() содержит значение, принадлежащее
отрезку [0;1]. Степень принадлежности для
содержит значение, принадлежащее
отрезку [0;1]. Степень принадлежности для
![]() в
в
![]() имеет вид
имеет вид
![]() .
.
Пример
1. Пусть
![]() набор элементов. Таблица 2 демонстрирует
6 нечетких транзакций определенных в
набор элементов. Таблица 2 демонстрирует
6 нечетких транзакций определенных в
![]() .
Здесь
.
Здесь
![]() ,
,
![]() и так далее. В частности,
и так далее. В частности,
![]() жесткая (четкая) транзакция,
жесткая (четкая) транзакция,
![]() .
.
Пример
расчета степени включения
![]() ,
,
![]() ,
,![]()
Таблица 2.
|
|
|
|
|
|
|
|
0 |
0.6 |
0.7 |
0.9 |
|
|
0 |
1 |
0 |
1 |
|
|
1 |
0.5 |
0.75 |
1 |
|
|
1 |
0 |
0.1 |
1 |
|
|
0.5 |
1 |
0 |
1 |
|
|
1 |
0 |
0.75 |
1 |
Определение
6. Пусть
![]() множество элементов,
множество элементов,
![]() -
-
![]() множество и
множество и
![]() -
два четких подмножества, где
-
два четких подмножества, где
![]() и
и
![]() .
Ассоциативное правило
.
Ассоциативное правило
![]() содержится в
содержится в
![]() ,
если
,
если
![]() ,
,
То
есть степень включения для
![]() больше чем для
больше чем для![]() для каждой транзакции
для каждой транзакции
![]() .
Это определение сохраняет смысл
ассоциативного правила, потому как мы
принимаем
.
Это определение сохраняет смысл
ассоциативного правила, потому как мы
принимаем
![]() в некотором смысле, мы должны предполагать,
что
в некотором смысле, мы должны предполагать,
что
![]() дает, что
дает, что
![]() .
Поскольку транзакция является частным
случаем нечеткой транзакции, то
ассоциативное правило – частный случай
нечеткого АП.
.
Поскольку транзакция является частным
случаем нечеткой транзакции, то
ассоциативное правило – частный случай
нечеткого АП.
Заметим, что основной характерной чертой нашего подхода является моделирование нечетких транзакций с четкими элементами. Это достаточно обще, потому что в случае наличия актуальных нечеткие элементов: лейблы, нечеткие числа, и т.д. они будут производить предыдущую таблицу.
Поддержка и доверие в нечетких ассоциативных правилах.
Чтобы
оценить значения правила, мы используем
семантический путь, основанный на
эволюции количественных предложений.
Количественное предложение – это
выражение вида «![]() »,
где
»,
где
![]() и
и
![]() нечеткие
подмножества ограниченного множества
нечеткие
подмножества ограниченного множества
![]() и
и
![]() относительный (сравнительный) нечеткий
квантификатор. Сравнительный квантификатор
- это лингвистическая метка для нечеткого
процентного отношения, которое может
быть представлено в виде значений
нечеткого множества в диапазоне [0;1],
такие как «самый», «почти все», «многие».
относительный (сравнительный) нечеткий
квантификатор. Сравнительный квантификатор
- это лингвистическая метка для нечеткого
процентного отношения, которое может
быть представлено в виде значений
нечеткого множества в диапазоне [0;1],
такие как «самый», «почти все», «многие».
Семейство сравнительных квантификаторов, зовущихся связанными квантификаторами особенно важны для нас. Связанные квантификаторы, это те, которые удовлетворяют заданным свойствам:
-
 и
и
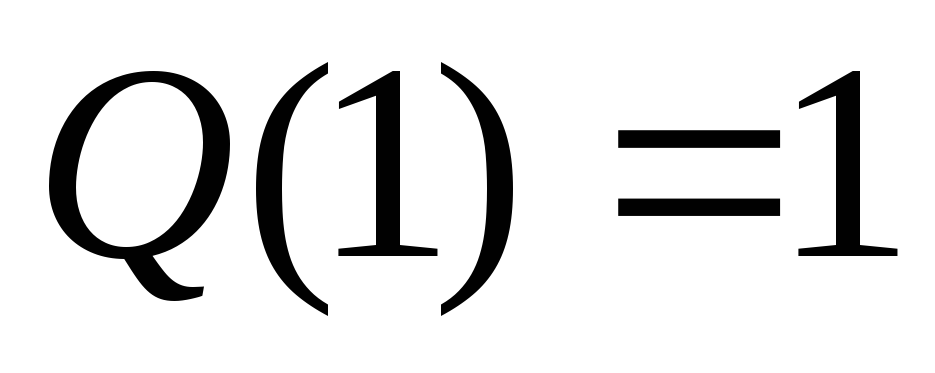
-
Если
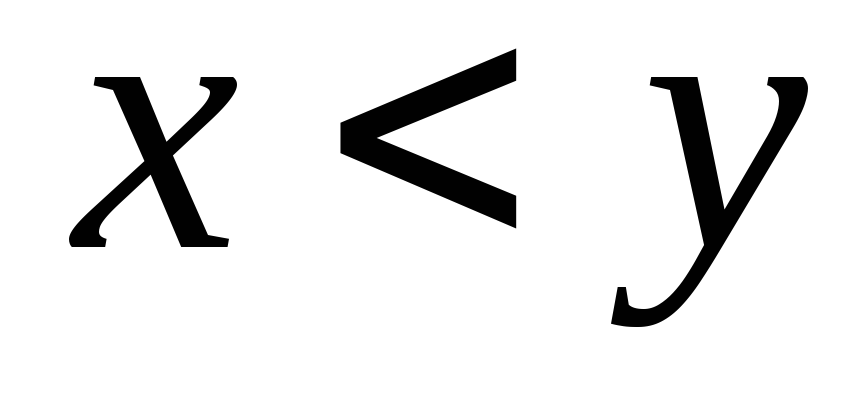 ,
тогда
,
тогда
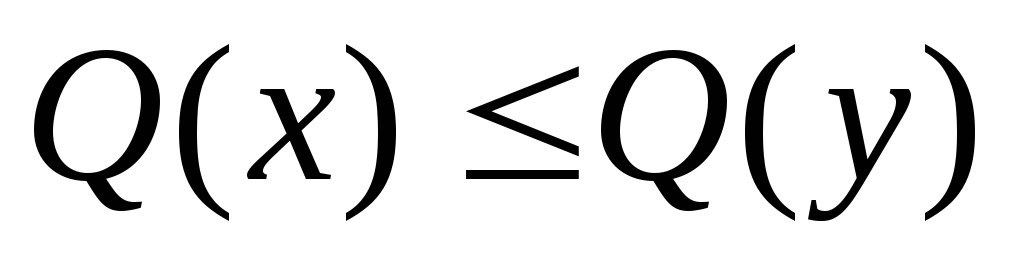
Например,
«многие молодые люди высокие», где
![]() =
«многие» и
=
«многие» и
![]() и
и
![]() возможные распределения порожденные
в множестве
возможные распределения порожденные
в множестве
![]() =
«люди» неточными термами «молодые» и
«высокие» соответственно. Частный
случай количественного предложения
открывается, когда
=
«люди» неточными термами «молодые» и
«высокие» соответственно. Частный
случай количественного предложения
открывается, когда
![]() ,
«многочисленные термы». Оценка
количественного предложения значением
[0;1] дает оценку степени выполнения
предложения.
,
«многочисленные термы». Оценка
количественного предложения значением
[0;1] дает оценку степени выполнения
предложения.
Определение
7. Пусть
![]() .
Поддержкой
.
Поддержкой
![]() в
в
![]() это оценка количественного предложения
это оценка количественного предложения
![]() ,
,
Где
![]() нечеткое
множество на
нечеткое
множество на
![]() определенное как
определенное как
![]()
Определение
8. Поддержкой
ассоциативного правила
![]() в множестве нечетких транзакций
в множестве нечетких транзакций
![]() это
это
![]() ,
т.е. оценка количественного предложения
,
т.е. оценка количественного предложения
![]()
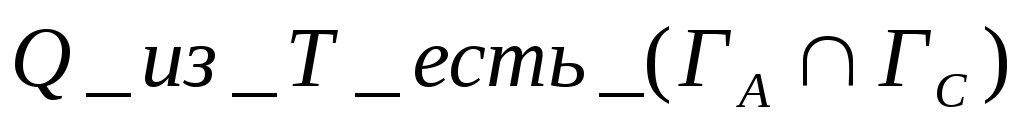
Определение
9. Доверием
нечеткого ассоциативного правила
![]() в множестве нечетких транзакций
в множестве нечетких транзакций
![]() - это оценка количественного предложения
- это оценка количественного предложения
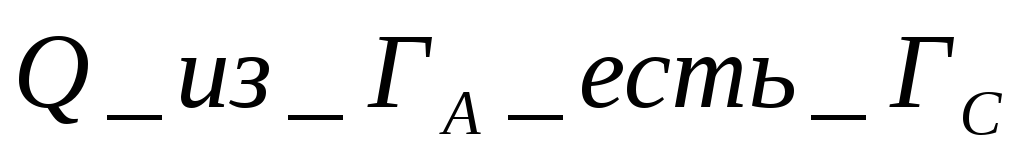
Заметим, что эти определения измерений поддержки и доверия, зависят от выбора метода оценки и квантификатор. Единственным ограничением по нашему мнению, являются следующие 4 интуитивно понятные свойства измерений для обычных ассоциативных правил:
-
Если
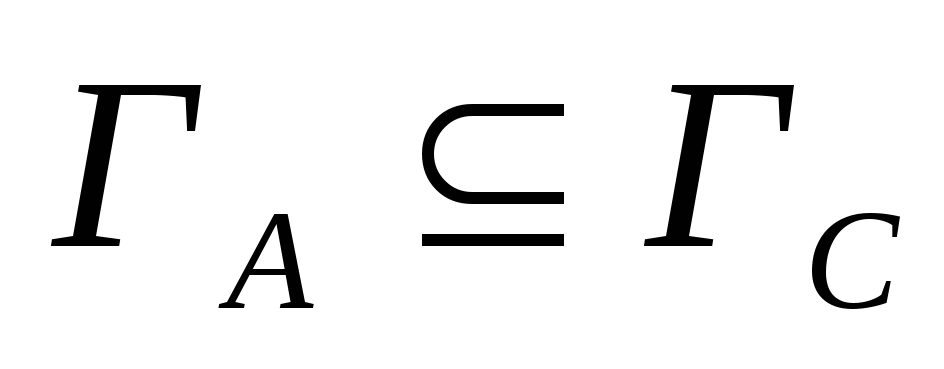 ,
то
,
то
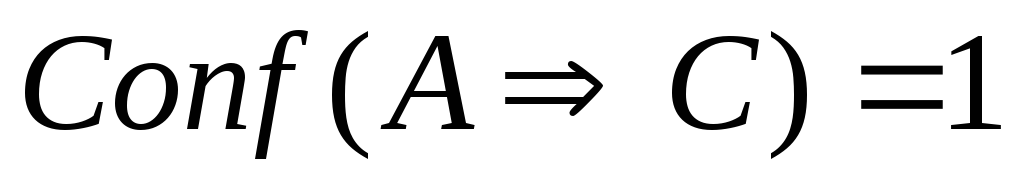
-
Если
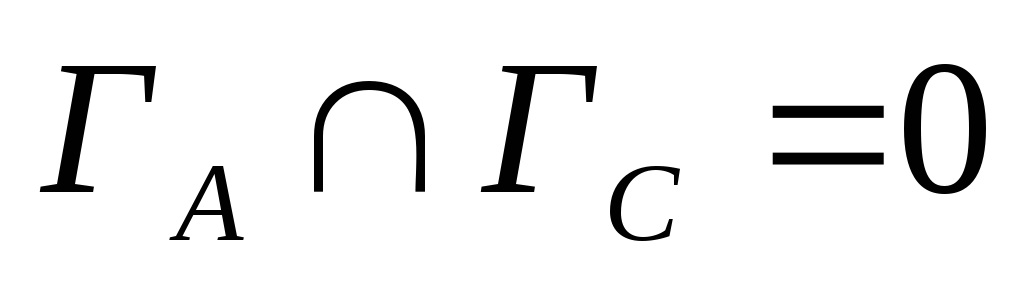 ,
тогда
,
тогда
 и
и
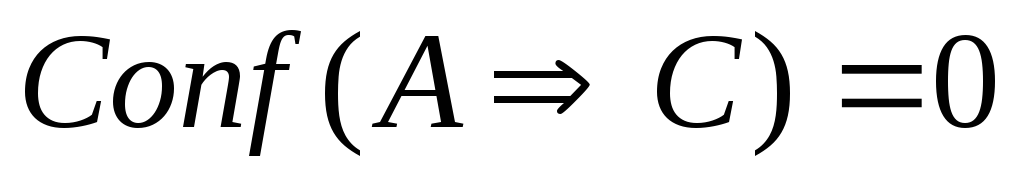
-
Если
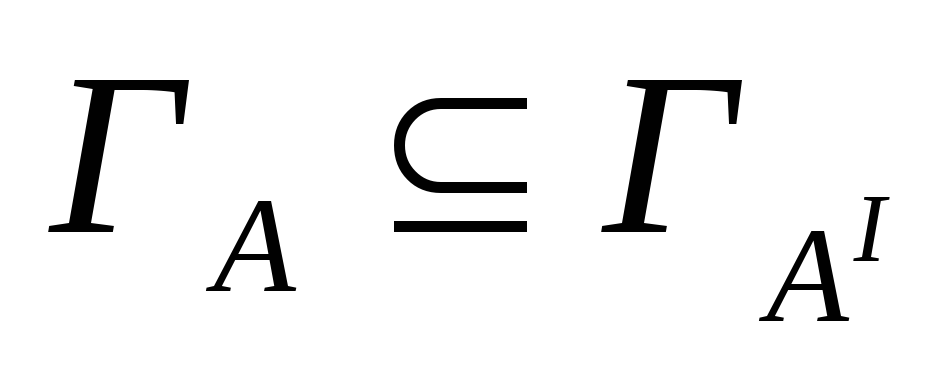 (в частности, когда
(в частности, когда
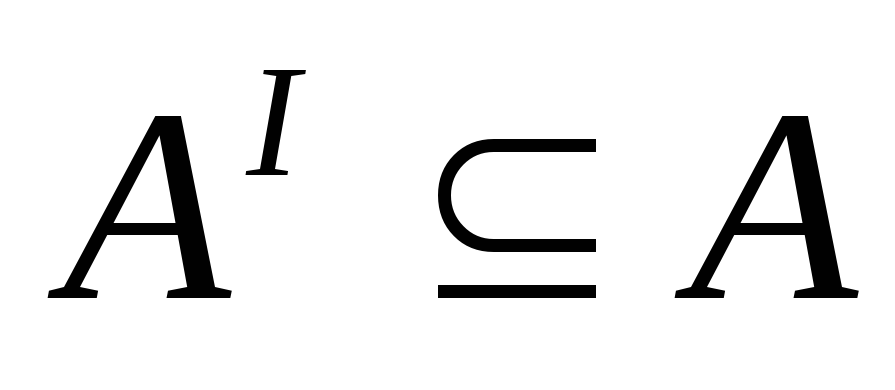 ),
тогда
),
тогда
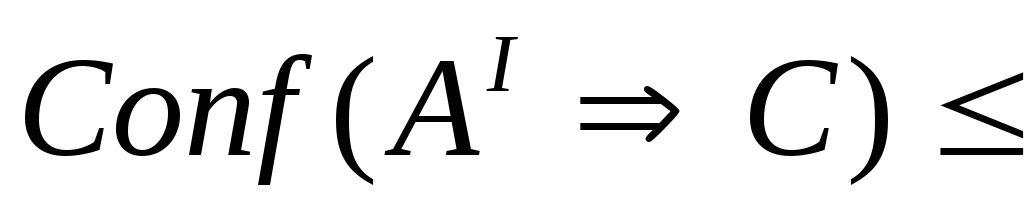
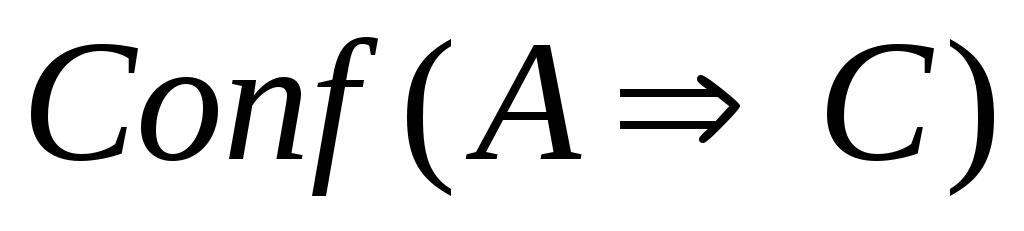
-
Если
 (в частности, когда
(в частности, когда
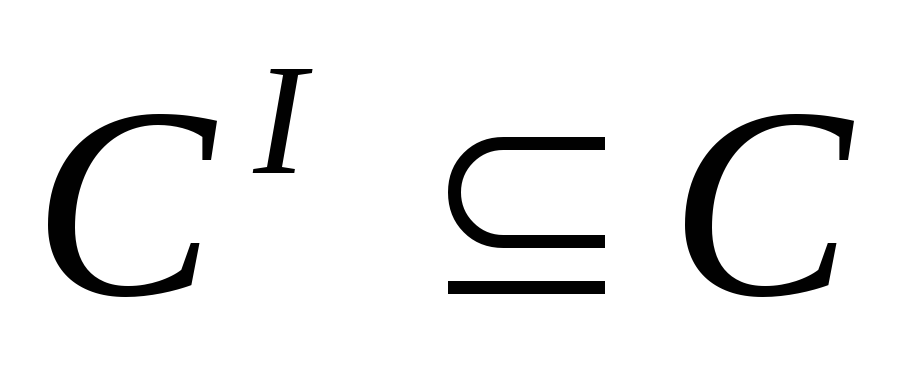 ),
тогда
),
тогда
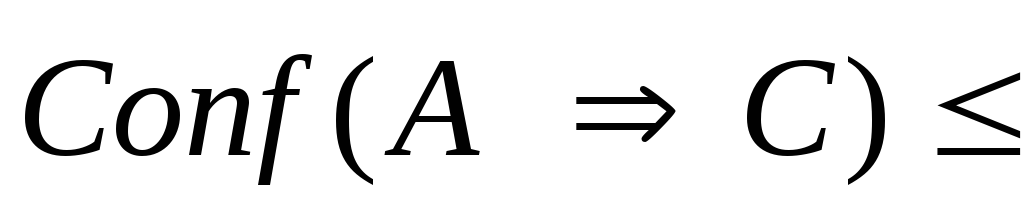
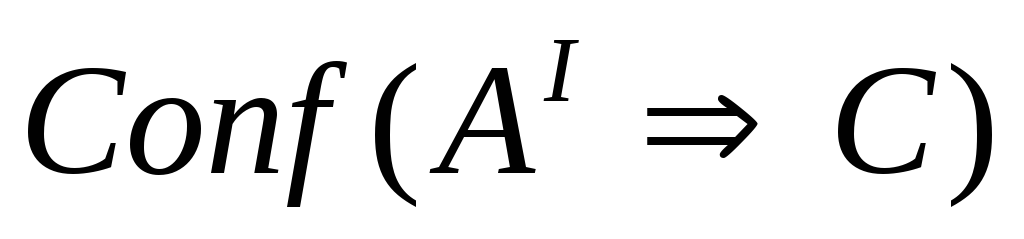
Мы
выбрали метод GD для вычисления предложения,
был показано как хорош он для проверки
свойства с более высокой производительностью
чем другие. Вычисление
![]() с помощью GD
с помощью GD
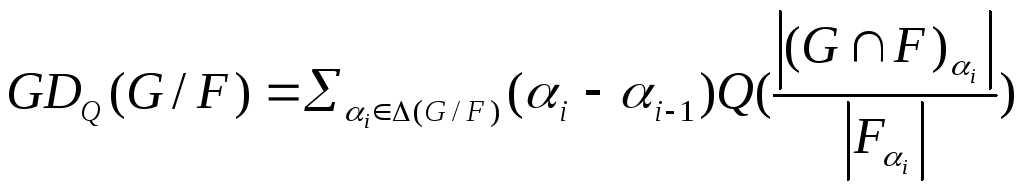
Где
![]() ,
,
![]() -
уровень множества
-
уровень множества
![]() и
и
![]() с
с
![]() для всех
для всех
![]() .
Множество
.
Множество
![]() предполагается нормированным. Если
нет, то
предполагается нормированным. Если
нет, то
![]() нормализуется и нормализирующий фактор
применяется к
нормализуется и нормализирующий фактор
применяется к
![]()
Оценка
квантификатора предложения
![]() с помощью метода GD
может быть интерпретировано как:
с помощью метода GD
может быть интерпретировано как:
- доказательство того, что процент объектов в F, которые также в G (относительно мощности G по отношению к F)
-
квантификатор-руководства агрегации
[52, 82] относительной мощности G по отношению
к F для каждого
![]() -срезом
одинаковым для обоих множеств.
-срезом
одинаковым для обоих множеств.
Таким
образом
![]() интерпретируется как свидетельство
(доказательство) того, что процент
транзакций в
интерпретируется как свидетельство
(доказательство) того, что процент
транзакций в
![]() есть Q.и
есть Q.и
![]() можно рассматривать как свидетельство
того, что процент транзакций в
можно рассматривать как свидетельство
того, что процент транзакций в
![]() ,
такой же и в
,
такой же и в
![]() есть Q.
В
обоих случаях, квантификатор – это
лингвистический параметр, который
определяет семантику измерений. Поскольку
свойства метода оценки GD,
легко показать, что любой связанный
квантификатор дает поддержку и доверие,
которые удовлетворяют 4 вышеупомянутым
свойствам.
есть Q.
В
обоих случаях, квантификатор – это
лингвистический параметр, который
определяет семантику измерений. Поскольку
свойства метода оценки GD,
легко показать, что любой связанный
квантификатор дает поддержку и доверие,
которые удовлетворяют 4 вышеупомянутым
свойствам.
С
другой стороны, мы предложили выбрать
квантификатор
![]() ,
определенный как
,
определенный как
![]() ,
поскольку он связанный и измерения
получаются на основании определений
7,8 и 9 являются обычными мерами в случае
четкого. Возможная интерпретация
значения мер четких ассоциативных
правил – есть доказательство того, что
поддержка (соответственно доверия)
правила есть
,
поскольку он связанный и измерения
получаются на основании определений
7,8 и 9 являются обычными мерами в случае
четкого. Возможная интерпретация
значения мер четких ассоциативных
правил – есть доказательство того, что
поддержка (соответственно доверия)
правила есть
![]() .
.
Позвольте нам в конце отметим, что выбор квантификатора позволяет нам изменять семантику значения в лингвистическим путем. Это гибкость очень полезна при использовании общей модели для тренировки различных типов паттернов, как мы увидим в секции приложения.
Пример 2. Согласно определению 7 поддержка некоторых элементов таблицы 2 в таблице 3.
Таблица
4 демонстрирует поддержку и доверие
нескольких нечетких АП в транзакции
![]() .
.
Заметим,
что
![]() поскольку
поскольку
![]()

