§ 5. Полярные уравнения эллипса, гиперболы и параболы Полярная система координат

Выберем на плоскости произвольную точку О, которую назовём полюсом, и проведём луч с началом в этой точке, который назовём полярной осью. Каждой точке плоскости поставим в соответствие упорядоченную пару чисел , где – расстояние от точки до полюса, а – угол между полярной осью и радиус-вектором точки (рис.3.14). Получим соответствие между множеством точек плоскости и множеством упорядоченных пар действитель- Рис. 3.14. ных чисел. Если , а или , то это соответствие будет взаимно однозначным на плоскости с выколотой точкой (полюсом).

Вывод полярных уравнений

Выберем одну из трёх кривых – эллипс, параболу или одну из ветвей гиперболы, и обозначим её . Полярную систему координат построим следующим образом: полюс поместим в фокус (для гиперболы берем фокус, соответствующий выбранной ветви), а полярную ось проведём перпендикулярно соответствующей этому фокусу директрисе в направлении от неё. Расстояние от фокуса до директрисы обозначим . Число называется фокальным параметром кривой. Тогда (рис. 3.15): , ;

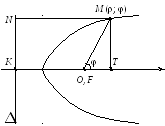
[Т§ 4] ,

откуда получаем уравнение

(1)

Это уравнение задаёт эллипс, параболу, левую ветвь гиперболы, когда полюс находится в левом фокусе, и правую ее ветвь, когда фокус находится в правом фокусе.

Если рассматриваемая кривая – эллипс, то , и из (1) видно,

Рис.3.15. что . Если рассматриваемая кривая – парабола, то и . В случае же, когда рассматривается одна из ветвей гиперболы, причём полюс находится в соответствующем фокусе, то для нахождения требуется решить неравенство , или , откуда находим . Таким образом, для одной из ветвей гиперболы

.

Это означает, что любой луч, выпущенный из фокуса эллипса, пересекает этот эллипс; единственный луч, выпущенный из фокуса параболы и не пересекающий её – это полярная ось; а лучи, выпущенные из фокуса гиперболы и не пересекающие соответствующую её ветвь, образуют целый угол.

Упражнение. Покажите, что в той же полярной системе уравнение противоположной ветви гиперболы выглядит так:

.

§ 6. Касательные к эллипсу, гиперболе, параболе

Во-первых, вспомним, что уравнение касательной к графику функции в точке выглядит так:

. (1)

Пусть задано некоторое уравнение

. (2)

Если существует единственное число такое, что , то говорят, что уравнение (2) на промежутке задаёт некоторую функцию . Такой способ задания функции называется неявным. Подробно теорию неявных функций вы будете изучать в курсе математического анализа. В частности, вам приведут обоснование следующего правила: для дифференцирования функции, заданной неявно, достаточно продифференцировать равенство, задающее эту функцию, считая переменную зависящей от переменной .

Составим уравнение касательной к гиперболе

. (3)

в принадлежащей ей точке . Уравнение (3) неявно задаёт две непрерывные функции: одну при , а вторую при . Для нахождения производной дифференцируем равенство (3):

,

откуда при находим

.

Тогда . Используя (1), запишем уравнение касательной к гиперболе (3) в точке :

.

Умножив это уравнение на и разделив его на , получим уравнение:

,

которое равносильно следующему:

.

В силу того, что точка принадлежит гиперболе (3), уравнение касательной приобретает конечный вид:

. (4)

Замечание. Уравнение (4) получено при условии, что , т.е. во всех точках гиперболы, за исключением ее вершин. Если же , то . Тогда из (4) следует, что или , что совпадает с уравнением касательной к гиперболе в её вершине. Таким образом, несмотря на то, что уравнение касательной к гиперболе в некоторой ее точке выводилось при условии, что эта точка не является вершиной, окончательное уравнение (4) подходит и для вершины тоже.

Таким же образом составим и уравнение касательной к параболе

(5)

в принадлежащей ей точке .

(5)

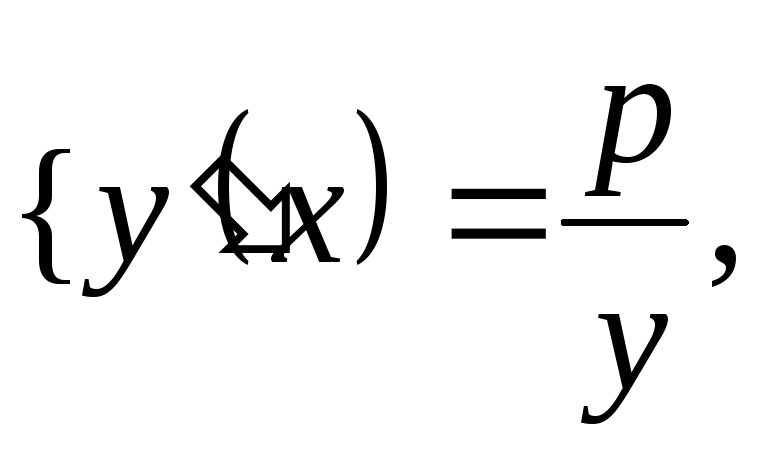
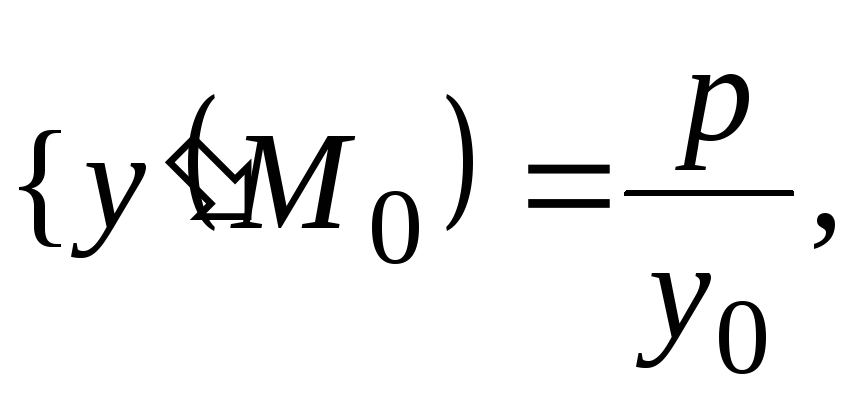
[(1)]

[точка принадлежит параболе (5)]

. (6)

Замечание. Если , то и – это вершина параболы. При условии из (6) получаем . Это уравнение оси , которая и является касательной к параболе в её вершине. Таким образом, полученное уравнение (6) задаёт касательную к параболе во всех ее точках, несмотря на то, что выводилось оно при условии .

Упражнение. Покажите, что уравнение касательной к эллипсу

в принадлежащей ему точке , имеет вид:

.