1. Збіжні послідовності

Границя числової послідовності. Число називається границею послідовності , якщо для будь-якого числа існує такий номер , що для всіх членів послідовності із номером виконується нерівність

. (2)

Якщо число є границею послідовності , то пишуть

,

а саму послідовність називають збіжною.

Послідовність, яка не є збіжною, називається розбіжною.

Приклад. Довести, що .

Доведення. Задамо довільне число і покажемо, що існує таке натуральне число , що для всіх членів послідовності із номером виконується нерівність .

Оскільки , то

.

Розв'язавши відносно нерівність , маємо .

Якщо в значенні узяти цілу частину числа , тобто покласти , то нерівність <ε виконується для всіх . Отже, .

Якщо послідовність збіжна і , то будь-який її елемент можна подати у вигляді , де - елемент нескінченно малої послідовності .

Дійсно, якщо , то послідовність є нескінченно малою, оскільки для будь-якого існує такий номер , що для виконується нерівність , тобто .

Має місце й обернене твердження. Якщо можна подати у вигляді , де  нескінченно мала послідовність, то .

Нерівність (2) рівносильна нерівності або ,

із якої випливає, що знаходиться в околі точки . Отже, означення границі числової послідовності можна дати наступним чином.

Число називається границею послідовності , якщо для будь-якого числа існує такий номер , що всі члени послідовності із номером знаходяться в околі точки .

Очевидно, що нескінченно велика послідовність не має границі. Іноді говорять, що вона має нескінченну границю і пишуть

.

Якщо при цьому, починаючи з деякого номера, всі члени послідовності додатні ( від'ємні ), то пишуть .

Усяка нескінченно мала послідовність збіжна, причому .

Це безпосередньо випливає з означення границі числової послідовності й означення нескінченно малої числової послідовності.

2. Властивості збіжних послідовностей

Теорема Збіжна послідовність має єдину границю.

Доведення. Припустимо, що збіжна послідовність має дві різні границі і , тобто . Тоді та , де і  елементи нескінченно малих послідовностей та . Отже, або Оскільки, за властивістю нескінченно малих послідовностей, є елементами нескінченно малої послідовності, а постійне число, то . Таким чином, .

Теорема. Якщо послідовність збіжна, то вона обмежена.

Доведення. Нехай і - номер, починаючи з якого виконується нерівність , де . Тоді

для всіх . Виберемо . За цієї умови для будь-якого .

Зазначимо, що не всяка обмежена послідовність є збіжною. Наприклад, послідовність обмежена, але не збіжна.

Теорема 2.6. Якщо і  збіжні послідовності, то:

1. Послідовність , яка є сумою (різницею) збіжних послідовностей та 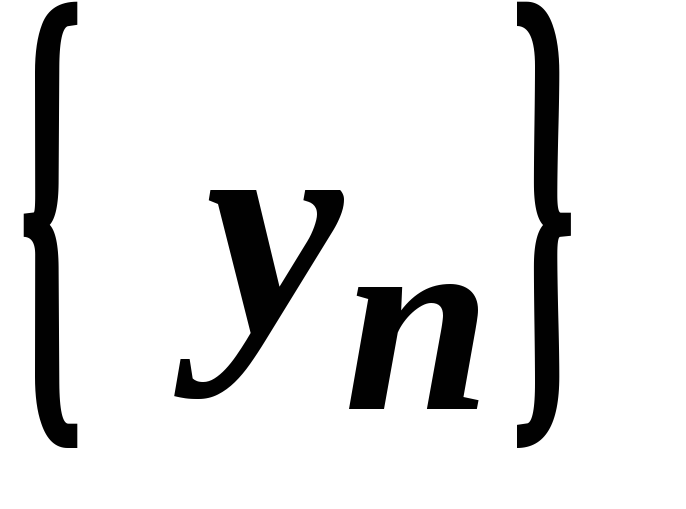, збіжна і її границя дорівнює сумі (різниці) границь цих послідовностей, тобто .

2. Послідовність , яка є добутком збіжних послідовностей й , збіжна і її границя дорівнює добутку границь цих послідовностей, тобто .

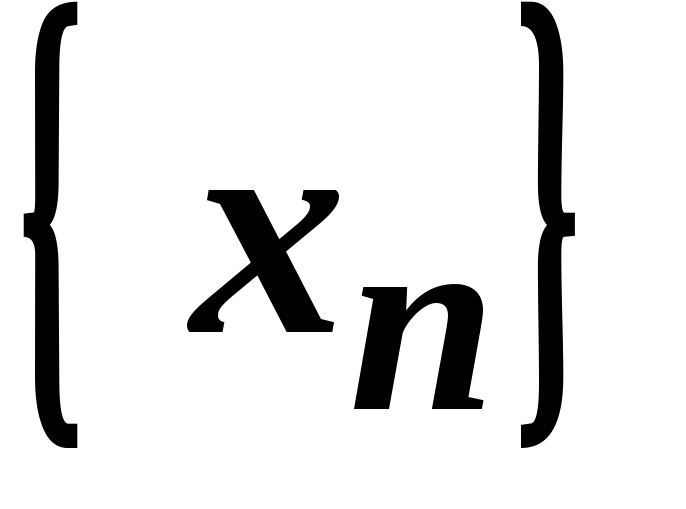3. Послідовність , яка є часткою збіжних послідовностей та , за умови , збіжна і її границя дорівнює частці границь цих послідовностей, тобто .

Доведення. Нехай і  збіжні послідовності та . Тоді і , де й – елементи нескінченно малих послідовностей і . Покажемо, що має місце:

1) .

Оскільки є елементами нескінченно малої послідовності , то звідси випливає, що .

2) .

Оскільки є елементами нескінченно малої послідовності , то .

Тобто .

3)

Послідовність є нескінченно малою. Покажемо, що послідовність обмежена. Оскільки і , то для 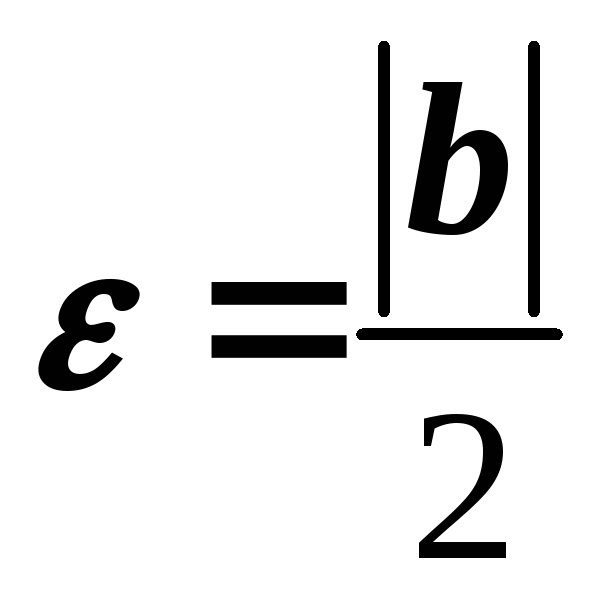існує такий номер , що для всіх виконується нерівність ,

отже, , тобто 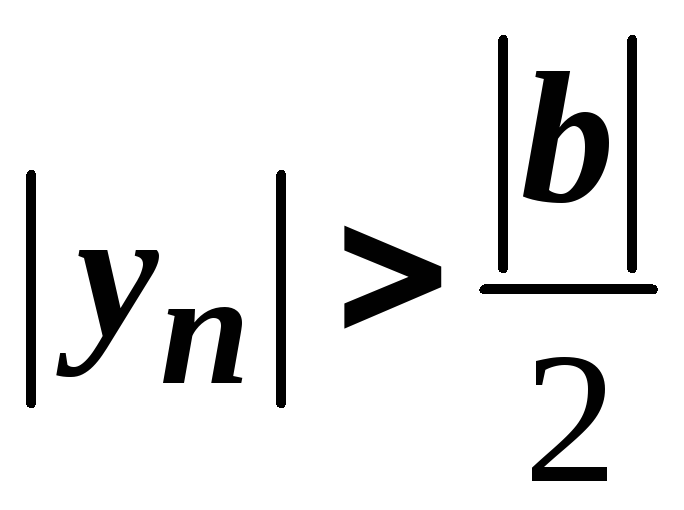, а тому 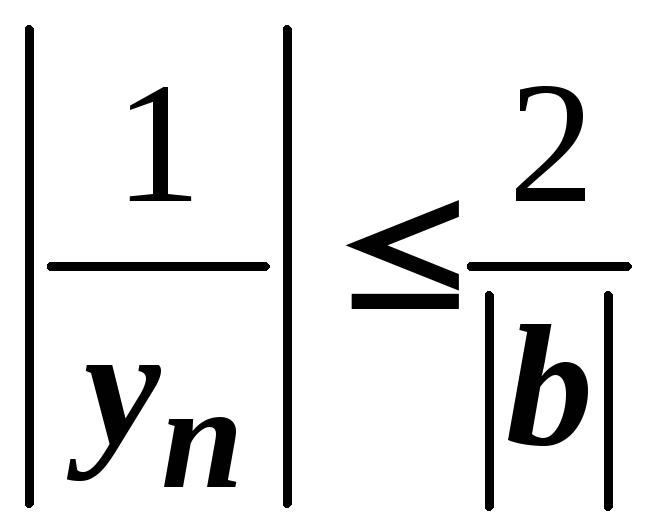для всіх . Звідси випливає, що послідовність обмежена.

Таким чином, послідовність нескінченно мала, а тому

,

тобто

, де .

Зауваження. Пункт 1) наведеної теореми допускає узагальнення на довільне скінченне число доданків. Пункт 2) - на довільне скінченне число множників. Із пункту 2) випливає, що постійний множник можна виносити за знак границі, тобто

.