Магнитомеханические явления

Найдём величину магнитного момента создаваемого током электрона p_m в атоме. Пусть электрон движется со скоростью v по орбите радиуса r . Через площадку, расположенную в любом месте на пути электрона, переносится в единицу времени заряд eν, где е – заряд электрона, а ν – число оборотов в секунду. Следовательно, движущийся по орбите электрон образует круговой ток силы . Поскольку заряд электрона отрицателен, направление движения электрона и направление тока противоположны. Магнитный момент равен:

(27.9)

так как – скорость электрона.

Момент обусловлен движением электрона по орбите, вследствие чего называется орбитальным магнитным моментом. Направление образует с направлением тока правовинтовую систему, а с направлением движения электрона левовинтовую.

Движущийся по орбите электрон обладает так же моментом импульса

,

(27.10)

где – масса, - скорость электрона.

Вектор называется орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему, следовательно, и противоположно направлены.

Отношение магнитного момента и механического для элементарной частицы называется магнитомеханическим (или гиромагнитным) отношением. Для электрона оно равно

(27.11)

где знак минус указывает на то, что направления моментов противоположны.

Вследствие вращения электрона вокруг ядра атом оказывается подобным волчку. Это обстоятельство лежит в основе магнитомеханических явлений, заключающихся в том, что намагничение магнетика приводит к его вращению и, наоборот, вращение магнетика вызывает его намагничивание.

Теорема о циркуляции вектора (для магнитного поля постоянных токов).

В магнетиках, помещенных во внеш­нее магнитное поле, возникают токи намагничивания, поэтому циркуляция вектора теперь будет определяться не только токами проводимости, но и токами намагничивания, а именно:

,

(27.12

где и — токи проводимости и намагничивания, охватываемые заданным контуром Г.

В общем случае определение токов задача сложная, формула () становится малопригод­ной в практическом отношении. Оказывается, однако, можно ввести некоторый вспомогательный вектор, цирку­ляция которого будет определяться только токами прово­димости, охватываемыми контуром Г. Действительно, из (ЖЖЖЖ) и (27.12) следует

.

(27.13)

Величину, стоящую под интегралом в скобках, обозна­чают буквой .

.

(27.14)

Величину часто называют напряженностью маг­нитного поля

Итак, есть некоторый вспомогательный век­тор , циркуляция которого по произвольному контуру Г равна алгебраической сумме токов проводимости I, охватывае­мых этим контуром:

(27.15)

Эта формула выражает теорему о циркуляции вектора : циркуляция вектора по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром.

Правило знаков для токов то же, что и в случае цир­куляции вектора .

Единицей величины является ампер на метр (А/м).

Дифференциальная форма теоремы о циркуляции вектора :

,

(27.16)

т. е. ротор вектора равен плотности тока проводимости в той же точке вещества.

Заметим, что вектор :

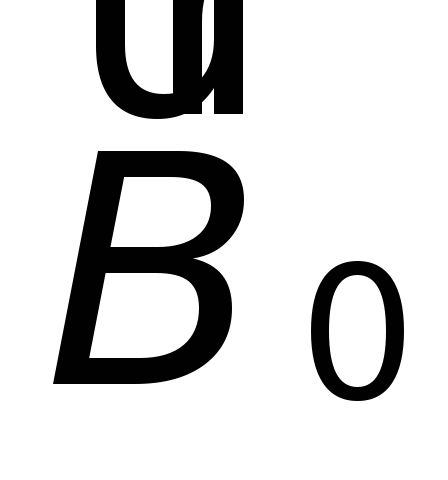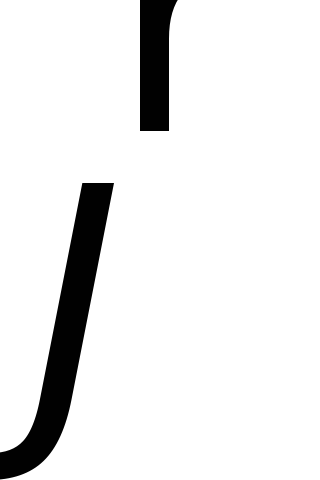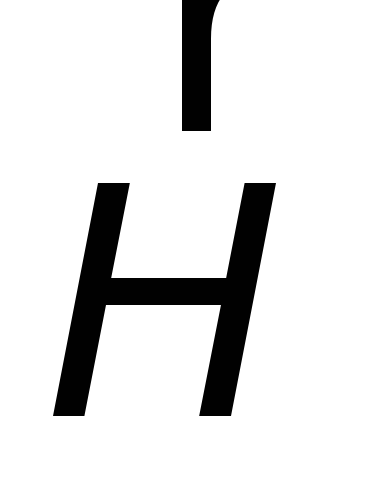1. представляет собой комбина­цию двух совершенно различных величин и . Поэто­му вектор — это вспомогательный вектор, не имеющий сколько-нибудь глубокого физического смысла;

2. за­висит, вообще говоря, от всех токов — и от токов проводимости, и от токов намагничивания

Однако важное свойство вектора , выраженное в теореме о его циркуляции, оправдывает введение этого вектора: во многих случаях он значительно упрощает изу­чение поля в магнетиках.
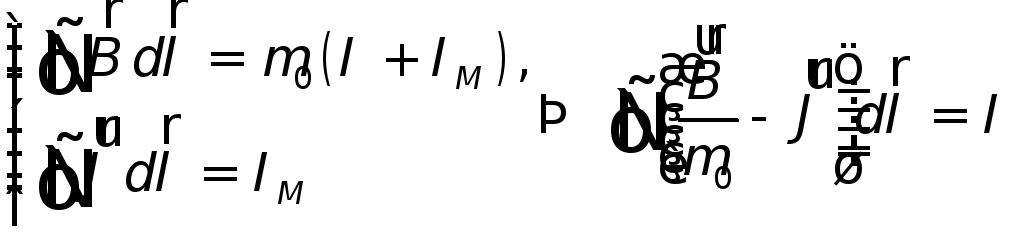