Решение практических задач

П р и м е р 1. Найти область определения функции .

Р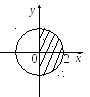ешение. Найдем область определения функции. Для этого необходимо чтобы подкоренное выражение, стоящее в знаменателе, и аргумент натурального логарифма были больше нуля, т.е.

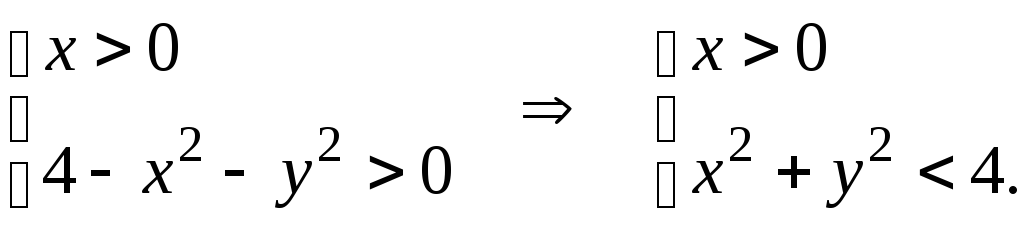
Построим область, которая получена этой системой. Так как сумма квадратов меньше 4 и x > 0, то искомой будет область заштрихованная на рисунке.

П р и м е р 2. Доказать соотношение , если .

Решение. 1) Найдем частные производные первого порядка от данной функции. Сначала найдем производную по переменной х, т. е. переменную у будем считать постоянной величиной, производная от которой равна нулю.

.

Теперь найдем производную по переменной у, т. е. переменную х будем считать постоянной величиной, производная от которой равна нулю.

.

2) Найдем вторую производную от данной функции по переменной х.

.

Найдем смешанную производную от данной функции, т. е. найдем производную по у от .

.

3) Подставим найденные значения в данное соотношение и получим

.

П р и м е р 3. Найти градиент функции в точке В (2; 4) и ее производную в точке А (– 2; 1) по направлению вектора .

Решение. 1) Для того чтобы вычислить градиент необходимо найти частные производные первого порядка от данной функции.

Сначала найдем производную по переменной х, т. е. переменную у будем считать постоянной величиной, производная от которой равна нулю.

.

Теперь найдем производную по переменной у, т. е. переменную х будем считать постоянной величиной.

.

Найдем значения найденных производных в точке А.

;

.

Подставим найденные значения в формулу нахождения градиента

.

2) Найдем значения производных, найденных в первом пункте, в точке В.

;

.

Теперь найдем направляющие косинусы вектора , координаты которого равны .

;

Подставим найденные значения в формулу нахождения производной по направлению вектора

.

П р и м е р 4. Написать уравнение касательной плоскости и нормали к поверхности в точке М₀ (2; – 3; 0).

Решение. 1) Так как функция задана явно, то уравнение касательной имеет вид

.

Найдем частные производные первого порядка в точке М₀ от данной функции

;

.

Следовательно,

2) Уравнения нормали к поверхности запишем в виде

Тогда .

П р и м е р 5. Найти экстремумы функции

Решение. Найдем критические точки. Для этого приравняем к нулю частные производные функции z.

;

;

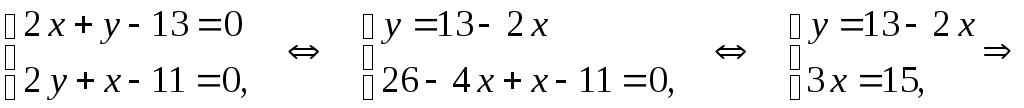
Теперь найдем вторые частные производные.

;

Исследуем точку М (5; 3). Здесь А = 2, В = 1, С = 2.

А∙С – В² = 4 – 1 = 3 > 0,

Следовательно, экстремум есть.

Так как А > 0, то в точке М функция z имеет минимум. Найдем значение функции в точке М.

Примеры для самостоятельного решения.

1. Найти область определения функций

а) ; б) .

2. Доказать соотношения:

а) , если ;

б) , если .

3. Найти градиент функции в точке В и ее производную в точке А по направлению вектора .

а) , если А (3; 2), В (5; 4);

б) , если А (3; 2; 1), В (5; 4; 2).

4. Написать уравнение касательной плоскости и нормали к поверхности в точке.

а) в точке М₀ (; 1; 0);

б) в точке М₀ (1; – 1; 5).

5. Найти экстремумы функции

а) ;

б) ;

в) ;

г) .

252