§ 3. Производные и дифференциалы высших порядков

Очевидно, что в общем случае производная f (x) является функцией. Поэтому от нее можно взять производную, т. е. выполнить операцию [f (x)].

Определение 6. Производная от первой производной f (x) называется производной второго порядка или второй производной и обозначается f (x).

Определение 7. Производной n – го порядка или n – й производной от функции f (x) называется первая производная от производной (n – 1) – го порядка и обозначается f ⁽ⁿ⁾(x).

То есть производные и дифференциалы высших порядков определяются индуктивно.

По определению дифференциала d y = f (x) ∆x, где ∆х – приращение независимой переменной – величина, не зависящая от х, а зависящая от того, какой мы ее назначим, f (x) – функция от х. Поэтому d y – функция от х, где ∆ х = const. Следовательно, от d y можно найти дифференциал.

Определение 8. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка и обозначается d ²y

d (d y) = d ²y.

Т е о р е м а 9. Дифференциал второго порядка определяется формулой

d ²y = f (x) ∆x².

.

Определение 9. Дифференциалом n – го порядка называется дифференциал от дифференциала (n – 1) – го порядка функции и обозначается d ⁿ y.

Т е о р е м а 10. Формула для нахождения дифференциала функции п – го порядка имеет вид d ⁿy = f ⁽ⁿ⁾(x)∙∆ x ⁿ, или, т. к. ∆ х = d x, то d ⁿy = f ⁽ⁿ⁾(x)∙d x ⁿ, где d x ⁿ – означает n – ю степень первого дифференциала переменной х.

Отсюда имеем, т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Замечание. Дифференциалы высших порядков не инвариантны относительно замены независимой переменной.

В этом легко убедиться при n = 2. В силу доказательства будем обозначать второй дифференциал функции у = f (x) через (d ²y)_x или (d ²y)_t, в зависимости от того, считаем ли мы независимой переменной величину х или величину t. Тогда

(d²y)_x = f (x) dx²,

между тем как х = φ (t)

Эти два выражения различны: второе содержит добавочный член, который равен нулю, если φ (t) = at + b. Таким образом, второй дифференциал инвариантен лишь относительно линейных преобразований независимой переменной.

Основные теоремы дифференциального исчисления

Т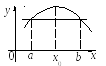 е о р е м а П ь е р а Ф е р м а [(1601 – 1665) французский математик, по профессии юрист]. Пусть функция f (x) определена в интервале (а; b), принимает в некоторой точке х = х₀ этого интервала наибольшее или наименьшее значение. Тогда, если в точке х₀ существует производная этой функции, то она равна нулю, т. е. f (x₀) = 0.

Геометрический смысл теоремы Ферма состоит в том, что если в точке х₀ дифференцируемая функция f (x) имеет наибольшее (наименьшее) значение, то в точке (х₀, f (x₀)) касательная к графику функции f (x) параллельна оси Ох.

Замечание. Теорема может быть не верна, если функцию f (x) рассматривать на отрезке [a, b]. Так как, например, f (x) = х на [0, 1] в точке х = 0 принимает наименьшее, а в точке х = 1 – наибольшее значение, однако как в той, так и в другой точке производная в ноль не обращается, а равна 1.

Т е о р е м а Р о л л я о корнях производной. Если функция f (x) непрерывна на отрезке [а, b], дифференцируема во всех его внутренних точках и на концах интервала принимает равные значения, т. е. f (а) = f (b), то ее производная обращается в ноль хотя бы в одной внутренней точке х = с этого интервала:

Г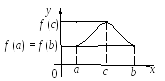еометрически теорема Ролля означает, что у графика непрерывной на отрезке [a, b] и дифференцируемой внутри него функции, принимающей на концах этого отрезка равные значения, существует точка (с; f (c)), в

которой касательная параллельна оси Ох.

Т е о р е м а Л а г р а н ж а о конечных приращениях. Если функция f (x) непрерывна на отрезке [a, b] и дифференцируема во

в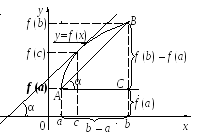сех его внутренних точках, то внутри этого отрезка найдется хотя бы одна точка х = с такая, что имеет место равенство

Геометрически теорему Лагранжа можно пояснить следующим образом: из треугольника АВС

.

Так как f (c) = tg α – есть угловой коэффициент касательной, то теорема Лагранжа утверждает, что на графике функции y = f (x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги.

Т е о р е м а К о ш и. Пусть функции f (x) и g (x) непрерывны на отрезке [a; b] и дифференцируемы на интервале (a; b). Пусть, кроме того, g (x)  0. Тогда существует точка с  (а; b), такая, что справедлива формула

Эта формула называется обобщенной формулой конечных приращений.