1.7 Шістнадцяткова система числення

Шістнадцяткова система числення, що має базис 16, використовується часто при роботі з комп’ютером, оскільки дозволяє представити двійкові числа у більш наглядній формі. Комп’ютер виконує обчислення у двійковій системі числення. Проте, є декілька зразків, коли двійковий результат представляється у шістнадцятковій системі для зручності читання. Перша можливість для комп’ютерів та програмного забезпечення, щоб позначити шістнадцятковий результат, використовувати “0x” перед шістнадцятковим числом. Кожного разу, як використовується префікс “0x”, за ним розташоване шістнадцяткове число. Наприклад 0x1234 означає 1234 у шістнадцятковій системі числення.

Базис системи 16, використовує 16 символів для представлення числових значень. Ці символи 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. “A”представляє десяткове число 10, “B” представляє 11, “C” представляє 12, “D” представляє 13, “E” представляє 14, “F” представляє 15. Приклади шістнадцяткових чисел: 2A5F, 99901, FFFFFFFF, EBACD3. Шістнадцяткове число B23CF еквівалентно 730063 у десятковій системі числення, як показано на рис. 1.10.

Рисунок 1.10 – Шістнадцяткова система числення

1.8 Конвертація з двійкової до шістнадцяткової системи числення

Така конвертація є нескладною. По-перше 1111 у двійковій - є F у шістнадцятковій, як показано на рис. 1.11. Також 11111111 це FF у шістнадцятковій. Потрібно пам’ятати один корисний факт при роботі з цими двома системами числення: для представлення однієї шістнадцяткової цифри потрібно чотири цифри у двійковій системі.

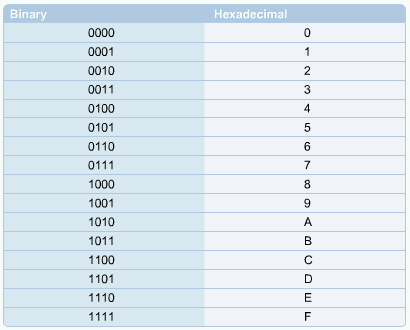
Рисунок 1.11 - Конвертація з двійкової системи числення до шістнадцяткової

Для конвертації двійкового числа у шістнадцяткову систему числення спочатку число розбивають на групи по 4 біти, починаючи від права. Потім кожну таку групу перетворюють на один шістнадцятковий символ згідно з рис. 1.11.

Наприклад розглянемо двійкове число 11110111001100010000. Виділяємо групи по 4 біти: 1111 0111 0011 0001 0000. Це число еквівалентно F7310 у шістнадцятковій системі числення, і виглядає більш зручно для читання.

Інший приклад: двійкове число 111101 групується як 11 1101. Оскільки перша група не містить 4 біти, потрібно доповнити нулями. Отримаємо 0011 1101. Шістнадцятковий еквівалент складає 3D.

1.9 Конвертація з шістнадцяткової до двійкової системи числення

Для такої конвертації використовують метод, зворотній до розглянутого у попередній секції. Кожну шістнадцяткову цифру замінюємо на 4 біта у двійковій системі. Однак, потрібно бути обережними з нулями. Наприклад, розглянемо шістнадцяткове число FE27. F це 1111, E це 1110 , 2 це 0010, 7 це 0111.

Тому результат 1111111000100111.

1.10 Конвертація у систему числення з будь яким базисом

Більшість людей звичайно знають як зробити багато різних конвертацій. Наприклад як конвертувати дюйми у ярди. Спершу потрібно розділити число дюймів на 12, щоб визначити число футів. Залишок визначає скільки дюймів у запасі. Потім, потрібно розділити число футів на 3, щоб визначити число ярдів. Залишок – число футів у запасі. Таку саму техніку використовують задля конвертації у системи числення з іншим базисом.

Наприклад, для конвертації з десяткової до вісімкової системи, потрібно ділити на 8 та записувати залишки, починаючи від останнього.

Конвертуємо 1234 з десяткової до вісімкової системи.

1234/8 = 154 R 2

154/8 = 19 R 2

19/8 = 2 R 3

2/8 = 0 R 2

Залишки від найменшого до найістотнішого дають результат у вісімковій системі числення 2322.

Щоб конвертувати у зворотному напрямку, потрібно помножувати на 8 і додавати кожну цифру, починаючи з найістотнішої.

2 * 8 = 16

16 + 3 = 19 19 * 8 = 152

152 + 2 = 154 154 x 8 = 1232

1232 + 2 = 1234

Такого ж результату можна досягти, використовуючи вагу цифри у числі:

2 x 8³ + 3 x 8² + 2 x 8¹ + 2 x 8⁰ = 1024 + 192 + 16 + 2 = 1234

Подібні методи можна використовувати для конвертації до будь якої системи числення, просто ділячи або помножуючи на базис зовнішньої системи числення.