Приложение дифференциального исчисления к исследованию функции

Пусть дана функция одной переменной .

Требуется исследовать ее методами дифференциального исчисления и построить ее график.

Для решения этой задачи рекомендуется следующая схема:

1. Найти область определения функции.

2. Исследовать функцию на четность и периодичность.

Указать симметрию графика функции относительно оси ординат, либо начала координат, если она имеет место.

3. Исследовать функцию на непрерывность, найти точки разрыва функции (если они имеются), указать их характер, исследовать поведение функции вблизи точек разрыва.

4. Найти асимптоты графика функции (если они имеются).

5. Найти точки пересечения графика функции с осями координат (если они имеются), указать интервалы знакопостоянства функции.

6. Найти точки экстремума, экстремумы функции (если они имеются), указать интервалы монотонности.

7. Найти точки перегиба графика функции (если они имеются), указать интервалы выпуклости и вогнутости.

8. Найти несколько дополнительных точек (если это необходимо) и построить график функции, пользуясь результатами проведенного исследования.

Определение. Интервалы, в которых функция только возрастает или только убывает, называются интервалами монотонности функции.

Отметим необходимые и достаточные условия возрастания и убывания функций.

Теорема 6.8 (необходимые условия). Если дифференцируемая на интервале функция возрастает (убывает), то для любого .

Теорема 6.9 (достаточные условия). Если функция дифференцируема на интервале и для любого , то эта функция возрастает (убывает) на интервале .

Определение. Точка называется точкой максимума (минимума) функции , если существует -окрестность точки такая, что для всех этой окрестности выполняется неравенство: .

Значение называют максимумом (минимумом) функции.

Определение. Точки максимума или минимума функции называют точками экстремума функции.

Экстремумы функции носят локальный характер – это наибольшее или наименьшее значения функции по сравнению с близлежащими ее значениями (рисунок 5 и рисунок 6)

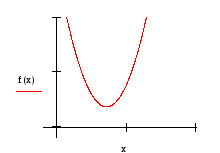
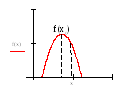
Рисунок 5 Рисунок 6

Теорема 6.10 (необходимое условие экстремума). Если дифференцируемая функция имеет экстремум в точке , то ее производная в этой точке равна нулю: .

Замечание. 1) Если , то это не значит, что – точка экстремума. 2) Существуют функции, которые в точках экстремума не имеют производной.

Например, непрерывная функция в точке не имеет производной, но точка – точка минимума этой.

Определение. Непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.

Е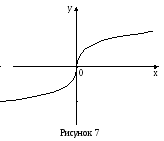сли производная в какой-либо точке равна нулю или не существует, то это не значит, что в ней функция будет иметь экстремум. В этом можно убедиться на следующем примере.

Например, для функции при производная не существует: . Экстремума нет (рисунок 7).

Экстремальные точки относятся к критическим, но не исчерпывают их, а являются только частью критических точек. Поэтому по необходимому признаку нельзя установить наличие экстремума функции в данной точке.

Теорема 6.11 (достаточное условие экстремума). Если непрерывная функция дифференцируема в некоторой -окрестности критической точки и при переходе через нее (слева направо) производная меняет знак с плюса на минус, то есть точка максимума; с минуса на плюс, то – точка минимума.

Итак, чтобы найти экстремальные точки функции одного переменного необходимо:

1. найти ее первую производную;

2. определить критические точки, т.е. найти значения аргумента, где первая производная равна нулю или не существует;

3. исследовать их на экстремум с помощью достаточного признака.

Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.

Теорема 6.12 Если в точке первая производная функции равна нулю , а вторая производная в точке существует и отлична от нуля , то при в точке функция имеет максимум и минимум при .

Пример Найти экстремумы функции .

Первая производная:

.

Критические точки:

.

Вторая производная в произвольной точке:

.

Ее значение в критических точках:

.

При функция имеет максимум, при функция имеет минимум.

Замечание. График дифференцируемой на функции не имеет изломов и заострений.

О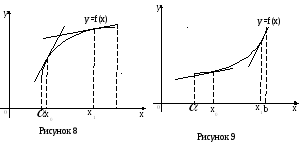 пределение. График дифференцируемой функции называется выпуклым на интервале , если дуга кривой на этом интервале расположена ниже касательной, проведенной к графику функции в любой точке (рисунок 8), в противном случае график функции называется вогнутым на интервале (рисунок 9)

Определение. Точка графика непрерывной функции , отделяющая его части разной выпуклости, называется точкой перегиба.

Интервалы выпуклости вниз и вверх находят с помощью теоремы:

Теорема 6.13 Если функция во всех точках интервала имеет отрицательную вторую производную, т.е. , то график функции в этом интервале выпуклый вверх. Если же для любого – график выпуклый вниз.

Точки перегиба графика функции находят с помощью следующей теоремы:

Теорема 6.14 (достаточное условие существование точек перегиба). Если вторая производная при переходе через точку , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой есть точка перегиба.

Например Функция при имеет точку перегиба (рисунок 10),

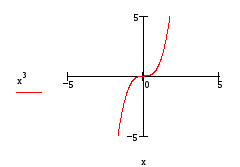
Рисунок 10 Рисунок 11

где вторая производная равна : .

Обратное утверждение неверно, т.е. если в точке вторая производная равна нулю или не существует, то это не значит, что в данной точке график функции будет иметь перегиб.

Например, для функции при вторая производная обращается в нуль: , . Однако здесь нет точки перегиба (см. рисунок 11).