129

Тема 6. Дифференциальное исчисление функций одной переменной Производная функции одной переменной

Пусть функция определена на некотором интервале . Аргументу дадим приращение : , тогда функция получит приращение . Найдем предел этого отношения при Если этот предел существует, то его называют производной функции . Производная функции имеет несколько обозначений: . Иногда в обозначении производной используется индекс , указывающий, по какой переменной взята производная.

Определение. Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (если этот предел существует):

.

Определение. Функция , имеющая производную в каждой точке интервала , называется дифференцируемой в этом интервале.

Определение. Операция нахождения производной функции называется дифференцированием.

Значение производной функции в точке обозначается одним из символов: .

Пример Найти производную функции в произвольной точке .

Решение. Значению даем приращение . Найдем приращение функции в точке : . Составим отношение . Перейдем к пределу:. Таким образом, .

Механический смысл производной. Так как или , т.е. скорость прямолинейного движения материальной точки в момент времени есть производная от пути по времени . В этом заключается механический смысл производной.

Если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса. В этом состоит физический смысл производной.

Геометрический смысл производной. Рассмотрим график непрерывной кривой , имеющий в точке невертикальную касательную. Найдем ее угловой коэффициент , где - угол касательной с осью . Для этого проведем через точку и графика секущую (рисунок 1).

Обозначим через - угол между секущей и осью . На рисунке видно, что угловой коэффициент секущей равен

.

При в силу непрерывности функции приращение тоже стремится к нулю; поэтому точка неограниченно приближается по кривой к точке , а секущая , поворачиваясь около точки , переходит в касательную. Угол , т.е. . Следовательно, , поэтому угловой коэффициент касательной равен .

Угловой коэффициент касательной к кривой

. Это равенство перепишем в виде: , т.е. производная в точке равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна . В этом заключается геометрический смысл производной.

Пример Найти угловой коэффициент касательной к графику функции в точке .

Решение. . .

Если точка касания имеет координаты (рисунок 2), угловой коэффициент касательной равен: .

У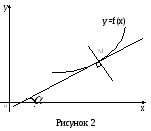равнение прямой проходящей через заданную точку в заданном направлении имеет вид: . Тогда уравнение касательной записывается в виде: .

Определение. Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.

Угловой коэффициент нормали равен: (так как нормаль перпендикулярна касательной). Уравнение нормали имеет вид: , если .

Пример Составить уравнения касательной и нормали к кривой в точке с абсциссой .

Решение. Находим . Находим производную . Так как и , то воспользуемся уравнениями и .

Подставляя найденные значения и получаем уравнения касательной , т.е. . Уравнение нормали: или .

Если функция имеет конечную производную в точке, то она дифференцируема в этой точке. Если функция дифференцируема в каждой точке интервала, то она дифференцируема в этом интервале.

Теорема 6.1 Если функция дифференцируема в некоторой точке, то она непрерывна в ней.

Обратная теорема неверна. Непрерывная функция может не иметь производной.

Пример Функция непрерывна на интервале (рисунок 3).

Решение. Производная этой функции равна

.

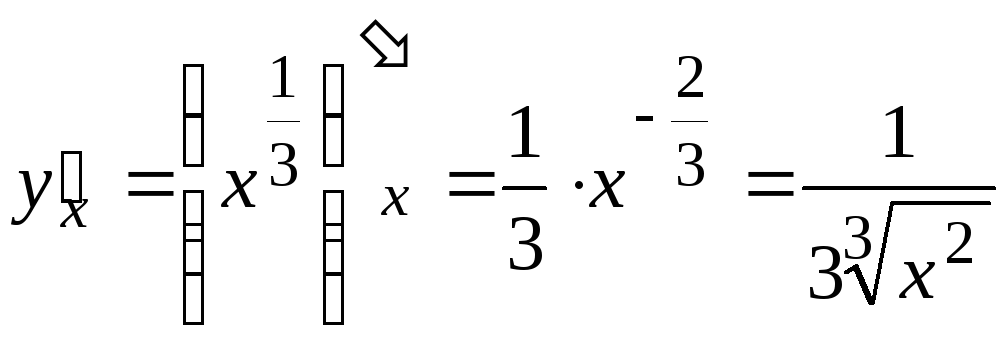
В точке - функция не дифференцируема.

Замечание. На практике чаще всего приходится находить производные от сложных функций. Поэтому в таблице формул дифференцирования аргумент заменен на промежуточный аргумент .

Таблица производных

Постоянная величина

1. ;

Степенная функция :

2. , в частности ;

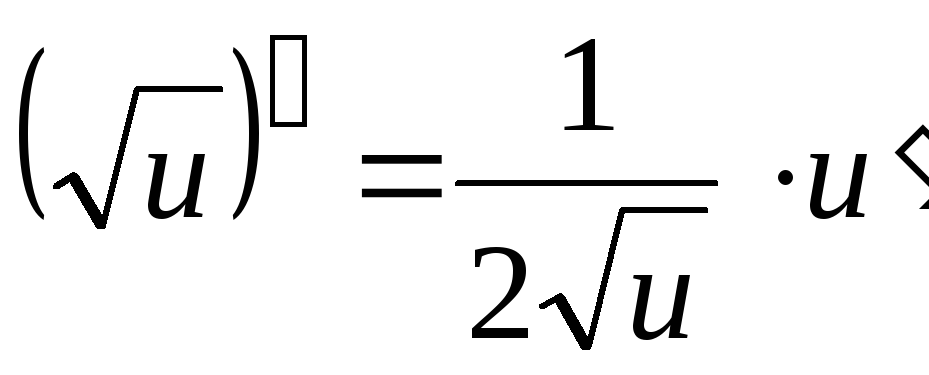Показательная функция :

3. , в частности ;

Логарифмическая функция :

4. , в частности, ;

Тригонометрические функции :

5. ;

6. ;

7. ;

8. ;

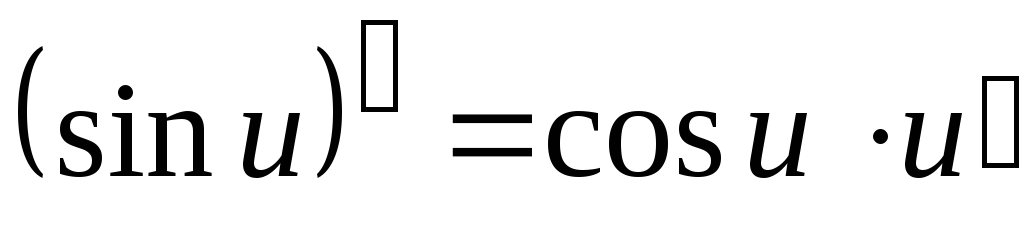Обратные тригонометрические функции , , , :

9. ;

10. ;

11. ;

12. ;

Продифференцировать функцию это значит найти ее производную, то есть вычислить предел: . Однако определение предела в большинстве случаев представляет громоздкую задачу.

Если знать производные основных элементарных функций и знать правила дифференцирования результатов арифметических действий над этими функциями, то можно легко найти производные любых элементарных функций, согласно правил определения производных, хорошо известных из школьного курса.

Пусть функции и - две дифференцируемые в некотором интервале функции.

Теорема 6.2 Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: .

Теорема справедлива для любого конечного числа слагаемых.

Пример Найти производную функции .

Решение.

.

Теорема 6.3 Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: .

Пример Найти производную функции .

Решение.

.

Теорема 6.4 Производная частного двух функций , если равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: .

Пример Найти производную функции .

Решение. .

Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу

. (1)

Это правило остается в силе, если промежуточных аргументов несколько. Так, если , , , то

. (2)

Пусть и, тогда - сложная функция с промежуточным аргументом и независимым аргументом .

Теорема 6.5 Если функция имеет производную в точке , а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке , которая находится по формуле .

Пример Найти производную функции

Решение. Применим правило дифференцирования сложной функции. Промежуточным аргументом является . Поэтому сначала следует взять производную от степенной функции по и умножить ее на производную от . Так как , то с учетом правила дифференцирования сложной функции получим: , т.е.

Производная обратной функции равна обратной величине производной данной функции:

. (3)

Пусть и - взаимно обратные функции.

Теорема 6.6 Если функция строго монотонна на интервале и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция также имеет производную в соответствующей точке, определяемую равенством или .

Пример Найти производную функции .

Решение. Пользуясь правилом дифференцирования обратной функции найдем . Обратная функция имеет производную . Следовательно, .