2 . Понятие функции

Пусть и – два непустых множества.

Определение 4.6. Функцией одной переменной называется правило, по которому каждому элементу некоторого множества соответствует единственный элемент другого множества .

– независимая переменная (аргумент),

– зависимая переменная,

– область определения функции,

– множество значений функции.

Функцию принято обозначать .

Существует несколько способов задания функции.

1. Аналитический способ. При таком способе задания функция с помощью аналитических выражений, т. е. с помощью формулы, указывающей какие действие надо совершать над значением аргумента, чтобы получить соответствующее значение функции.

Пример 4.5.

2. Табличный способ. Составляется таблица, в которой указывается ряд значений аргумента и соответствующих значений функции.

3. Графический способ. Значения функции соответствующие тем или иным значениям аргумента непосредственно находятся из графика.

4. Описательный (словесный).

Пример 4.6. Функция, ставящая в соответствие числу ее целую часть: 2,5→2; 1,3→1 (пример словесного задания функции).

Основные элементарные функции, заданные аналитически:

1. Постоянная (константа) y=C.

2. Степенная функция y=xⁿ, где n – действительное число, отличное от нуля.

3. Показательная функция .

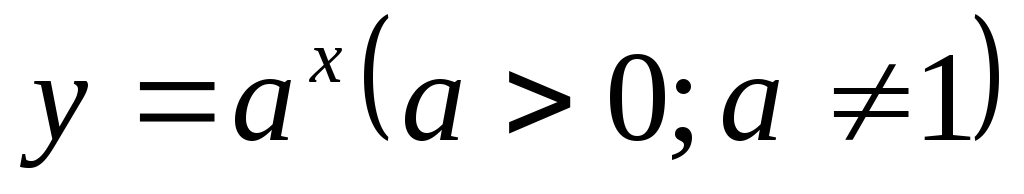4. Логарифмическая функция .

5. Тригонометрические функции .

6. Обратные тригонометрические функции – , , , .

Элементарная функция – любая функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических действий.

Определение 4.7. Сложной функцией (композицией двух или нескольких функций) называется функция вида: .

Пример 4.7. .

3. Предел функции

Понятие предела функции является обобщением понятия предела числовой последовательности, так как предел последовательности можно рассматривать как предел функции целочисленного аргумента .

Рассмотрим следующую функцию:

(4.9)

Рис. 4.4.

Если принимает только целые значения, то значения этой функции будут вести себя также как и последовательность.

При стремлении к бесконечности x значение функции будет все ближе и ближе подходить к единице, что видно из графика на рис.4.4. Это пример недостижимого предела.

Определение 4.8. Функция стремится к пределу при, если для каждого произвольного сколь угодно малого положительного числа можно указать такое положительное число N что для всех значений , удовлетворяющих неравенству будет выполняться неравенство:

(4.10)

Этот предел функции обозначается или при .

Смысл определения состоит в том, что при достаточно больших по модулю значениях x значения функции f(x) как угодно мало отличаются от числа b (по абсолютной величине).

Геометрически число есть предел функции при , если для любого найдется такое число , что для всех , таких, что , соответствующие ординаты графика функции будут заключаться в полосе , какой бы ни была эта полоса (рис.4.5).

Приведенное выше определение предела функции при предполагает неограниченное возрастание переменной по абсолютной величине. В то же время можно сформулировать понятие предела при стремление к бесконечности определенного знака, т.е. при и при . В первом случае неравенство (4.10) должно выполняться для всех x таких, что , а во втором – для всех таких, что .

Определение 4.9. Число a называется пределом функции при стремящемся к (или в точке ), если для любого, даже сколь угодно малого, числа , найдется такое число (зависящее от , ), что для всех , не равных и удовлетворяющих условию

(4.11)

выполняется неравенство:

(4.12)

Это определение называют определением предела функции по Коши. Смысл определения предела функции в точке состоит в том, что для всех значений достаточно близких к , значения функции как угодно мало отличаются от числа (по абсолютной величине).