
- •Лекция №1 теория множеств
- •1 Основные понятия теории множеств
- •Если и , то
- •2. Способы задания множеств
- •3. Универсальное множество
- •4. Операции над множествами
- •Контрольные вопросы
- •Лекция №2 теория множеств
- •1. Свойства операций над множествами
- •Если и , то
- •2. Числовые множества
- •Контрольные вопросы
- •Лекция №3 элементы математической логики
- •1. Основные понятия
- •2. Операции над высказываниями
- •3. Законы алгебры высказываний
- •4. Строение математической теоремы
- •Контрольные вопросы
- •Лекция№4 понятие предела
- •1. Предел числовой последовательности
- •2 . Понятие функции
- •3. Предел функции
- •4. Основные свойства пределов
- •5. Замечательные пределы
- •6. Способы вычисления пределов
- •Лекция №5 дифференциальное исчисление функции одной переменной
- •1. Непрерывность функции
- •2. Понятие производной
- •3. Таблица основных формул дифференцирования
- •4. Правила дифференцирования
- •5. Дифференциал
- •6. Производные высших порядков
- •7. Возрастание и убывание функции
- •Контрольные вопросы
- •Лекция №6 случайные события
- •1. Основные понятия
- •2. Классическое определение вероятности событий
- •3. Комбинаторика
- •4. Статистическая и субъективная вероятность
- •Контрольные вопросы
- •Лекция №7 основные теоремы теории вероятностей
- •1. Сложение и умножение вероятностей
- •2. Формула полной вероятности
- •3. Повторные независимые испытания
- •Контрольные вопросы
- •Лекция №8 случайные величины
- •Определение случайной величины.
- •2. Функция распределения дискретной случайной величины
- •3. Плотность распределения вероятностей
- •Контрольные вопросы
- •Лекция №9 случайные величины. Нормальный закон распределения случайной величины
- •1. Числовые характеристики случайных величин
- •2. Биномиальное распределение
- •3. Нормальное распределение
- •Контрольные вопросы
- •Лекция №10 математическая статистика
- •1. Основные понятия
- •2. Способы образования выборки
- •3. Вариационный ряд
- •4. Понятие числовых характеристик
- •Контрольные вопросы
- •Лекция №11 числовые характеристики выборки
- •1. Закон больших чисел
- •2. Выборочное распределение средних
- •3. Интервальная оценка генеральной средней
- •3. Понятия функциональной, статистической и корреляционной связи
- •Непараметрические методы оценки статистической связи
- •Контрольные вопросы
4. Операции над множествами
Если имеются некоторые множества, то из них можно получить новые с помощью определенных операций.
Определение 1.5.
Объединением двух множеств
![]() и
и
![]() называется множество, которое обозначается
называется множество, которое обозначается
![]() и состоит из элементов, принадлежащих
хотя бы одному из множеств
и состоит из элементов, принадлежащих
хотя бы одному из множеств
![]() или
или
![]() .
Наглядно это можно продемонстрировать
с помощью диаграммы Эйлера-Венна (см.
рис. 1.1а).
.
Наглядно это можно продемонстрировать
с помощью диаграммы Эйлера-Венна (см.
рис. 1.1а).
Пример 1.4.
Рассмотрим два множества
![]() и
и
![]() .
Их объединением
.
Их объединением
![]() будет множество
будет множество
![]() .
.
Определение 1.6.
Пересечением двух множеств
![]() и
и
![]() называется множество, которое обозначается
называется множество, которое обозначается
![]()
![]() и состоит из элементов, принадлежащих
каждому из множеств
и состоит из элементов, принадлежащих
каждому из множеств
![]() и
и
![]() (рис.1.1b).
(рис.1.1b).

Пример 1.5.
Рассмотрим два множества
![]() и
и
![]() .
Пересечением этих множеств
.
Пересечением этих множеств
![]() будет множество
будет множество
![]() .
.
Определение 1.7.
Разностью двух множеств
![]() и
и
![]() называется множество, которое обозначается
называется множество, которое обозначается
![]() и состоит из всех элементов
и состоит из всех элементов
![]() и не принадлежащих множеству
и не принадлежащих множеству
![]() (рис.1.1с).
(рис.1.1с).
Пример 1.6.
Рассмотрим два множества
![]() и
и
![]() .
Разностью этих множеств
.
Разностью этих множеств
![]() будет множество
будет множество
![]() .
.
Определение 1.8.
Симметричной разностью множеств
![]() и
и
![]() называется множество
называется множество
 (1.4)
(1.4)
т.е. оно состоит
из элементов, которые принадлежат либо
множеству
![]() ,
либо множеству
,
либо множеству
![]() (рис.1.1d).
(рис.1.1d).
Пример 1.7.
Рассмотрим два множества
![]() и
и
![]() .
Симметричной разностью этих множеств
.
Симметричной разностью этих множеств
![]() будет множество
будет множество
![]() .
.
Определение 1.9.
Дополнением к множеству
![]() относительно универсального множества
относительно универсального множества
![]() называется множество
называется множество
![]() (1.5)
(1.5)
На рис.1.1e приведена диаграмма Эйлера-Венна, поясняющая операцию дополнение.
Пример 1.8.
Рассмотрим множество
![]() ={
={![]() :
:
![]() ,
,
![]() – кратное
двум}. В
данном случае универсальное множество
– множество всех натуральных чисел,
т.е.
– кратное
двум}. В
данном случае универсальное множество
– множество всех натуральных чисел,
т.е.
![]() .
Тогда дополнение множества
.
Тогда дополнение множества
![]() будет множество
будет множество
![]() .
.
Контрольные вопросы
1. Сформулируйте понятие множества. 2. Какое множество называется пустым? 3. Подмножество. Какое минимальное число подмножеств имеет любое непустое множество? 4. Конечные и бесконечные множества. Приведите примеры. 5. Основные способы задания множеств? 6. Какое множество называется универсальным? 7. Сформулируйте определение операции объединение. 8. Сформулируйте определение операции пересечение. 9. Сформулируйте определение операции разность. 10. Сформулируйте определение операции симметричная разность. 11. Сформулируйте определение операции дополнение.
Лекция №2 теория множеств
План
1. Свойства операций над множествами
2. Числовые множества
1. Свойства операций над множествами
Для любых подмножеств
![]() ,
,
![]() и
и
![]() универсального подмножества
универсального подмножества
![]() справедливы следующие тождества:
справедливы следующие тождества:
1.
![]() ;
1´.
;
1´.
![]() (ассоциативные законы);
(ассоциативные законы);
2.
![]() ;
2´.
;
2´.
![]() (коммутативные законы);
(коммутативные законы);
3.
![]() ; 3´.
; 3´.
![]() (дистрибутивные законы);
(дистрибутивные законы);
4.
![]() ;
4´.
;
4´.
![]() ;
;
5.
![]() ; 5´.
; 5´.
![]() .
.
Данные свойства являются фундаментальными.
Дополнительные
свойства операций над множествами. Для
любых подмножеств
![]() и
и
![]() универсального подмножества
универсального подмножества
![]() справедливы следующие тождества:
справедливы следующие тождества:
-
Если для всех
 имеет место
имеет место
 ,
то
,
то
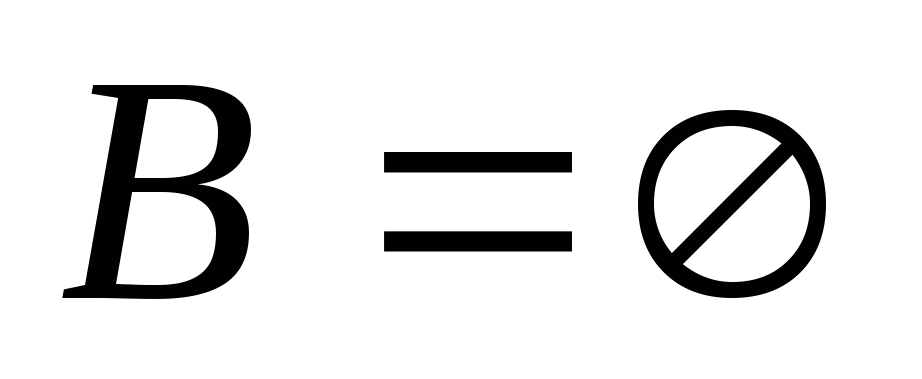 .
.
-
Если для всех
 имеет место
имеет место
 ,
то
,
то
 .
. -
Если и , то
-
 ;
; -
 ;
; -
 ;
; -
 идемпотентность;
идемпотентность; -
 идемпотентность;
идемпотентность; -
 ;
; -
 ;
; -
 закон поглощения;
закон поглощения; -
 закон поглощения;
закон поглощения; -
 закон де Моргана;
закон де Моргана; -
 закон де Моргана.
закон де Моргана.
