Контрольные вопросы

1. Какие основные задачи решает математическая статистика? 2. Генеральная и выборочная совокупность? 3. Дайте определение объема выборки. 4. Какие выборки называются репрезентативными? 5. Ошибки репрезентативности. 6. Основные способы образования выборки. 7. Понятия частоты, относительной частоты. 8. Понятие статистического ряда. 9. Запишите формулу Стэрджеса. 10. Сформулируйте понятия размаха выборки, медианы и моды. 11. Полигон частот, гистограмма. 12. Понятие точечной оценки выборочной совокупности. 13. Смещенная и несмещенная точечная оценка. 14. Сформулируйте понятие выборочной средней. 15. Сформулируйте понятие выборочной дисперсии. 16. Сформулируйте понятие выборочного среднеквадратического отклонения. 17. Сформулируйте понятие выборочного коэффициента вариации. 18. Сформулируйте понятие выборочной средней геометрической.

Лекция №11 числовые характеристики выборки

План

1. Закон больших чисел

2. Выборочное распределение средних

3. Интервальная оценка генеральной средней

4. Понятия функциональной, статистической и корреляционной связи

5. Непараметрические методы оценки статистической связи

1. Закон больших чисел

Основной закономерностью массовых случайных явлений является свойство устойчивости средних результатов.

В широком смысле слова под «законом больших чисел» понимают известное с глубокой древности свойство устойчивости массовых случайных явлений. Это свойство состоит в том, что средний результат действия большого числа случайных явлений практически перестает быть случайным и может быть предсказан с достаточной определенностью. Оно вытекает из того, что индивидуальные особенности отдельных случайных явлений, их отклонения от среднего результата в массе свей поглощаются, выравниваются.

В узком смысле слова под «законом больших чисел» понимают совокупность теорем, в которых устанавливается факт приближения средних характеристик к некоторым постоянным величинам в результате большого числа наблюдений.

Формулировка закона больших чисел, развитие идеи и методов доказательства теорем, относящихся к этому закону, принадлежат русским ученым П.Л. Чебышеву, А.А. Маркову и А. М. Ляпунову.

Теорема Чебышева (частный случай). При неограниченном увеличении числа независимых испытаний средняя арифметическая наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию, т.е. для любого положительного :

(11.10)

2. Выборочное распределение средних

Будем осуществлять испытания по схеме повторной выборки. Взяв наудачу один элемент из генеральной совокупности, мы фиксируем значения признака, возвращаем выбранный элемент в генеральную совокупность и затем выбираем наудачу следующий элемент. Этот процесс мы повторяем до получения значений, представляющих случайную выборку объема . Обозначим значения признака у первого выборочного элемента через , у второго – через , …, у го – через . Представим, что из генеральной совокупности объема произведены всевозможные выборки объема , и для каждой выборки рассчитаны выборочные средние . Естественно ожидать, что выборочные средние могут отличаться друг от друга, т.е. выборочную среднюю можно считать случайной величиной. Таким образом, полученные значения можно представить в виде ряда распределения выборочных средних и рассчитать среднее значение для этого распределения .

Любое распределение, полученное из выборочных характеристик, называется выборочным распределением. Когда мы строим распределение выборочных средних, то называем его выборочное распределение средних.

Математическое ожидание выборочной средней равно генеральной средней исследуемой совокупности :

(11.1)

Дисперсию выборочной средней можно представить:

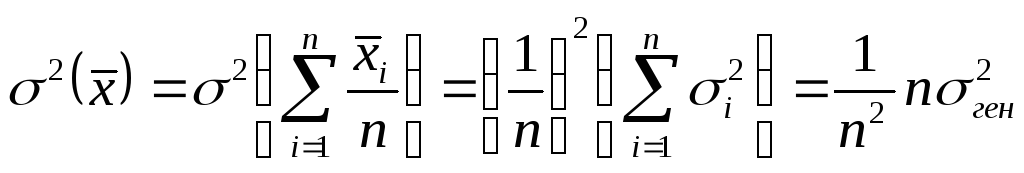(11.2)

Отсюда среднее квадратическое отклонение выборочной средней равно:

(11.3)

Теоретической основой выборочного метода служит закон больших чисел и центральная предельная теорема Ляпунова. Из теоремы Ляпунова следует, что если генеральная совокупность подчиняется нормальному закону распределения, то и выборочное распределение также подчиняется закону нормального распределения, а, согласно следствию из этой же теоремы, при достаточно большом объеме выборки распределение выборочных средних также будет подчиняться близкому к нормальному закону распределения, независимо от того, какой закон распределения имеет генеральная совокупность.