Математика и информатика. Часть I. Курс лекций. Алпатов А. В.

Лекция №1 теория множеств

План

1 Основные понятия теории множеств

2. Способы задания множеств

3. Универсальное множество

4. Операции над множествами

1 Основные понятия теории множеств

Теория множеств возникла во второй половине XIX века. Ее авторство принадлежит немецкому математику Георгу Кантору. Теория множеств лежит в основе многих математических дисциплин.

Георг Кантор (1845 – 1918). Немецкий математик. Родился в Петербурге. Окончил Берлинский университет (1867). С 1869 г. преподавал в университете в Галле (в 1879 — 1913 профессор). Сформулировал (1878) общее определение мощности множества, первое определение континуума, ввел понятия счетных и несчетных множеств, пустого множества. Развил принципы сравнения множеств. Систематическое изложение принципов своего учения о бесконечности дал в 1879 – 1884 гг. Ввел (1883) новое понятие действительных чисел.

Понятие множества является первичным и поэтому формально не может быть определено. Дадим не строгое определение, для того чтобы создать понятие, представление.

Определение 1.1. Множество – это совокупность, набор различных элементов (объектов), объединенных по каким-либо признакам, общим для них, которые позволяют их рассматривать как единое целое.

Множество состоит из элементов. Множество принято обозначать прописными латинскими буквами (), а его элементы – строчными буквами (). Если элемент принадлежит множеству , то это записывается следующим образом: . Случай, когда элемент не принадлежит множеству , записывается так: . Множество является подмножеством множества , если каждый элемент множества входит в . Записывается это в следующем виде: .

Определение 1.2. Множество называется пустым множеством, если оно не содержит ни одного элемента и обозначается .

Определение 1.3. Множества называются равными, если они состоят из одних и тех же элементов.

Пример 1.1. Множества и равны между собой.

Пример 1.2. Множества и не равны между собой.

Рассмотрим несколько утверждений без доказательств:

1. Если и , то ,

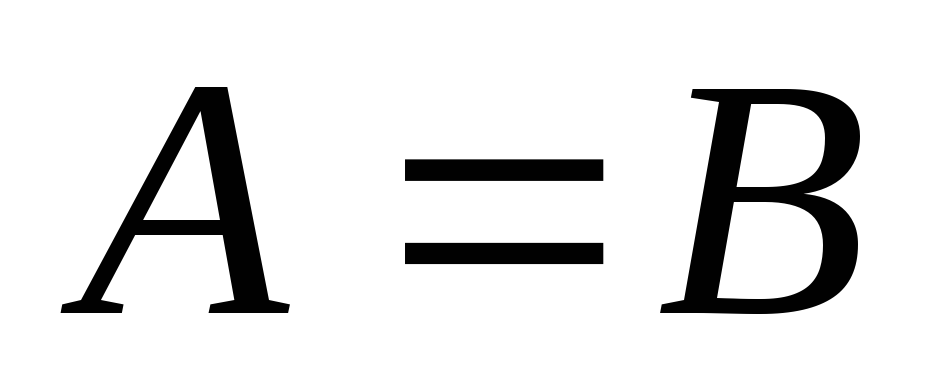2. Пустое множество есть подмножество любого множества.

3. Каждое множество имеет, по крайней мере, два различных подмножества: само себя и пустое множество.

4. Если и , то

Группа студентов – множество, элементами которого являются отдельные люди. В свою очередь, студенческая группа – есть элемент множества всех групп в университете. Таким образом, элементами множества могут быть множества.

Определение 1.4. Множество называется конечным, если содержит конечное число элементов; в случае если множество содержит бесконечное число элементов, то оно называется бесконечным.

2. Способы задания множеств

a) Конечное множество можно задать перечислением его элементов и записать в форме

(1.1)

Пример 1.2. Рассмотрим множество . Данное множество состоит из конечного числа элементов: 1, 3, 5 и 7.

b) Задание множества путем описания свойств его элементов. Описание свойств обычно задается так: пусть – утверждение, заключающееся в том, что элемент x обладает свойством . Тогда запись

(1.2)

означает, что рассматривается множество всех элементов , обладающих свойством . Таким образом, можно задать как конечные, так и бесконечные множества.

Пример 1.3. Рассмотрим множество натуральных четных чисел. Это можно записать следующим образом:

X={: , – кратное двум} (1.3)