2.5. Спектр оптичного сигналу

Розглянемо випадок, коли в початку координат знаходиться і–тий випромінювач (одна активна частка у вигляді електрона, атома і т. ін.), що безперервно випромінює одну монохроматичну хвилю. Тоді рівняння для світової хвилі (2.4) в комплексній формі запису приймає вигляд:

В дійсній формі запису цю саму хвилю можна представити таким чином:

(2.22)

В такому випадку кажуть, що таке випромінювання (не модульований сигнал) за своїм спектральним складом є світлова монохроматична хвиля з амплітудою E_mi ,частотою та фазою φ_і .

Як що одночасно випромінюють n активних часток то, оптичний сигнал, що складається з суми дискретних - монохроматичних хвиль різноманітних частот, можна записати таким чином:

(2.23)

Функція = f() зветься амплітудно-частотним спектром (рис.), а функція – фазово-частотним спектром.

В загальному випадку, коли різниця між частотами хвиль дуже мала і оптичний сигнал E(t) вже не є періодичним, то він представляється у вигляді зворотнього перетворення Фур’є:

(2.24)

де – спектральна густина амплітуд.

Спектральний склад такого оптичного сигналу можна запи­сати за допомогою прямого перетворення Фур’є :

. (2.25)

Графічно частотний спектр зображують, як розподіл потужності сигналу по частоті :

(2.27)

Для когерентного оптичного випромінювання згідно з теоремою Планшераля розподіл потужності сигналу визначається як:

, (2.28)

а для некогерентного випромінювання потужність визначається інтегралом згортки:

(2.29)

Розрізнюють три види частотних спектрів безперервний (рис.2.6.а), лінійчатий (рис.2.6.б) та змішаний (смугастий) (рис.2.6.в).

Вважають, що реальна активна частинка випромінює хвильовий цуг з експоненціальним загасанням амплітуди (2.3):

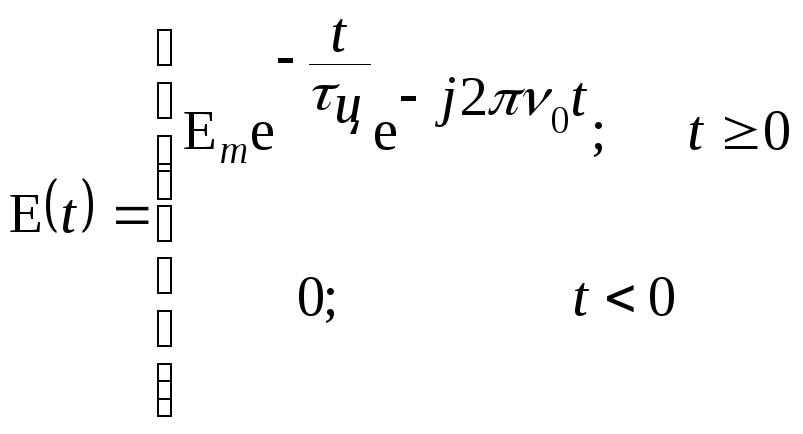(2.30)

де - постійна загасання цугу.

Форма цугу подана на малюнку (рис.2):

Знайдемо частотний спектр цугу, застосовуючи до нього пряме перетворення Фур^’є (2.25):

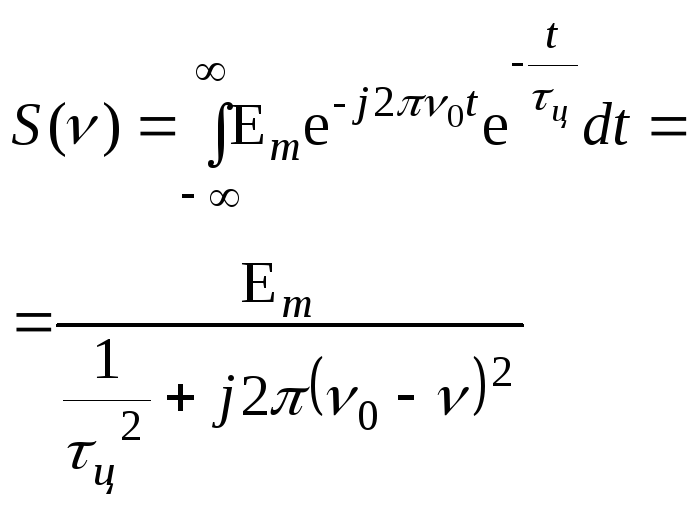(2.31)

Графік функції

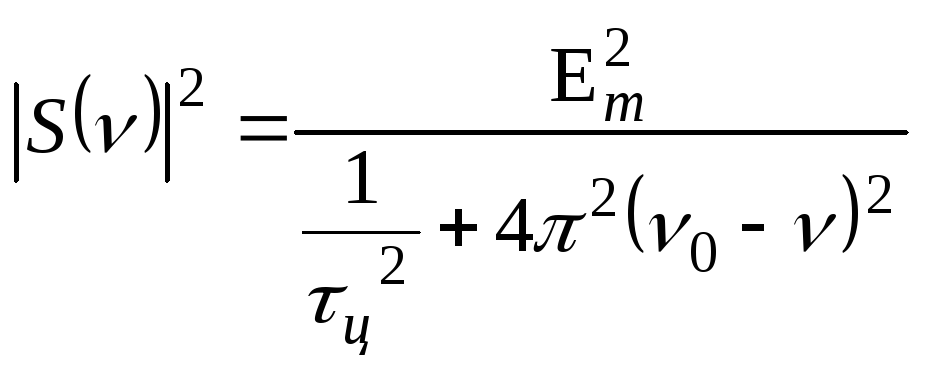(2.32)

показано на рис.2.8 .

На рис.2.5 показана напівширина спектральної лінії , яка характеризує ступінь монохроматичності випромінювання активної частинки і час когерентністі оптичного сигналу–τ_с=τ_ц= =ν^-1.