
- •Конспект лекций по теме: «Векторная алгебра и аналитическая геометрия»
- •Понятие вектора. Линейные операции над векторами.
- •Проекция вектора на ось. Свойства проекций.
- •Свойства проекций
- •Координаты вектора. Координатная запись вектора.
- •Скалярное произведение векторов и его свойства.
- •Из определения скалярного произведения и формул (2.5), (2.9) следует, что
- •Векторное произведение векторов и его свойства.
- •Свойства векторного произведения векторов
- •Смешанное произведение векторов и его свойства.
- •Аналитическая геометрия. Плоскость в пространстве.
- •Анализ общего уравнения.
- •Уравнение плоскости, проходящей через 3 точки.
- •Уравнение плоскости в отрезках.
- •Взаимное расположение двух плоскостей.
- •Прямая в пространстве.
- •Общее уравнение прямой в пространстве.
- •Переход от одних уравнений прямой к другим.
- •Взаимное расположение прямых в пространстве.
- •Взаимное расположение прямой и плоскости в пространстве.
- •Расстояния между различными объектами в пространстве.
- •Прямая на плоскости.
- •Взаимное расположение прямых на плоскости.
Взаимное расположение прямых на плоскости.
|
Каноническое
уравнение
|
Общее уравнение Ax+ By+ C= 0 |
Уравнение с угловым коэффициентом y= kx+ b |
|
Параллельность |
||
|
|
|
|
|
Перпендикулярность |
||
|
|
|
|
|
Угол между прямыми |
||
|
|
|
|
Пример. Дан прямоугольник АВС, т. А(2, 1), т. В(3, 0), т. С(-4, 2). Найти уравнение прямой АС, уравнение медианы BM, уравнение высоты BH, уравнение прямой BE параллельной АС, координаты точки H, длину высоты BH
|
Скалярное произведение |
Векторное произведение |
Смешанное произведение |
|
Определение |
||
|
число
а•b=│а│·│b│cos φ |
ab= вектор с, что 1 │с│=│a│·│b│sin φ, где = a,b 2 вектор ca, cb, т.е. с плоскости, в которой лежат вектора а и b. 3 кратчайший поворот от вектора a к b, видимый с конца вектора с будет против часовой стрелки. |
число
аbc= (ab) • с |
|
Свойства |
||
|
1° a • b = b • a 2° a • b= 0, т.к. a ┴ b 3° (λa)• b= λ(a• b) 4° a•(b + c)= a• b + a• c 5° а • а= │a│2 |
1 антикоммунитативность ab= -ba 2 (λa)b= λ (ab) 3 a(b + с)= ab + aс 4 a а= 0 |
1° abc= - bac= bca= ... 2° (λa)bc= λ(abc) 3° (a+ b) cd= acd+ bcd 4° ijk= (i×j)· k= k· k= │k│2= 1 ijk= 1 |
|
Вычисление в координатной форме |
||
|
a•b= ax bx + ay by + az bz |
|
|
|
Приложения |
||
|
1) 2) - острый, cos>0, отсюда следует: a•b> 0. - тупой, cos<0, отсюда следует: a•b< 0. =90, cos=0, отсюда следует: a•b= 0. 3)
|
1) Sпар=│a b│ 2) 3) a║b, отсюда следует, что │ ab│= 0.
|
1) Vпарал= │abc│ 2)
Vтетр= Vтетр
= 3) если abc>0, то тройка векторов правая; если abc<0, то тройка векторов левая. 4) abc – компланарные: abc=0.
|

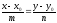
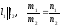
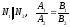
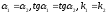
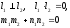
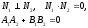
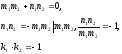
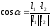
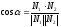
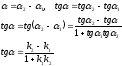
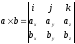
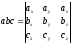
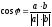
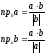
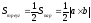
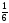 Vпарал
Vпарал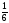 │abc│
│abc│