Прямая в пространстве.

Определение: Любой ненулевой вектор, параллельный прямой, называется направляющим вектором этой прямой.

l= (m; n; p) ║прямой.

Пусть т. М₀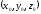- произвольная фиксированная точка прямой,

т. М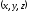- текущая фиксированная точка прямой.

Вектор М₀М= 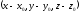║ l= (m; n; p).

Координаты векторов М₀М и l пропорциональны.

- каноническое уравнение прямой в пространстве.

Положим в канонических уравнениях все равно параметру t и выразим x, y, z:

_.

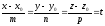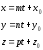; - параметрические уравнения прямой в пространстве.

Задавая различные значения параметра t из параметрических уравнений можно получать точки, принадлежащие прямой.

Аксиома: Через две различные точки проходит одна прямая.

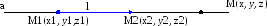
Прямая а проходит через М₁, М₂. М₁М и М₁М₂ – направляющие векторы.

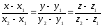- уравнение прямой, проходящей через две точки.

Общее уравнение прямой в пространстве.

Прямая может быть задана в пространстве как линия пересечения плоскостей:

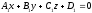
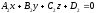- общее уравнение прямой в пространстве.

Замечание: такое задание прямой неоднозначно.

Для нахождения направляющего вектора прямой, нужно провести следующие рассуждения:

l  N₁

l  N₂ l= N₁ ×N₂.

Для нахождения точки, принадлежащей прямой, нужно в общих уравнениях одну координату обнулить, например, положить х=0 и вычислить из системы у,z. Если известен, направляющий вектор прямой и точка, принадлежащая прямой, то такая прямая называется заданной, т.е. можно составить ее каноническое уравнение.

Переход от одних уравнений прямой к другим.

1) От канонических к параметрическим.

_.

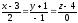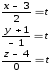
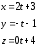
2) От параметрических к каноническим.

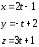
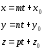
l= (2,-1,3), т. М₀= (-1,2,1).

_.

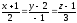3)От общих к каноническим.

2x - y + z - 3=0 N₁=(2, -1, 1),

x - 3y - z - 2=0 N₂= (1, -3, -1).

l  N₁

l  N₂ ,

l= N₁ ×N₂=

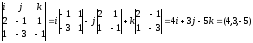
Пусть х=0, тогда -y + z - 3= 0 +

-3y - z - 2= 0

-4y – 5= 0

y= 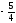, z=

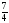
т. М₀= .

_.

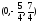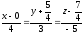Взаимное расположение прямых в пространстве.

1) Прямая (1) c направляющим вектором l₁= (m₁, n₁, p₁) ║ прямой (2) c направляющим вектором l₂=(m₂, n₂, p₂).

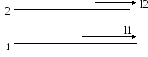
l₁ ║ l₂. Отсюда следует, что 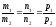- условие параллельности двух прямых в пространстве.

2) Прямая (1)  прямой (2).

l₁  l₂. Отсюда следует: l₁• l₂=0.

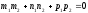- условие перпендикулярности двух прямых в пространстве.

3) Угол между двумя прямыми - это угол между их направляющими векторами.

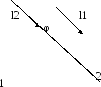
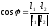- угол между прямыми.

Взаимное расположение прямой и плоскости в пространстве.

Возьмем в пространстве плоскость α с уравнением ,

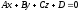N= (A, B, C), и прямую а с уравнением 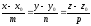, l= (m; n; p).

Возможны следующие случаи расположения:

1) Прямая  плоскости.

N║l: 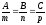- условие перпендикулярности прямой и плоскости.

2) Прямая ║ плоскости.

N  l. N•l = 0: Am + Bn + Cp= 0 - условие параллельности прямой и плоскости.

3) Прямая лежит в плоскости.

N  l, т. М₀ на прямой Є плоскости.

N•l = 0, координаты т. М₀ удовлетворяют уравнению плоскости.

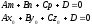- условие принадлежности прямой к плоскости.

4) Угол между прямой и плоскостью - это угол между прямой и ее проекцией на плоскость.

; .

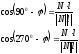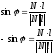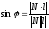- угол между прямой и плоскостью в пространстве.

Пример. Найти угол между прямой и плоскостью, при этом ,

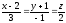l = (3, -1, 2), N =(2, -1, 1).