- •Конспект лекций по теме: «Векторная алгебра и аналитическая геометрия»
- •Понятие вектора. Линейные операции над векторами.
- •Проекция вектора на ось. Свойства проекций.
- •Свойства проекций
- •Координаты вектора. Координатная запись вектора.
- •Скалярное произведение векторов и его свойства.
- •Из определения скалярного произведения и формул (2.5), (2.9) следует, что
- •Векторное произведение векторов и его свойства.
- •Свойства векторного произведения векторов
- •Смешанное произведение векторов и его свойства.
- •Аналитическая геометрия. Плоскость в пространстве.
- •Анализ общего уравнения.
- •Уравнение плоскости, проходящей через 3 точки.
- •Уравнение плоскости в отрезках.
- •Взаимное расположение двух плоскостей.
- •Прямая в пространстве.
- •Общее уравнение прямой в пространстве.
- •Переход от одних уравнений прямой к другим.
- •Взаимное расположение прямых в пространстве.
- •Взаимное расположение прямой и плоскости в пространстве.
- •Расстояния между различными объектами в пространстве.
- •Прямая на плоскости.
- •Взаимное расположение прямых на плоскости.
Из определения скалярного произведения и формул (2.5), (2.9) следует, что
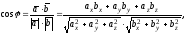 (2.10)
(2.10)
где
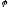 угол между векторами
угол между векторами
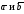 .
.
-
Вычисление проекции одного вектора на другой
Из равенств (2.8) находим:
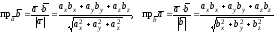 .
.
-
Условие перпендикулярности векторов
Используя свойство 1о и формулу (2.9) , получаем:
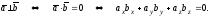
Векторное произведение векторов и его свойства.
Упорядоченная
тройка векторов
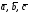 называется правой,
если кратчайший поворот первого вектора
ко второму виден
из конца
третьего вектора против часовой стрелки,
в противном случае тройка векторов
называется левой.
называется правой,
если кратчайший поворот первого вектора
ко второму виден
из конца
третьего вектора против часовой стрелки,
в противном случае тройка векторов
называется левой.
Векторным
произведением
двух векторов
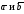 называется третий вектор
называется третий вектор
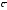 ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
а)
длина вектора
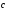 вычисляется по формуле:
вычисляется по формуле:
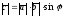 ,
,
где
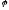 угол между векторами
угол между векторами
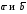 .
.
Б)
вектор
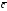 перпендикулярен векторам
перпендикулярен векторам
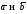 ;
;
в)
тройка векторов
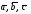 правая.
правая.
Обозначение:
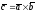 или
или
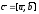 .
.
Свойства векторного произведения векторов
1°.
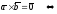
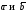 – коллинеарные векторы;
– коллинеарные векторы;
2°.
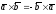 ;
;
3°.
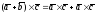 ;
;
4°.
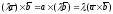 .
.
Доказательство
Свойство 1°
Если
хотя бы один из векторов нулевой, то
свойство очевидно. Пусть
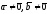 ,
тогда:
,
тогда:
если
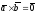 ,
то
,
то
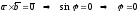 ,
либо
,
либо
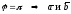 – коллинеарны;
– коллинеарны;
если
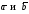 коллинеарны,
коллинеарны,
то
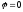 ,
либо
,
либо
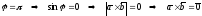 .
.
Свойство 2о
Пусть
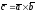 .
Из определения векторного произведения
векторов следует:
.
Из определения векторного произведения
векторов следует:
1)
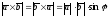 ;
;
2)
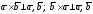 ;
;
3)
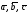 – правая тройка
– правая тройка
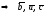 – левая тройка
– левая тройка
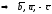 – правая тройка. Отсюда получаем:
– правая тройка. Отсюда получаем:
 .
.
Свойства 3о, 4° доказать самостоятельно.
Найдем векторные произведения ортов осей координат:
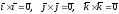 (свойство
1°);
(свойство
1°);
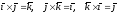 (правые
тройки векторов);
(правые
тройки векторов);
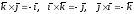 (левые
тройки векторов).
(левые
тройки векторов).
Используя
полученные равенства, выразим векторное
произведение через координаты
сомножителей. Пусть
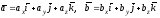 ,
тогда, используя свойства 1о
– 4°, получаем:
,
тогда, используя свойства 1о
– 4°, получаем:
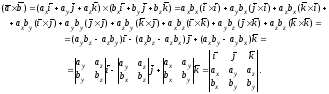
Таким образом,
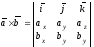 .
.
(2.11)
Основные приложения векторного произведения.
-
Вычисление площади треугольника (параллелограмма). Из курса математики средней школы известно, что площадь треугольника равна половине произведения его сторон на синус угла между ними, что совпадает с половиной модуля векторного произведения векторов, которые построены на сторонах треугольника. Таким образом,

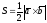 ,
,
где
S площадь
треугольника с вершинами в точках А,
В,
С,
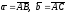 (рис. 2.9). 2) Вычисление высоты треугольника
(параллелограмма).Вычислим
площадь треугольника
двумя
способами:
(рис. 2.9). 2) Вычисление высоты треугольника
(параллелограмма).Вычислим
площадь треугольника
двумя
способами:
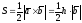 ,
,
где h – высота треугольника, опущенная из вершины В (рис. 2.9). Из этого равенства получаем:
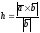 .
.
Пример. 2.1. Найти площадь треугольника с вершинами в точках А(1, 1, 1), В(1, 2, 3), С(3, 2, 1) и высоту, опущенную из вершины В на сторону АС (рис. 2.9).
Решение.
Пусть
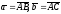 ,
тогда
,
тогда
Смешанное произведение векторов и его свойства.
Пусть
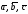 – три произвольных вектора.
– три произвольных вектора.
Три вектора называются компланарными, если они параллельны одной плоскости, т.е., будучи приведены к одному началу, лежат в одной плоскости.
Смешанным
произведением
векторов
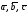 называется число равное скалярному
произведению векторного произведения
векторов
называется число равное скалярному
произведению векторного произведения
векторов
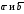 на вектор
на вектор
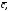 т.е.
т.е.
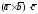 Геометрический смысл смешанного
произведения определяется следующей
теоремой.
Геометрический смысл смешанного
произведения определяется следующей
теоремой.
Теорема
2.1. Смешанное
произведение
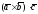 равно объему параллелепипеда V,
построенного на векторах
равно объему параллелепипеда V,
построенного на векторах
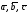 ,
взятому со знаком "+", если тройка
векторов
,
взятому со знаком "+", если тройка
векторов
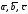 правая, и со знаком "–", если тройка
векторов
правая, и со знаком "–", если тройка
векторов
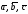 левая. Если векторы
левая. Если векторы
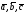 компланарны, то смешанное произведение
рано нулю, т.е.
компланарны, то смешанное произведение
рано нулю, т.е.
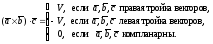
Доказательство
Пусть
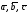 – некомпланарные векторы, образующие
правую тройку. Обозначим через V
объем параллелепипеда, построенного
на векторах
– некомпланарные векторы, образующие
правую тройку. Обозначим через V
объем параллелепипеда, построенного
на векторах
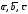 ,
через S
– площадь параллелограмма, построенного
на векторах
,
через S
– площадь параллелограмма, построенного
на векторах
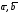 ,
через h
– высоту параллелепипеда, опущенную
из конца вектора
,
через h
– высоту параллелепипеда, опущенную
из конца вектора
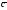 ,
через
,
через
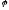 – угол между векторами,
– угол между векторами,
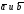 ,
через
,
через
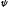 – угол между векторами
– угол между векторами
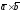 и
и
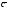 (рис. 2.10). Тогда по определению скалярного
и векторного произведений векторов
находим:
(рис. 2.10). Тогда по определению скалярного
и векторного произведений векторов
находим:
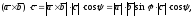
но
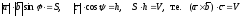 .
.
Пусть
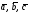 – некомпланарные векторы, образующие
левую тройку, тогда векторы
– некомпланарные векторы, образующие
левую тройку, тогда векторы
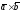 и
и
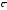 образуют угол, равный
образуют угол, равный
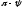 ,
при этом
,
при этом
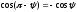 ,
следовательно:
,
следовательно:
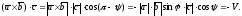
Пусть
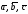 компланарны. Если
компланарны. Если
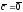 ,
то утверждение очевидно. Пусть
,
то утверждение очевидно. Пусть
 ,
тогда либо
,
тогда либо
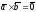 (если векторы
(если векторы
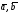 коллинеарны) и
коллинеарны) и
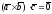 ,
либо
,
либо
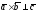 и тогда
и тогда
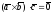 .
.
Верно
и обратное последнему утверждение,
т.е., если
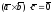 ,
то векторы
,
то векторы
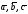 компланарны. Действительно, если
компланарны. Действительно, если
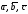 некомпланарны, то по теореме 2.1
некомпланарны, то по теореме 2.1
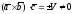 ,
что противоречит условию
,
что противоречит условию
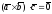 .
.
Теорема 2.2. В смешанном произведении векторов знаки векторного и скалярного произведений можно поменять местами, т.е.
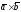
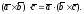
Доказательство. По свойству 2° скалярного произведения имеем:
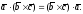
По теореме 2.1
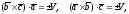 (2.12)
(2.12)
причем
тройки векторов
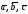 и
и
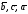 одинаково ориентированы, т.е. если
одинаково ориентированы, т.е. если
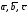 правая тройка, то и
правая тройка, то и
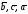 правая тройка, если
правая тройка, если
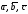 левая тройка, то и
левая тройка, то и
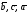 левая тройка. Следовательно, в правых
частях равенств (2.12) знаки одинаковые,
т.е.
левая тройка. Следовательно, в правых
частях равенств (2.12) знаки одинаковые,
т.е.
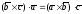 или
или
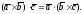
Так
как справедлива теорема 2.2, смешанное
произведение обозначают символом
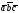 .
.
Найдем выражение смешанного произведения векторов через координаты сомножителей. Пусть
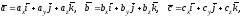
тогда по формулам (2.9), (2.11) находим:
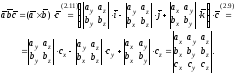
Основные приложения смешанного произведения векторов
1)
Вычисление объема тетраэдра
(параллелепипеда), построенного на
векторах
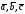 (рис. 2.10).Если векторы
(рис. 2.10).Если векторы
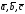 некомпланарны, то по теореме 2.1
некомпланарны, то по теореме 2.1
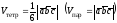 .
(2.13)
.
(2.13)
2) Вычисление высоты тетраэдра (параллелепипеда) (рис. 2.10). Вычислим объем тетраэдра двумя способами:
с одной стороны,
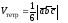 ,
,
с другой стороны,
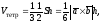
отсюда
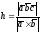 (высота параллелепипеда такая же);
(высота параллелепипеда такая же);
3) Условие компланарности векторов (теорема 2.1):
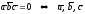 – компланарны.
– компланарны.
Пример.
Вычислить
объем тетраэдра с вершинами в точках
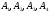 и его высоту, опущенную из вершины
и его высоту, опущенную из вершины
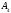 на грань
на грань
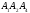
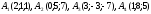
Решение.
Из вершины
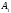 проведем векторы
проведем векторы
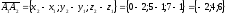
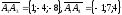
Вычислив смешанное произведение векторов:
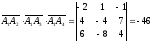
находим объем пирамиды согласно формуле:
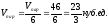 ,где
,где
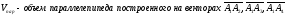
Высоту пирамиды можно вычислить по формуле:
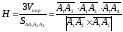 ,
где
,
где
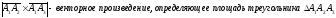
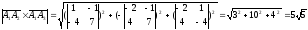
Таким образом, высота пирамиды равна: