ЛАБОРАТОРНАЯ РАБОТА № 6

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ВОЗДУХА МЕТОДОМ НАГРЕТОЙ НИТИ

Цель работы: экспериментальное определение теплопроводности воздуха, находящегося вокруг нагретой электрическим током нити.

Приборы и оборудование: функциональный модуль в отдельном корпусе, универсальный приборный модуль в отдельном корпусе, мультиметр, соединительные провода, термометр.

1. Теоретическое введение

1.1. Уравнение теплопроводности

Тела, находящиеся при различных температурах, могут обмениваться внутренней энергией. Перенос энергии, теплообмен – это самопроизвольный, необратимый процесс распространения тепла в пространстве, обусловленный разностью температур.

Различаются три основных способа переноса тепла.

1. Теплопроводность – перенос, обусловленный взаимодействием микрочастиц соприкасающихся тел, имеющих равную температуру.

2. Конвекция – перенос вследствие пространственного перемещения вещества.

3. Тепловое излучение – перенос посредством электромагнитного поля с двойным взаимным превращением теплоты в энергию поля и наоборот.

В реальных тепловых процессах, как правило, перенос тепла осуществляется одновременно тремя способами. В данной работе изучается первый из них.

При отсутствии конвекции (макроскопического перемешивания теплых и холодных масс воздуха) перенос тепла происходит благодаря теплопроводности, связанной с тепловым движением молекул. Молекулы при этом обмениваются энергией, поэтому в основе теплопроводности лежит процесс переноса энергии.

Плотностью потока тепла называется вектор , совпадающий по направлению с направлением распространения тепла и численно равный количеству тепла, проходящему в единицу времени через единичную площадь перпендикулярную к направлению потока. В рассматриваемой среде вектор может быть функцией, как координат, так и времени: . Можно показать, что

, (1)

где – плотность вещества, – удельная теплоемкость, – температура среды. Опытным путем установлено, что если на разных сторонах плоскопараллельной пластины толщиной поддерживать температуры и , то тепловой поток распространяется в направлении от большей температуры к меньшей и равен

, (2)

где – коэффициент теплопроводности, зависящий только от свойств среды и ее физического состояния. Переходя к пределу , получим закон Фурье для плотности теплового потока

. (3)

Подставляя (3) в (1) получим уравнение теплопроводности

. (4)

1.2. Описание экспериментальной установки и вывод расчетной формулы

На передней панели модуля расположены крепежный винт 1, табличка с названием работы 2, корпус термостата 5, гнезда 3 и 4 для подключения источника питания и мультиметра (вольтметра), тумблер для подключения вольтметра (рис. 1).

Принцип работы установки состоит в следующем. Нагреваемая вольфрамовая нить (9) находится в цилиндрическом стеклянном баллоне с двойными стенками, между которыми находится вода. Температура воды и, следовательно, внутренней стенки баллона считается постоянной в течение опыта. Вольфрамовая проволока через гнезда 3 и соединительные провода подключается к источнику питания постоянного тока приборного модуля. Ток в нити определяется по падению напряжения на балластном сопротивлении . Напряжение на проволоке и падение напряжения на балластном сопротивлении измеряется мультиметром (вольтметром) модуля, подключенным с помощью соединительных проводов к гнездам 4 при соответствующем положении переключателя 6 (рис.1).

При нагревании нити создается разность температур вдоль радиуса трубки. Если разность температур поддерживать постоянной, то возникнет стационарное неравновесное состояние, при котором переносимый тепловой поток не изменяется. Для плотности теплового потока , рассеиваемого за время через цилиндрическую поверхность площадью можно записать следующее соотношение (закон Фурье)

, (5)

где и – радиус и длина цилиндра, – коэффициент теплопроводности воздуха, – температура воздуха.

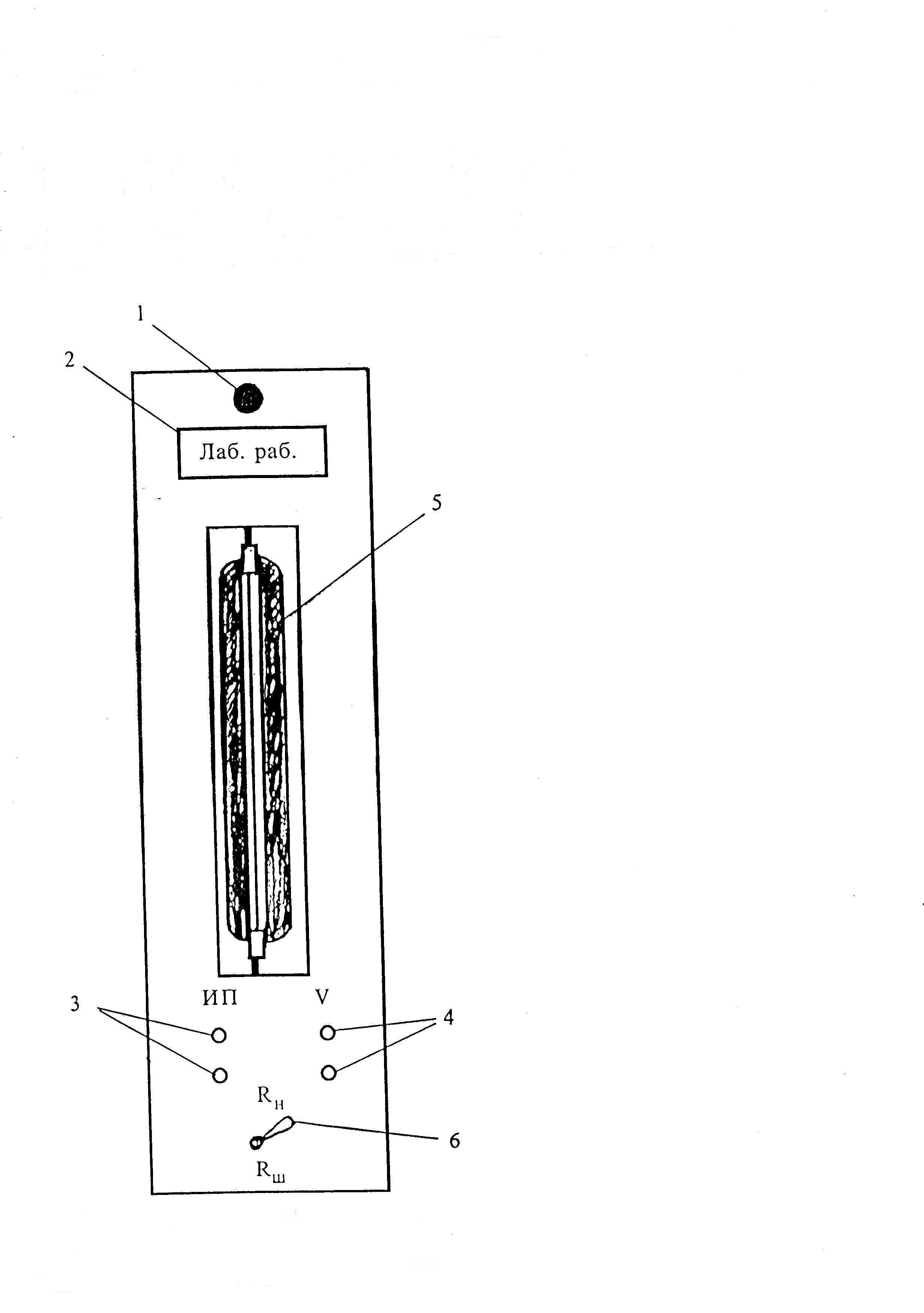
Рис. 1. Вид и устройство экспериментального модуля.

Из уравнения (5) получим выражение для мощности теплового потока, излучаемого цилиндрической поверхностью радиуса через цилиндрическую поверхность радиуса

. (6)

Условия эксперимента поддерживаются таким образом, что рассматриваемую задачу можно считать стационарной – температура не меняется во времени, т.к. температура нити и температура внутренней стенки постоянны. Запишем уравнение теплопроводности для однородной среды с цилиндрической симметрией при стационарных условиях

. (7)

Воспользовавшись формулой (5) можно показать, что

, (8)

а следовательно

, (9)

т.е.

, (10)

где константы и могут быть определены из граничных условий

(11)

откуда получим, что

. (12)

Используем полученный результат для взятия интеграла в формуле (6). Заметим, что подынтегральное выражение совпадает с (9), а значит, не зависит от . Таким образом, для мощности теплового потока с учетом получим следующее выражение

. (13)

Здесь мы также предположили, что коэффициент теплопроводности воздуха не зависит от температуры.

Опыт производится при постоянной температуре трубки 9 (рис. 1), равной . При этом увеличение электрической мощности, выделяемой в нити, на величину приводит к возрастанию ее температуры на . Поэтому из (13), с учетом закона сохранения энергии можно записать:

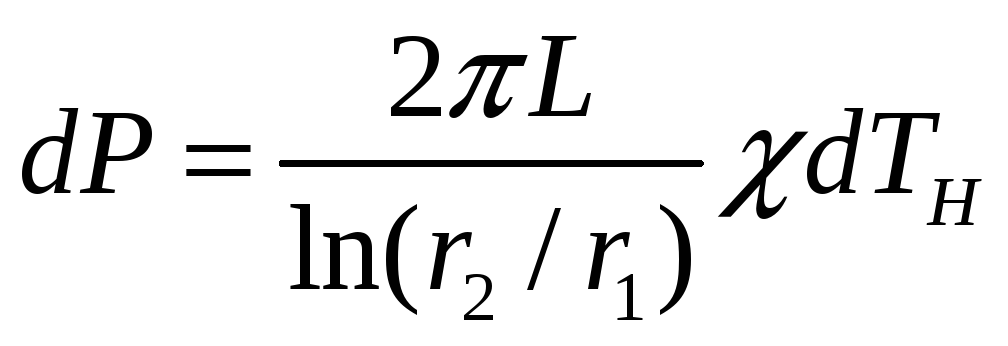(14)

Так как вблизи нити теплопроводность воздуха определяется температурой нити, то в (14) величина относится к температуре . Поэтому при возрастании температуры нити на дополнительный перенос тепловой мощности от нити к стенке трубки определяется только теплопроводностью слоя воздуха вблизи нити. Из соотношения (14) получим:

(15)

Для определения производной необходимо знать зависимость , которую находят по экспериментальным данным. Мощность теплового потока находится по напряжению , измеренному на нити, и току , текущему через балластном сопротивление и нить. Для определения тока измеряется напряжение на балластном сопротивлении . Температура нити определяется из соотношения:

(16)

где: - сопротивление нити при t = 0^оС, Ом;

- сопротивление нити при температуре опыта, Ом;

- температурный коэффициент сопротивления материала нити, 1/ ⁰С.

Формула (15) позволяет по найденной экспериментальной зависимости определить .

Дифференцируя (16), получаем:

(17)

Подставляя из (17) в (15) получаем:

(18)

Формула (18) является конечной расчетной формулой и позволяет использовать график зависимости (рис. 2) для нахождения производной .

Рис. 2. График зависимости мощности теплового потока от сопротивления нити.