1.4. Определение коэффициента вязкости жидкости методом падающего шарика
Рассмотрим свободное падение тела внутри покоящейся жидкости. При соприкосновении твёрдого тела с жидкостью к поверхности тела притягиваются молекулы жидкости, образуя молекулярный слой, который движется вместе с телом со скоростью его движения. Он увлекает соседние молекулы. Более удаленные от тела слои жидкости движутся более медленно, более близкие к телу – более быстро. В этих условиях между слоями, движущимися с различными скоростями, действуют силы внутреннего трения. Силы внутреннего трения, действующие со стороны удаленных слоев на прилегающие к телу частицы, тормозят движение тела, являясь силами сопротивления. Они направлены в сторону, противоположную перемещению тела.
Опыты показывают, что сила сопротивления зависит от скорости движения тела, от геометрической формы тела, его линейных размеров, состояния поверхности тела и вязкости среды.
Сила сопротивления среды f наиболее просто может быть определена для тела сферической формы (шарика), движущегося под действием силы тяжести в покоящейся жидкости. Теоретические расчеты, выполненные Стоксом, приводят к выражению:
где
- коэффициент вязкости жидкости;
-
диаметр шарика;
- скорость движения
шарика;
На шарик, падающий
в жидкость, действует сила тяжести
и выталкивающая сила
равная весу жидкости в объёме шарика
–
плотность вещества шарика и жидкости
соответственно. Результирующая сила
равна: 
и направлена вниз. Под влиянием ее шарик движется с ускорением, т.е. с увеличением скорости, но с ростом скорости возрастает и сила сопротивления f среды, в которой движется шарик. Основной закон динамики в этом случае запишется так:
,
т.е.:
По мере движения шарик достигает такой скорости, при которой ускорение становится равным нулю, тогда уравнение (4) принимает вид:
В
этом случае шарик движется с постоянной
скоростью
Подставляя значение объема шарика и
решая относительно
,
получаете:
Скорость
равномерного движения
можно определить по наблюдению времени
t прохождения
шариком определенного пути, тогда
формула
принимает вид:
1.5 Описание аппаратуры и метода измерений
На (рис.3) представлен прибор, применяемый для определения коэффициента вязкости методом шарика, падающего в испытуемой жидкости.
Он представляет собой стеклянный цилиндр (2) , укрепленный на деревянной подставке (1). Цилиндр заполнен исследуемой жидкостью (например, трансформаторным маслом, глицерином и т.д.). На внешней поверхности цилиндра имеются две метки (m и n), расположенные на расстоянии (l) друг от друга. Метки представляют собой кольца (3, 4). Верхнее кольцо находится ниже уровня жидкости на 7 – 9 см. Цилиндр снабжен воронкообразной крышкой (6) с двумя отверстиями. В боковое отверстие помещается термометр (7) для измерения температуры жидкости. Диаметр шариков измеряют микрометром или штангенциркулем.
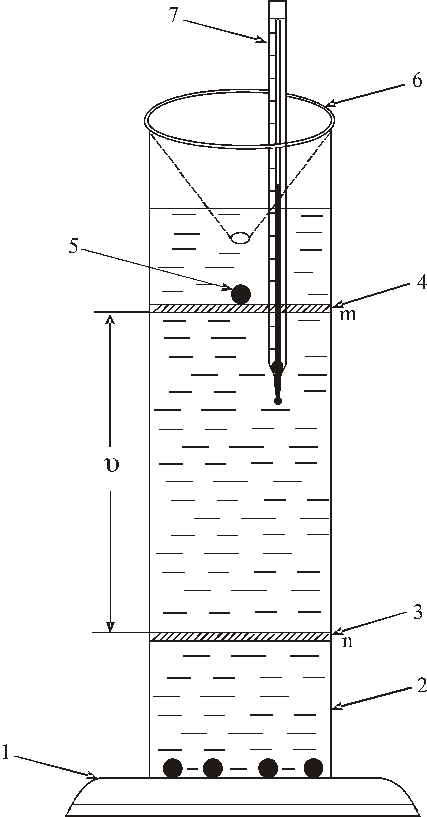
Рис.3. Экспериментальная установка.
1 – деревянная подставка; 2 – стеклянный цилиндр; 3 – нижнее металлическое кольцо; 4 – верхнее подвижное металлическое кольцо; 5 – свинцовый (пластмассовый) шарик; 6 – воронка; 7 – стеклянный термометр