ЛАБОРАТОРНАЯ РАБОТА № 4

ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

Цель работы: экспериментальная проверка уравнения динамики вращательного движения твёрдого тела.

Приборы и оборудование: маятник Обербека, набор грузов, штангенциркуль, сантиметровая линейка, секундомер.

1. Теоретическое введение

1.1. Основной закон вращательного движения

Основное уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси – уравнение моментов – в скалярной форме имеет вид:

, (1)

где – момент импульса тела относительно оси вращения;

– момент инерции тела относительно этой же оси; – его угловая скорость;

– сумма проекций всех моментов сил на ось.

При вращении твёрдого тела его момент инерции не изменяется и уравнение (1) в этом случае принимает простой вид;

или , (2)

где - угловое ускорение твёрдого тела.

Тогда из основного уравнения динамики вращательного движения (2) следует, что угловое ускорение твердого тела прямо пропорционально вращающему моменту при и обратно пропорционально моменту инерции тела при , т.е.

при (3)

при (4)

Проверка этих положений и составляет основную цель данной работы, которую можно осуществить на приборе, называемом крестообразным маятником Обербека.

1.2. Описание аппаратуры и метода измерений

Маятник Обербека представляет собой крестовину (см. рис. 1), состоящую из четырёх стержней длиной и массой , вворачиваемых в лёгкую втулку под углом 90^о друг к другу. Втулка и шкив диаметром D насажены на вал крестовины, опирающийся на подшипники, обеспечивающие вращение с малым трением. На стержни насажены грузы небольших размеров цилиндрической формы с одинаковыми массами и на одинаковых расстояниях R от оси вращения. На обод шкива прикрепляется нить, перекинутая через блок, к свободному концу которой привязывается груз Г массой .

Рис. 1. Маятник Обербека

1- подвешенный груз Г; 2-один из четырёх стержней;

3-один из грузов для стержней; 4-нить; 5-линейка.

Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение. Такая конструкция прибора позволяет изменять момент инерции маятника путем перемещения грузов вдоль стержней и вращающий момент, подвешивая разные грузы Г.

1.3. Вывод расчетных формул

В данной лабораторной работе на шкив действуют два момента силы: момент силы натяжения нити и момент силы трения качения в оси блока. Суммарный момент в проекции на ось равен:

. (5)

Момент, создаваемый силой натяжения нити , имеет вид:

. (6)

Из уравнения движения груза Г находим силу натяжения нити:

или , (7)

где - масса груза Г. Измеряя время , в течение которого груз Г из состояния покоя опустится на расстояние , находим его линейное ускорение по формуле кинематики:

. (8)

Решая совместную систему уравнений (6), (7) и (8), получим выражение для момента :

. (9)

Линейное ускорение точек обода шкива равно линейному ускорению груза Г (нить считаем нерастяжимой). Угловое ускорение шкива связано с линейным ускорением кинематическим соотношением:

. (10)

Подставляя (8) в (10), получим:

. (11)

Итак, момент силы натяжения нити и угловое ускорение маятника можно определить экспериментально, для чего необходимо измерить диаметр шкива , массу груза Г, путь его движения вниз и время движения . Подставляя полученные значения в рабочие формулы (9) и (11), можно проверить выполнение положений (3) и (4).

Экспериментальные данные можно представить графиком зависимости .

В реальном эксперименте момент силы трения исключить невозможно. При небольших нагрузках на ось вращения (при небольшой массе ) момент силы трения можно считать постоянным . В этом случае линейная зависимость от не нарушается.

График позволяет определить момент инерции маятника по наклону графика и момент силы трения . Действительно, из уравнений (2) и (5) имеем:

. (12)

Следовательно, при экспериментальное значение момента инерции маятника можно определить по графику из соотношения:

. (13)

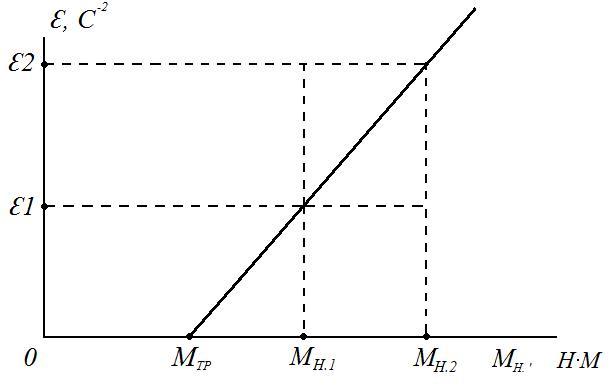
Рис. 2. График

Т.к. при угловое ускорение маятника равно нулю, то момент равен отрезку, отсекаемому графиком на оси _. Определённый по (13) момент инерции маятника можно сравнить с вычисленным значением момента инерции по формуле:

. (14)

Формула (14) записана в предположениях, что момент инерции маятника без стержней пренебрежимо мал и грузы рассматриваются как материальные точки.