ЛАБОРАТОРНАЯ РАБОТА № 3

Определение модуля юнга методом изгиба

Цель работы: изучение упругих деформаций и определение модуля упругости различных материалов.

Приборы и оборудование: установка Гука с набором грузов, штангенциркуль, миллиметровая линейка, индикатор, исследуемые образцы.

1. Теоретическая часть

1.1. Деформации и их характеристики

Деформацией называют всякое изменение в расположении частиц твердого тела, возникающее под действием внешней силы.

Дословно «деформация» означает изменение формы. Однако этот процесс обычно сопровождается и изменением объема тела. В случае малых деформаций любую деформацию можно представить как результат двух слагаемых деформаций.

1. Деформация объема (меняет объем, но форма остается неизменной), например, равномерное всестороннее сжатие однородного шара;

2. Деформация формы (меняется форма, но сохраняется постоянный объем), например, сдвиг верхнего основания куба относительно нижнего, обращающий куб в параллелепипед с тем, же основанием и стой, же высотой, что была у куба.

Всякая деформация в упругом теле сопровождается возникновением внутренних напряжений. Под напряжением р понимают величину силы, действующей на единицу площади поверхности, т.е.:

Процесс деформации в твердом теле сопровождается сложными внутренними изменениями, которые схематически могут быть представлены тремя стадиями: упругая деформация, пластическая деформация, разрушение тела.

Упругая деформация наблюдается при небольшой деформирующей силе, когда величина деформации пропорциональна силе, и по прекращении действия силы исчезает (тело восстанавливает прежнюю форму).

На рис.1 изображена связь между напряжением (деформирующей силой) и величиной деформации. Участок ОА кривой изображает упругую деформацию тела. Этот участок представляет собой прямолинейный отрезок. При дальнейшем увеличении деформирующей силы пропорциональность между деформацией и действующей силой нарушается (деформация растет быстрее, чем действующая сила). На графике эта стадия изображена участком АВ.

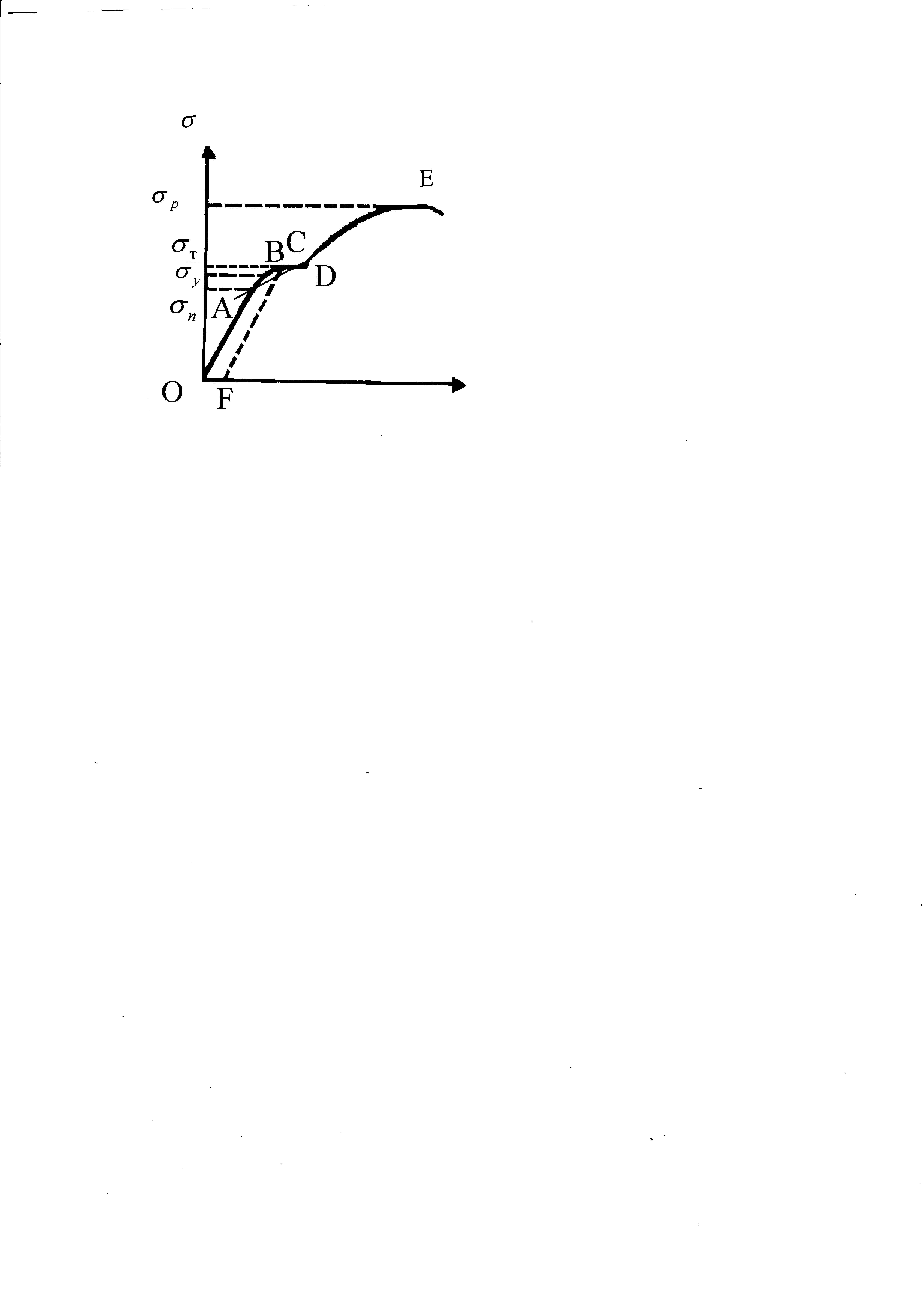
Рис.1. Диаграмма напряжений.

Внутренние напряжения, возникающие в теле в этой стадии, переходят за предел упругости, изображенный на графике ординатой . После прекращения действия силы тело сохраняет остаточную деформацию, т.е. не восстанавливает прежние размеры. Возвращение тела к первоначальному состоянию происходит не по кривой ВАО, а по прямой ВF.

Отрезок ОF и есть остаточная деформация. При последующем увеличении деформирующей силы внутренние напряжения, возникающие в теле под ее действием, переходят за пределы прочности, и наступает разрушение образца. Графически предел прочности изображается ординатой точки Е кривой, начиная с которой касательная к ней становится параллельной оси абсцисс.

Упругая деформация подчиняется закону Гука:

(1)

где  - величина деформации, – коэффициент деформации, F - действующая сила, которая одновременно определяет и величину внутреннего напряжения в теле.

Величина обратная коэффициенту деформации называется модулем упругости.

Коэффициентом деформации называют физическую величину, численно равную деформации, вызванной единичной деформирующей силой.

Модуль деформации определяет величину напряжения, вызывающего относительную деформацию, равную единице.

Если - напряжение, - абсолютная величина деформации (удлинение), - относительное удлинение, тогда , откуда

(2)

Отсюда следует, что модуль упругости равен отношению напряжения к относительному удлинению .