
- •Примеры:
- •Лемма. Образ и ядро линейного оператора φ являются соответственно подпространствами w и V.
- •Вычисление собственных векторов через главные миноры
- •Билинейные функции.
- •Афинное система координат.
- •Линии и поверхности.
- •Аффинная класификация кривых и поврехностей 2-го порядка.
- •Линейные преобразования унитарного простарнства.
- •Комплексификация евклидова пространства.
- •Ортогональная классификация кривых и поверхностей 2-го порядка.
Комплексификация евклидова пространства.
Пусть дано евклидово пространство V.
Рассмотрим V’={z=x+iy,
x,y![]() V}.
V}.
Легко доказывается, что это линейного пространство.
Введем в данном пространтсве следующую операцию ’ такую, что φ’=φx+iφy. Также легко устанавливается, что это линейное преобразование.
Скалярное произведение в V’ будем вычислять следующим образом
(x+iy,u+iv)=(x,u)+(y,v)+i(y,u)-i(x,v)
Все аксиомы скалярного произведения выполняются. Проверим например 4 аксиому
(x+iy,x+iy)=(x,x)+(y,y)+i(x,y)-i(x,y)=(x,x)+(y,y)>0
Лемма. (φ’)![]() =(φ
=(φ![]() )’
)’
Д-во: (φ’z,w)=(φx+iφy,w)=(φx,u)+(φy,v)+i(φy,u)-i(φx,v)
(z,(φ![]() )’w)=(z,(φ
)’w)=(z,(φ![]() )’(u+iv))=(x+iy,φ
)’(u+iv))=(x+iy,φ![]() u+iφ
u+iφ![]() v)=(x,φ
v)=(x,φ![]() u)+(y,φ
u)+(y,φ![]() v)+i(y,φ
v)+i(y,φ![]() u)-i(x,φ
u)-i(x,φ![]() v)=
v)=
=(φx,u)+(φy,v)+i(φy,u)-i(φx,v)
Теорема. Если φ –нормальное (ортогональное, симметричное), то φ’ – нормальное (унитарное, самосопряженное).
Теорема. Преобразование
φ нормальное тогда и только тогда, когда
существует ортонормированнный базис
![]() ,
в котором матрица преобразование будет
блочно-диагональной, причем блоки -
1-ого или 2-ого порядка, где блоки
2-ого порядка имеют следующий вид
,
в котором матрица преобразование будет
блочно-диагональной, причем блоки -
1-ого или 2-ого порядка, где блоки
2-ого порядка имеют следующий вид
![]()
Д-во: <= пусть существует ортонормированный базис, в котором матрица преобразования φ имеет блочно-диагональный вид, т.е.
[φ]=diag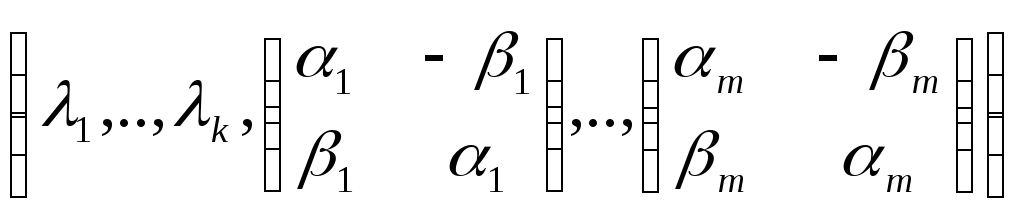
[φ![]() ]=diag
]=diag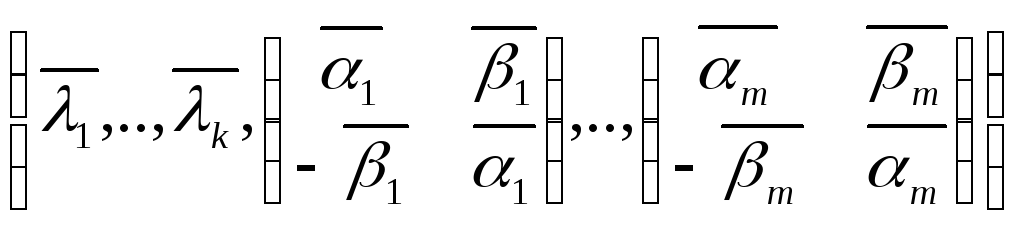
[φ][φ![]() ]=diag
]=diag
Следовательно φφ![]() =φ
=φ![]() φ.
φ.
-
Пусть дано нормальное преобразование φ.
Проведем комплексификацию пространства V. Рассмотрим φ’. Матрица данного преобразовния будет матрица [φ], она нормальная. Поэтому φ’ тоже нормальное.
Рассмотрим
характеристическое уравнение det(φ’-λε)=![]()
Не нарушая общности, можно считать, что система собственных чисел имеет вид:
![]() ,
где λ
,
где λ![]() (i=2s+1,..,n) -
вещественные различные собственные
числа.
(i=2s+1,..,n) -
вещественные различные собственные
числа.
Данной системе будет
соответствовать ортнормированный базис
V’
![]() ,
где вектора f
,
где вектора f![]() (i=2s+1,..,n) – вещественные вектора.
(i=2s+1,..,n) – вещественные вектора.
Рассмотрим комплексные
вектора f![]() и
и
![]()
![]() (i=1,..,s). Пусть f
(i=1,..,s). Пусть f![]() =g
=g![]() +ih
+ih![]() собственный вектор, соответствующий
собственному числу λ
собственный вектор, соответствующий
собственному числу λ![]() =α
=α![]() +iβ
+iβ![]() (β
(β![]() ≠0).
Тогда
≠0).
Тогда
![]()
![]() =g
=g![]() -ih
-ih![]() соответствует собственному числу
α
соответствует собственному числу
α![]() -iβ
-iβ![]()
На ветора f![]() и
и
![]()
![]() натянуто двумерное подпространство:
L(f
натянуто двумерное подпространство:
L(f![]() ,
,
![]()
![]() )=L(g
)=L(g![]() ,h
,h![]() )
)
Отсюда g![]() =(1/2)(f
=(1/2)(f![]() +
+![]()
![]() ),
h
),
h![]() =(-i/2)(f
=(-i/2)(f![]() -
-![]()
![]() ).
Это будут новые базисные вектора.
Нормируем их
).
Это будут новые базисные вектора.
Нормируем их
(g![]() ,
g
,
g![]() )=(1/4)((f
)=(1/4)((f![]() ,
f
,
f![]() )+(
)+(![]()
![]() ,
,![]()
![]() ))=1/2,
(h
))=1/2,
(h![]() ,h
,h![]() )=1/2
)=1/2
Пусть e![]() =
=![]() g
g![]() =
=![]() (
f
(
f![]() +
+![]()
![]() ),
e
),
e![]() =
=![]() h
h![]() =
=![]() (
f
(
f![]() +
+![]()
![]() )
)
Система
![]() и будет ортонормированным базисом.
Вектора будут ортогональны между собой,
потому, что (e
и будет ортонормированным базисом.
Вектора будут ортогональны между собой,
потому, что (e![]() ,
e
,
e![]() )=0,
а остальные равны о из-за ортогональности
прежних векторов.
)=0,
а остальные равны о из-за ортогональности
прежних векторов.
Теперь покажем, что матрица преобразования в данном базисе указанного вида. [φ’]=[φ]
Блоки 1- ого порядка
–это λ
![]() (i=2s+1,..,n) – собственные числа
вещественных собственных векторов.
(i=2s+1,..,n) – собственные числа
вещественных собственных векторов.
Блоки 2-ого порядка. Рассмотрим f=g+ih собственные вектор для числа α+iβ (β≠0)
φ’f=φ’(g+ih)=(α+iβ)(g+ih)=αg-βh+i(αh+βg), но φ’f=φg+iφh
Следовательно φg=αg-βh, φh=αh+βg. Для комплексно сопряженного получаем то же самое.
Т.о. φg![]() =α
=α![]() g
g![]() -β
-β![]() h
h![]() ,
φh
,
φh![]() =β
=β![]() g
g![]() +α
+α![]() h
h![]() .
Умножим на
.
Умножим на
![]() ,
получим
,
получим
φe![]() =α
=α![]() e
e![]() -β
-β![]() e
e![]()
φe![]() =β
=β![]() e
e![]() +α
+α![]() e
e![]()
Отсюда следует, что
блоки 2-ого порядка имеют вида
![]()
Следствие 1. Для
любого ортогонального преобразования
φ евклидова пространства V
существует ортонормированный базис
![]() ,
в котором матрица перобразования имеет
блочно-диагональный вид, причем блоки
1-ого (±1) или 2-ого порядка
,
в котором матрица перобразования имеет
блочно-диагональный вид, причем блоки
1-ого (±1) или 2-ого порядка
![]()
Д-во: φ – ортогональное, значит нормальное. Тогда применим теорему, получим
[φ]=diag
[φ![]() ]=diag
]=diag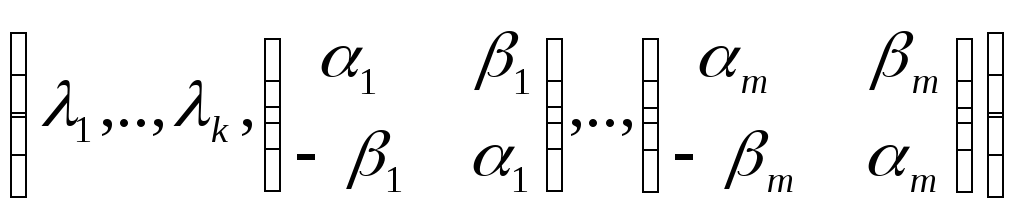
[φ][φ![]() ]=diag
]=diag =E
=E
Блоки 1-ого порядка
λ![]() ²=1
=> λ
²=1
=> λ![]() =±1
=±1
Блоки 2-ого порядка
α![]() ²+β
²+β![]() ²=1.
Решения этого уравнения лежат на
окружности радиуса 1, поэтому если
α
²=1.
Решения этого уравнения лежат на
окружности радиуса 1, поэтому если
α![]() =cosα,
то β
=cosα,
то β![]() =sinα.
=sinα.
Следствие 2. Если φ – симметричное преобразование, то существует ортонормированный базис из собственных векторов.
Д-во: φ – симметричное, значит нормальное. Тогда применим теорему, получаем, что сперва идут собственные числа λ.
-β![]() =β
=β![]() =>
β
=>
β![]() =0
=> α
=0
=> α![]() =λ
=λ![]()
Т. е. по диагонали стоят собственные числа, т.е. ортонормированный базис состоит из собственных векторов.
Следствие
2’. Для любой
вещественной квадратичной формы
существует ортогональное преобразование
x=Qy, при котором x![]() Ax=y
Ax=y![]() Dy=
Dy=![]() .
Это называется приведенение квадратичной
формы к главным осям.
.
Это называется приведенение квадратичной
формы к главным осям.
Д-во: Матрица квадратичной формы симметричная, поэтому по следствию 2 существует ортонормированная матрица перехода Q (от старого к ортонормированному), приводящая матрицу А к диагональному виду, причем по диагонали будут стоять собственные числа.
